算子与线性常微分方程(上)
By 苏剑林 | 2012-11-30 | 37566位读者 | 引用简介
最近在学习量子力学的时候,无意中涉及到了许多矩阵(线性代数)、群论等知识,并且发现其中有不少相同的思想,其中主要是用算子来表示其对函数的作用和反作用。比如我们可以记$D=\frac{d}{dx}$,那么函数$f(x)$的导数就可以看作是算子D对它的一次作用后的结果,二阶导数则是作用了两次,等等。而反过来,$D^{-1}$就表示这个算子的反作用,它把作用后的函数(像)还原为原来的函数(原像),当然,这不是将求导算子做简单的除法,而是积分运算。用这种思想来解答线性微分方程,有着统一和简洁的美。
线性微分方程是求解一切微分方程的基础,一般来说它形式比较简单,多数情况下我们都可以求出它的通解。在非相对论性量子力学的薛定谔方程中,本质上就是在求解一道二阶偏线性微分方程。另一方面,在许多我们无法求解的非线性系统中,线性解作为一级近似,对于定性分析是极其重要的。
一阶线性常微分方程
这是以下所有微分方程求积的一个基础形式,即$\frac{dy}{dx}+g(x)y=f(x)$的求解。这是通过常数变易法来解答的,其思想跟天体力学中的“摄动法”是一致的,首先在无法求解原微分方程的时候,先忽略掉其中的一些小项,求得一个近似解。即我们先求解
$$\frac{dy}{dx}+g(x)y=0$$
算子与线性常微分方程(下)
By 苏剑林 | 2012-11-30 | 19465位读者 | 引用不可交换
很自然会想到把这种方法延伸到变系数微分方程的求解,也许有读者回去自己摆弄了一下却总得不到合适的解而感到困惑。在这里群的非Abel性就体现出来了,首先用一个例子来说明一下,我们考虑算子的复合
$$(D-x)(D+x)=D^2-x^2+(Dx-xD)$$
我们要谨慎使用交换律,我们记$[P,Q]=PQ-QP$
其中P和Q是两个算子,此即量子力学中的“对易式”,用来衡量算子P和算子Q的可交换程度,当然,它本身也是一个算子。我们先来求出$[D,x]$给出了什么(要是它是0的话,那就表明运算可以交换了)。究竟它等于什么呢?直接看是看不出的,我们把它作用于一个函数:
$$[D,x]y=(Dx-xD)y=D(xy)-xDy=yDx+xDy-xDy=y$$
由于“近水楼台先得月”,所以$Dxy$表示x先作用于y,然后D再作用于(xy);而$xDy$表示D先作用于y,然后x再作用于Dy。最终我们得到了
算符的艺术:差分、微分与伯努利数
By 苏剑林 | 2014-10-27 | 34596位读者 | 引用两年前,笔者曾写过《算子与线性常微分方程》两篇,简单介绍了把线形常微分方程算符化,然后通过对算符求逆的方法求得常微分方程的通解。而在这篇文章中,笔者打算介绍关于算符类似的内容:差分算符、微分算符以及与之相关的伯努利数(Bernoulli数)。
我们记$D=\frac{d}{dx}$,那么$Df=\frac{df}{dx}$,同时定义$\Delta_t f(x)=f(x+t)-f(x)$,并且记$\Delta \equiv \Delta_1 =f(x+1)-f(x)$,这里我们研究的$f(x)$,都是具有良好性态的。我们知道,$f(x+t)$在$t=0$附近的泰勒展式为
$$\begin{aligned}f(x+t)&=f(x) + \frac{df(x)}{dx}t + \frac{1}{2!}\frac{d^2 f(x)}{dx^2}t^2 + \frac{1}{3!}\frac{d^3 f(x)}{dx^3}t^3 + \dots\\
&=\left(1+t\frac{d}{dx}+\frac{1}{2!}t^2\frac{d^2}{dx^2}+\dots\right)f(x)\\
&=\left(1+tD+\frac{1}{2!}t^2 D^2+\dots\right)f(x)\end{aligned}$$
线性微分方程组:已知特解求通解
By 苏剑林 | 2014-06-18 | 35495位读者 | 引用含有$n$个一阶常微分方程的一阶常微分方程组
$$\dot{\boldsymbol{x}}=\boldsymbol{A}\boldsymbol{x}$$
其中$\boldsymbol{x}=(x_1(t),\dots,x_n(t))^{T}$为待求函数,而$\boldsymbol{A}=(a_{ij}(t))_{n\times n}$为已知的函数矩阵。现在已知该方程组的$n-1$个线性无关的特解$\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_{n-1}$(解的列向量),求方程的通解。
这是我的一位同学在6月5号问我的一道题目,我当时看了一下,感觉可以通过李对称的方法很容易把解构造出来,当晚就简单分析了一下,发现根据李对称的思想,由上面已知的信息确实足以把通解构造出来。但是我尝试了好几天,尝试了几何、代数等思想,都没有很好地构造出相应的正则变量出来,从而也没有写出它的显式解,于是就搁置下来了。今天再分析这道题目时,竟在无意之间构造出了让我比较满意的解来~
路径积分系列:4.随机微分方程
By 苏剑林 | 2016-06-09 | 25963位读者 | 引用本章将路径积分用于随机微分方程,并且得到了与不对称随机游走一样的结果,从而证明了它与该模型的等价性.
将路径积分用于随机微分方程的研究,这一思路由来已久. 费曼在他的著作[5]中,已经建立了路径积分与线性随机微分方程的关系. 而对于非线性的情况,也有不少研究,但比较混乱,如文献[8]甚至给出了错误的结果.
本文从路径积分的离散化概念出发,明确地建立了两个路径积分微元的雅可比行列式关系,从而对非线性随机微分方程也建立了路径积分. 本文的结果跟文献[9]的结果是一致的.
概念
本文所研究的仅仅是随机常微分方程,它与一般的常微分方程的区别在于布朗运动项的引入,如常见的一类随机微分方程为
$$dx(t)=p(x(t),t)dt + \sqrt{\alpha} dW_t.\tag{48}$$
其中$W_t$代表着一个标准的布朗运动. 由于引入了随机项,所以解$x(t)$不再是确定的,而是有一定的概率分布.
在对随机微分方程中,感兴趣的量有很多,比如关于$x$的某个量的期望、方差,或者稳定性,等等. 随机微分方程领域中有各种分析的技巧,但是显然,直接求出$x(t)$的概率分布后对概率分布进行研究,是最理想最容易的方案. 路径积分正是给出了求概率分布的一个方法.
一阶偏微分方程的特征线法
By 苏剑林 | 2017-12-07 | 74147位读者 | 引用本文以尽可能清晰、简明的方式来介绍了一阶偏微分方程的特征线法。个人认为这是偏微分方程理论中较为简单但事实上又容易让人含糊的一部分内容,因此尝试以自己的文字来做一番介绍。当然,更准确来说其实是笔者自己的备忘。
拟线性情形
一般步骤
考虑偏微分方程
$$\begin{equation}\boldsymbol{\alpha}(\boldsymbol{x},u) \cdot \frac{\partial}{\partial \boldsymbol{x}} u = \beta(\boldsymbol{x},u)\end{equation}$$
其中$\boldsymbol{\alpha}$是一个$n$维向量函数,$\beta$是一个标量函数,$\cdot$是向量的点积,$u\equiv u(\boldsymbol{x})$是$n$元函数,$\boldsymbol{x}$是它的自变量。
力的无穷分解与格林函数法
By 苏剑林 | 2014-11-24 | 32004位读者 | 引用我小时候一直有个疑问:
直升机上的螺旋桨能不能用来挡雨?
一般的螺旋桨是若干个“条状”物通过旋转对称而形成的,也就是说,它并非一个面,按常理来说,它是没办法用来挡雨的。但是,如果在高速旋转的情况下,甚至假设旋转速度可以任意大,那么我们任意时刻都没有办法穿过它了,这种情况下,它似乎与一个实在的面无异?
力的无穷分解
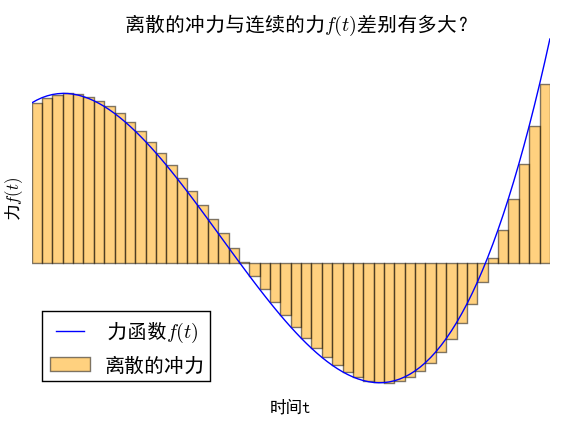
当然,以上只是笔者小时候的一个“异想天开”的念头,读者不必较真。不过,这个疑问跟本文有什么联系呢?我们在研究振动问题之时,通常会遇到在变力的作用下的受迫振动问题,已知变力是时间的函数,比如$f(t)$,然而,虽然知道$f(t)$的具体形式,但是由于$f$的非线性性,加上外力之后的运动,不一定容易求解。然而,如果可以将一个变化的力分段为无数个无穷小时间内的恒力(冲力),那么我们就可以分段讨论我们要研究的运动,而通常来说,恒力的问题会比变力容易。将一个变力离散化,然后再取极限,那么是不是跟原来在变力下的运动是一样的呢?这跟文章开头的疑问有着类似的思想——离线的极限,跟连续本身,是不是等价的?而让人惊喜的是,在通常的物理系统中,将力分段为无数个小区间内的恒力的做法,能够导致正确的答案,而且,这恰好是线性常微分方程的格林函数法。下面我们来分析这一做法。
求解微分方程的李对称方法(一)
By 苏剑林 | 2013-10-29 | 25598位读者 | 引用在这篇日志发表之前,科学空间在整个十月就只是在国庆期间发了一篇小感想,这是比较少见的。一个小原因是这学期社团(广播台)方面的活动有点多,当然这不是主要的,其实这个月我大多数课余时间放到了两件事情上:一是无线电路的入门,二就是本文所要讲的《求解微分方程的李对称方法》。
李对称方法主要是通过发现微分方程的对称性来求解微分方程。我首次接触到这个方法是在一本叫《微分方程与数学物理问题》的书上边,书中写得很清晰易懂,后来我还买了类似的《微分方程的对称与积分方法》,后者相对抽象一些,讨论也深入一些。在我目前发现的中文书籍中,这是唯一的两本以李对称方法求解微分方程为主题的书。这两本书还有一个共同特点,就是它们都是外国教材的翻译版。









最近评论