重温SSM（四）：有理生成函数的新视角

在前三篇文章中，我们较为详细地讨论了HiPPO和S4的大部分数学细节。那么，对于接下来的第四篇文章，大家预期我们会讨论什么工作呢？S5、Mamba乃至Mamba2？都不是。本系列文章主要关心SSM的数学基础，旨在了解SSM的同时也补充自己的数学能力。而在上一篇文章我们简单提过S5和Mamba，S5是S4的简化版，相比S4基本上没有引入新的数学技巧，而Mamba系列虽然表现优异，但它已经将$A$简化为对角矩阵，所用到的数学技巧就更少了，它更多的是体现了工程方面的能力。

这篇文章我们来学习一篇暂时还声名不显的新工作《State-Free Inference of State-Space Models: The Transfer Function Approach》（简称RFT），它提出了一个新方案，将SSM的训练、推理乃至参数化，都彻底转到了生成函数空间中，为SSM的理解和应用开辟了新的视角

基础回顾 #

首先我们简单回顾一下上一篇文章关于S4的探讨结果。S4基于如下线性RNN
$$\begin{equation}\begin{aligned} x_{k+1} =&\, \bar{A} x_k + \bar{B} u_k \\ y_{k+1} =&\, \bar{C}^* x_{k+1} \\ \end{aligned}\label{eq:linear}\end{equation}$$
其中$u,y\in\mathbb{R},x\in\mathbb{R}^d,\bar{A}\in\mathbb{R}^{d\times d},\bar{B},\bar{C}\in\mathbb{R}^{d\times 1}$，这里旨在做一般化的讨论，所以我们绕过了$\bar{A}$与$A$的联系，假设$\bar{A}$为一般矩阵。设初始状态为零，那么直接迭代可以写出：
$$\begin{equation}y_L = \sum_{k=0}^L \bar{C}^*\bar{A}^k \bar{B}u_{L-k} = \bar{K}_{< L} * u_{< L} \end{equation}$$

其中$*$是卷积运算，而
$$\begin{equation}\bar{K}_k = \bar{C}^*\bar{A}^k\bar{B},\quad \bar{K}_{< L} = \big(\bar{K}_0,\bar{K}_1,\cdots,\bar{K}_{L-1}\big),\quad u_{< L} = (u_0,u_1,\cdots,u_{L-1})\end{equation}$$
由于卷积可以通过离散傅里叶变换（DFT）高效计算，所以剩下的问题是如何高效地将$\bar{K}$算出来，这就是S4的核心贡献。为此，S4引入了生成函数
$$\begin{align}\mathcal{G}(z|\bar{K}) =&\, \sum_{k=0}^{\infty} \bar{C}^*\bar{A}^k \bar{B}z^k = \bar{C}^*\left(I - z\bar{A}\right)^{-1}\bar{B} \\ \mathcal{G}_L(z|\bar{K}) =&\, \sum_{k=0}^{L-1} \bar{C}^*\bar{A}^k \bar{B}z^k = \bar{C}^*(I - z^L\bar{A}^L)\left(I - z\bar{A}\right)^{-1}\bar{B} \end{align}$$
如果能够高效地计算$\mathcal{G}_L(z|\bar{K})$，那么就可以代入$z=e^{-2i\pi l/L},l=0,1,2,\dots,L-1$，其结果就是$\bar{K}$的DFT，于是进一步逆变换（IDFT）后就可以得到$\bar{K}$，由于此时的$z$总满足$z^L=1$，所以我们也可以设$\tilde{C}^* = \bar{C}^*(I - \bar{A}^L)$，那么$\mathcal{G}_L(z|\bar{K})$的形式就跟$\mathcal{G}(z|\bar{K})$一致了：
$$\begin{equation}\mathcal{G}_L(z|\bar{K}) = \tilde{C}^*\left(I - z\bar{A}\right)^{-1}\bar{B}\end{equation}$$

那怎么高效计算$\mathcal{G}(z|\bar{K})$或者$\mathcal{G}_L(z|\bar{K})$呢？S4将$\bar{A}$分解为“对角+低秩”的形式，然后通过Woodbury恒等式进行计算，其最终结果为
$$\begin{equation}\mathcal{G}(z|\bar{K}) = \frac{2}{1+z}\bar{C}^* \left[R_z^{-1} - R_z^{-1}u(I + v^*R_z^{-1}u)^{-1} v^*R_z^{-1}\right]B\end{equation}$$
其中$R_z$是$d\times d$的对角阵，$u,v,B,\bar{C}$都是$d\times 1$的列向量，这意味着给定$z$计算$\mathcal{G}(z|\bar{K})$的复杂度为$\mathcal{O}(d)$，而如果要对$z=e^{-2i\pi l/L},l=0,1,2,\dots,L-1$进行计算，那么朴素实现的计算量是$\mathcal{O}(Ld)$。S4提出可以将其转化为Cauchy核问题进行计算，复杂度进一步降低到$\mathcal{O}((L+d)\log^2(L+d))$。

不管哪一种，我们可以发现其复杂度不仅依赖于$L$，还依赖于$d$（state size），而RFT则提出了一种新方法，将复杂度直接降低到了最理想的$\mathcal{O}(L\log L)$，不依赖state size，而且推导过程相比S4还明显简化，同时也不依赖于$\bar{A}$是对角阵或者“对角+低秩”的假设。

有理函数 #

RFT是Rational Transfer Function的缩写，它的重点是Rational Function，即我们所说的有理函数（两个多项式相除）。它跟生成函数有什么关系呢？RFT的作者们非常高明地观察到，$\mathcal{G}_L(z|\bar{K})$实际上是一个有理函数！具体来说，我们有
$$\begin{equation}\mathcal{G}_L(z|\bar{K}) = \tilde{C}^*\left(I - z\bar{A}\right)^{-1}\bar{B} = \frac{b_1 + b_2 z + b_3 z^2 + \cdots + b_dz^{d-1}}{1 + a_1 z + a_2 z^2 + \cdots + a_d z^d}\label{eq:gz-rf}\end{equation}$$
其中$a_1,a_2,\cdots,a_d,b_1,b_2,\cdots,b_d$都是标量，如果$\bar{A},\bar{B},\tilde{C}$都是实矩阵，那么它们都是实数。如果单纯想要意识到存在这么个相等的形式，我们只需要利用矩阵求逆的一个经典公式：
$$\begin{equation}M^{-1} = \frac{\text{adj}(M)}{\det(M)}\end{equation}$$
其中$\det(M)$是$M$的行列式，而$\text{adj}(M)$是$M$的伴随矩阵，由于伴随矩阵涉及到大量行列式计算，所以这个求逆公式在实际计算中通常没什么价值，但在理论分析时通常能起到奇效。比如，我们将它代入到$\mathcal{G}_L(z|\bar{K})$中，就得到
$$\begin{equation}\mathcal{G}_L(z|\bar{K}) = \tilde{C}^*\left(I - z\bar{A}\right)^{-1}\bar{B} = \frac{\tilde{C}^*\text{adj}(I - z\bar{A})\bar{B}}{\det(I - z\bar{A})}\end{equation}$$
我们知道，$d$阶行列式多项$d$个元素相乘的求和，所以$\det(I - z\bar{A})$是关于$z$的$d$次多项式；接着根据伴随矩阵的定义，它的每个元素都是$d-1$阶行列式，也就是$d-1$次多项式，左乘$\tilde{C}^*$和右乘$\bar{B}$只不过是将这些元素加权求和，所以结果还是$d-1$次多项式。因此，$\mathcal{G}_L(z|\bar{K})$是$z$的$d-1$次行列式除以$z$的$d$次行列式，再将分母的常数项系数标准化为$1$，就得到了式$\eqref{eq:gz-rf}$。

对应关系 #

进一步，我们可以利用一个行列式恒等式来确定系数$a=(a_1,a_2,\cdots,a_d),b=(b_1,b_2,\cdots,b_d)$与$\bar{A},\bar{B},\tilde{C}$的关系。这个恒等式是
$$\begin{equation}\det(I + UV) = \det(I + VU)\label{eq:det-iuv}\end{equation}$$
直接证明这个行列式不难，算是一道普通的考研题，只需要注意到
$$\begin{equation}\begin{pmatrix}I & U \\ -V & I\end{pmatrix} = \begin{pmatrix}I + UV & U \\ 0 & I\end{pmatrix}\begin{pmatrix}I & 0 \\ -V & I\end{pmatrix} = \begin{pmatrix}I & 0 \\ -V & I + VU\end{pmatrix}\begin{pmatrix}I & U \\ 0 & I\end{pmatrix}\end{equation}$$
根据行列式的定义和形式，中间部份的行列式就是$\det(I + UV)$，最右边的行列式就是$\det(I + VU)$，它们同一个矩阵的行列式，所以结果相等。这个结果还可以进一步推广到（当$A,D$都可逆时）
$$\begin{equation}\det\begin{pmatrix}A & B \\ C & D\end{pmatrix} = \det(A)\det(D-CA^{-1}B) = \det(D)\det(A-BD^{-1}C)\end{equation}$$
更远一点的话，它还可以一般化为我们在《两个多元正态分布的KL散度、巴氏距离和W距离》提过的“舒尔补（Schur complement）”理论。

回到正题，注意在式$\eqref{eq:det-iuv}$及其推导中，我们不需要假设$U,V$都是方阵，所以实际上式$\eqref{eq:det-iuv}$对于非方阵也是成立的，只要单位阵$I$自动匹配$UV$和$VU$的大小就行。特别地，如果$U,V$分别是列、行向量，那么$VU$就是一个标量，对应的$I$就是1，其行列式就是自身，即$\det(I + UV) = 1 + VU$。利用这个特例，我们有
$$\begin{equation}\begin{aligned} \mathcal{G}_L(z|\bar{K}) =&\, z^{-1}\left[1+\tilde{C}^*\left(z^{-1}I - \bar{A}\right)^{-1}\bar{B} - 1 \right]\\ =&\, z^{-1}\left[\det\left(I + \left(z^{-1} I - \bar{A}\right)^{-1}\bar{B}\tilde{C}^*\right) - 1\right]\\ =&\, z^{-1}\left\{\det\left[\left(z^{-1} I - \bar{A}\right)^{-1}\left(z^{-1} I - \bar{A} + \bar{B}\tilde{C}^*\right)\right] - 1\right\} \\ =&\, z^{-1}\left[\frac{\det(z^{-1} I - \bar{A} + \bar{B}\tilde{C}^*)}{\det(z^{-1} I - \bar{A})} - 1\right] \\ =&\, \frac{z^{d-1}\left[\det(z^{-1} I - \bar{A} + \bar{B}\tilde{C}^*)-\det(z^{-1} I - \bar{A})\right]}{z^d\det(z^{-1} I - \bar{A})} \\ \end{aligned}\end{equation}$$
分母中的$\det(z^{-1} I - \bar{A})$，是以$\lambda=z^{-1}$为变量的矩阵$\bar{A}$的特征多项式，它是$z^{-1}$的$d$次首一多项式，乘以$z^d$后变成了$z$的常数项为1的$d$次多项式；同理，分子中的$\det(z^{-1} I - \bar{A} + \bar{B}\tilde{C}^*)$是$\bar{A} - \bar{B}\tilde{C}^*$的特征多项式（$z^{-1}$的$d$次首一多项式），减去$\det(z^{-1} I - \bar{A})$后正好得到$z^{-1}$的$d-1$次多项式，乘以$z^{d-1}$变成$z$的$d-1$次多项式。所以，$a$向量正好是多项式$\det(\lambda I - \bar{A})$除最高次项外的各系数，而$b$向量则是多项式$\det(\lambda I - \bar{A} + \bar{B}\tilde{C}^*)-\det(\lambda I - \bar{A})$的各系数（次数从高到低排序）。

惊喜突现 #

现在我们先缓一缓，思考一下我们做了什么，要往哪里去。

我们的出发点是线性系统$\eqref{eq:linear}$，为了让它可以并行训练，我们将其转化为了$\bar{K}_{< L}$与$u_{< L}$的卷积，就可以通过先DFT后相乘再IDFT来高效计算，因此这一步的效率不成问题。现在$u_{< L}$是现成的，但$\bar{K}_{< L}$未知，所以问题变成了如何高效计算卷积核$\bar{K}_{< L}=\{\tilde{C}^*\bar{A}^k\bar{B}\}_{k=0}^{L-1}$，为此我们进一步引入了生成函数$\mathcal{G}_L(z|\bar{K})$，只要能够高效计算$\mathcal{G}_L(z|\bar{K})$，那么就有
$$\begin{equation}DFT(\bar{K}_{< L}) = \Big\{\mathcal{G}_L(z|\bar{K})\Big\}_{z=e^{-2i\pi l/L},l=0,1,2,\dots,L-1}\end{equation}$$
然后IDFT就可以恢复原本的$\bar{K}_{< L}$。对于$z=e^{-2i\pi l/L}$，我们有$z^L=1$，于是
$$\begin{equation}\mathcal{G}_L(z|\bar{K}) = \tilde{C}^*(I - z^L\bar{A}^L)\left(I - z\bar{A}\right)^{-1}\bar{B} = \underbrace{\bar{C}^*(I - \bar{A}^L)}_{\tilde{C}^*}\left(I - z\bar{A}\right)^{-1}\bar{B} \end{equation}$$
也就是我们可以先将整个$\bar{C}^*(I - \bar{A}^L)$视为训练参数$\tilde{C}^*$，事后再解出对应的$\bar{C}$用于推理。

S4通过“对角+低秩”的分解来计算$\mathcal{G}_L(z|\bar{K})$，而这篇文章则指出$\mathcal{G}_L(z|\bar{K})$实际上是一个有理函数，即式$\eqref{eq:gz-rf}$。如果我们此时代入$z=e^{-2i\pi l/L}$，就会发现一些让人惊喜的结果，比如分母
$$\begin{equation}1 + a_1 z + a_2 z^2 + \cdots + a_d z^d = \sum_{k=0}^L a_k z^k = \sum_{k=0}^L a_k e^{-2i\pi kl/L} = DFT(\bar{a}_{< L})\end{equation}$$
其中$\bar{a}_{< L} = (a_0,a_1,a_2,\cdots,a_{L-1}) = (1, a_1,a_2, \cdots, a_d, 0, \cdots, 0)$，也就是说，根据定义分母就是将$a$左边拼一个1、后边拼若干个0、凑成$L$个数后的DFT！同理，定义$\bar{b}_{< L} = (b_1,b_2,\cdots,b_d,0,0,\cdots,0)$，那么分子就是$DFT(\bar{b}_{< L})$，于是我们可以简单地写出
$$\begin{equation}DFT(\bar{K}_{< L}) = \frac{DFT(\bar{b}_{< L})}{DFT(\bar{a}_{< L})} = \frac{DFT(b_1,b_2,\cdots,b_d,0,0,\cdots,0)}{DFT(1, a_1,a_2, \cdots, a_d, 0, \cdots, 0)}\end{equation}$$
然后IDFT就可以得到$\bar{K}_{< L}$，其中DFT和IDFT的计算复杂度都是$\mathcal{O}(L\log L)$，跟$d$无关（只需要$d < L$）！这就是RTF的复杂度与state size大小$d$无关的核心思想。

另起炉灶 #

按照上面的引入顺序，我们的计算过程应该是先给定$\bar{A},\bar{B},\tilde{C}$，然后计算$\bar{A}$和$\bar{A}-\bar{B}\tilde{C}^*$的特征多项式系数，进而得到$a_1,a_2, \cdots, a_d$和$b_1,b_2,b_3,\cdots,b_d$，最后计算DFT、相除然后IDFT来得到$\bar{K}_{< L}$。如果是单纯的计算，那么这个过程没啥问题，但我们面对的是训练场景，$\bar{A},\bar{B},\tilde{C}$可能带有训练参数，这时候计算$\bar{A}$和$\bar{A}-\bar{B}\tilde{C}^*$的特征多项式这一步就不那么容易传播梯度了。

对于这个问题，更加干脆的方案是“另起炉灶”——直接以RTF形式的式$\eqref{eq:gz-rf}$为出发点，将$a=(a_1,a_2, \cdots, a_d)$和$b=(b_1,b_2,b_3,\cdots,b_d)$设为可训练参数，那么我们连特征多项式的计算都省了，直接就可以DFT和IDFT去算$\bar{K}_{\leq L}$。不仅如此，原本$\bar{A},\bar{B},\tilde{C}$共有$d^2+2d$个参数，现在$a,b$两个向量一共就$2d$个参数，大大节省了参数量。而因为任意的$\bar{A},\bar{B},\tilde{C}$都可以算出对应的$a,b$，所以RFT的理论能力是不差于原始的RNN形式的。

当然，RTF只是提供了一种直接以$a,b$为参数的高效训练的方式，如果要做step by step推理，那么还是要转回RNN形式，这意味着给定训练好的$a,b$，我们要找出一组$\bar{A},\bar{B},\tilde{C}$，然后代入式$\eqref{eq:linear}$来推理。注意$a,b\to\bar{A},\bar{B},\tilde{C}$是$2d$个参数到$d^2+2d$个参数的映射，肯定有无穷多组解，而我们只需要找出尽可能简单的一组解就行了。

友之矩阵 #

怎么求这组解呢？前面我们已经证明了，$a$向量正好是多项式$\det(z I - \bar{A})$除最高次项外的各系数，所以给定$a$求$\bar{A}$，就是已知特征多项式的情况下求对应的矩阵，最简单的解是对角矩阵，假设$\lambda_1,\lambda_2,\cdots,\lambda_d$为$\lambda^d + a_1 \lambda^{d-1} + a_2 \lambda^{d-2} + \cdots + a_d =0$的$d$个根，那么让$\bar{A}=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_d)$即可。不过，这样可能会出现虚数根，某种程度上可能不够简洁，同时这种纯粹的形式解也无法直接观察$\bar{A}$与$a$之间的联系。

事实上，求一个实矩阵使其特征多项式为给定的实系数多项式，这个问题早有研究，其答案有一个有趣的名字，叫做“友矩阵（Companion matrix）”，其形式为（为了对齐原论文的结果，这里相比维基百科的格式多了个翻转）：
$$\begin{equation}\bar{A} = \begin{pmatrix}-a_1 & - a_2 & \cdots & -a_{d-1} & -a_d \\ 1 & 0 & \cdots & 0 & 0 \\ 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \\ \end{pmatrix}\label{eq:bar-A}\end{equation}$$
事后去证明该矩阵满足
$$\begin{equation}\det(\lambda I-\bar{A})=\lambda^d + a_1 \lambda^{d-1} + a_2 \lambda^{d-2} + \cdots + a_d\end{equation}$$
并不难，直接根据行列式的定义对$\det(\lambda I-\bar{A})$的第一行展开即可。更深刻的问题是如何想到这个构造，这里笔者提供自己的想法。根据特征多项式来构造矩阵，本质上就是逐渐将多项式变换为一个$\lambda$只出现在对角线上的行列式，比如$d=2$时我们有
$$\begin{equation}\lambda^2 + a_1 \lambda + a_2 = (\lambda + a_1)\lambda - (-1) \times a_2 ) = \det\begin{pmatrix} \lambda + a_1 & a_2 \\ -1 & \lambda\end{pmatrix}\end{equation}$$
这就可以抽出对应的$\bar{A}$。对于一般的$d$，我们有
$$\begin{equation}\lambda^d + a_1 \lambda^{d-1} + a_2 \lambda^{d-2} + \cdots + a_d = \det\begin{pmatrix} \lambda^{d-1} + a_1 \lambda^{d-2} + \cdots + a_{d-1} & a_d \\ -1 & \lambda\end{pmatrix}\end{equation}$$
这当然还不是最终答案，但这成功将多项式的次数减少了一，这启示我们或许可以考虑递归地构建，即左上角再以$\lambda^{d-1} + a_1 \lambda^{d-2} + \cdots + a_{d-1}$为特征多项式构造原矩阵，然后微调一下右上和左下的行列，形成分块矩阵。细心多尝试一下，就有机会自己构造出式$\eqref{eq:bar-A}$的结果。

有了$\bar{A}$，构造$\bar{B},\tilde{C}$就容易多了。还是根据前面的结论，我们有
$$\begin{equation}\begin{gathered} \det(\lambda I - \bar{A} + \bar{B}\tilde{C}^*)-\det(\lambda I - \bar{A}) = b_1 \lambda^{d-1} + b_2 \lambda^{d-2} + \cdots + b_d \\ \Downarrow \\ \det(\lambda I - \bar{A} + \bar{B}\tilde{C}^*)= \lambda^d + (a_1 + b_1) \lambda^{d-1} + (a_2+b_2) \lambda^{d-2} + \cdots + (a_d + b_d) \end{gathered}\end{equation}$$
也就是$\bar{A} - \bar{B}\tilde{C}^*$的特征多项式为上式，那么根据$\bar{A}$的构造方式，我们得到$\bar{A} - \bar{B}\tilde{C}^*$的一个解是
$$\begin{equation}\bar{A} - \bar{B}\tilde{C}^* = \begin{pmatrix}-a_1 - b_1 & - a_2 - b_2 & \cdots & -a_{d-1} - b_{d-1} & -a_d - b_d\\ 1 & 0 & \cdots & 0 & 0 \\ 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \\ \end{pmatrix}\end{equation}$$
于是
$$\begin{equation}\bar{B}\tilde{C}^* = \begin{pmatrix}b_1 & b_2 & \cdots & b_{d-1} & b_d\\ 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 0 & 0 \\ \end{pmatrix} = \begin{pmatrix}1 \\ 0 \\ \vdots \\ 0 \\ 0\end{pmatrix}\begin{pmatrix}b_1 & b_2 & \cdots & b_{d-1} & b_d\end{pmatrix}\end{equation}$$
这意味着我们可以找到一组解$\bar{B} = [1, 0, \cdots, 0, 0], \tilde{C}^* = [b_1 , b_2 , \cdots , b_{d-1} , b_d]$，然后进一步解得$\bar{C}^* = \tilde{C}^*(I - \bar{A}^L)^{-1}$。

初始方式 #

我们来完整地$x_k$的递归形式：
$$\begin{equation} x_{k+1} = \begin{pmatrix}-a_1 & - a_2 & \cdots & -a_{d-1} & -a_d \\ 1 & 0 & \cdots & 0 & 0 \\ 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \\ \end{pmatrix} x_k + \begin{pmatrix}1 \\ 0 \\ \vdots \\ 0 \\ 0\end{pmatrix} u_k = \begin{pmatrix} u_k - \langle a, x_k\rangle \\ x_{k,(0)} \\ x_{k,(1)} \\ \vdots \\ x_{k,(d-3)} \\ x_{k,(d-2)}\end{pmatrix} \end{equation}$$
由于$\bar{A}$极其稀疏的特点，每一步递归可以在$\mathcal{O}(d)$而不是$\mathcal{O}(d^2)$完成。特别地，当$a_1=a_2=\cdots=a_d=0$时，我们可以得到：
$$\begin{equation}\begin{aligned} x_1 =&\, [u_0,0,\cdots,0] \\ x_2 =&\, [u_1,u_0,0,\cdots,0] \\ &\vdots \\ x_d =&\, [u_{d-1},\cdots,u_1,u_0] \\ x_{d+1} =&\, [u_d, u_{d-1},\cdots,u_1] \\ &\vdots \\ \end{aligned}\end{equation}$$
也就是说，模型一直在滚动储存最近的$d$个$u_k$，如果没有任何其他先验知识，那么这很明显是一个很合理的初始解，所以原论文在初始化阶段将$a_1,a_2,\cdots,a_d$设为零。

原论文对这个初始化还有一个增强数值稳定性、防止梯度爆炸的解释。从上一篇文章我们知道，线性系统$\eqref{eq:linear}$具备相似不变性，这意味着它的动力学跟将$\bar{A}$对角化后的动力学在数学上是一致的，而$\bar{A}$的对角化矩阵，就是它的特征多项式的所有零点组成的对角矩阵，如果某个零点$\lambda_k$的模大于1，那么经过多步递归后就可能发生数值/梯度爆炸。

换句话说，我们最好可以约束$a_1,a_2,\cdots,a_d$，使得多项式$\lambda^d + a_1 \lambda^{d-1} + a_2 \lambda^{d-2} + \cdots + a_d$的所有零点的模都不大于1，以获得更好的数值稳定性同时避免梯度爆炸。然而，保证多项式的零点都在单位圆内的充要条件依然不得而知，但有一个相对简单的充分条件是$|a_1| + |a_2| + \cdots + |a_d| < 1$。

结论：当$|a_1| + |a_2| + \cdots + |a_d| < 1$时，多项式$\lambda^d + a_1 \lambda^{d-1} + a_2 \lambda^{d-2} + \cdots + a_d$的所有零点模长都不超过1。

证明：用反证法。假设该多项式有一个模大于1的零点$\lambda_0$，那么$|\lambda_0^{-1}| < 1$，于是
$$\begin{equation}\begin{aligned} 1 =&\, -a_1\lambda_0^{-1}-a_2\lambda_0^{-2}-\cdots-a_d \lambda_0^{-d} \\ \leq &\, |a_1\lambda_0^{-1}+a_2\lambda_0^{-2}+\cdots+a_d \lambda_0^{-d}| \\ \leq &\, |a_1\lambda_0^{-1}|+|a_2\lambda_0^{-2}|+\cdots+|a_d \lambda_0^{-d}| \\ \leq &\, |a_1|+|a_2|+\cdots+|a_d| \\ < &\, 1 \end{aligned}\end{equation}$$
这就出现了$1 < 1$的矛盾，因此假设不成立，多项式的所有零点模长都不大于1。

然而，RTF指出，如果直接约束$a_1,a_2,\cdots,a_d$满足$|a_1| + |a_2| + \cdots + |a_d| < 1$，会大大削弱模型的表达能力，弊大于利；RTF进一步发现，只需要在初始化阶段尽可能满足该条件，然后让模型自己慢慢学就行了。最满足这个条件的取值自然是$a_1=a_2=\cdots=a_d=0$，所以RTF选取了全零初始化。

实验效果 #

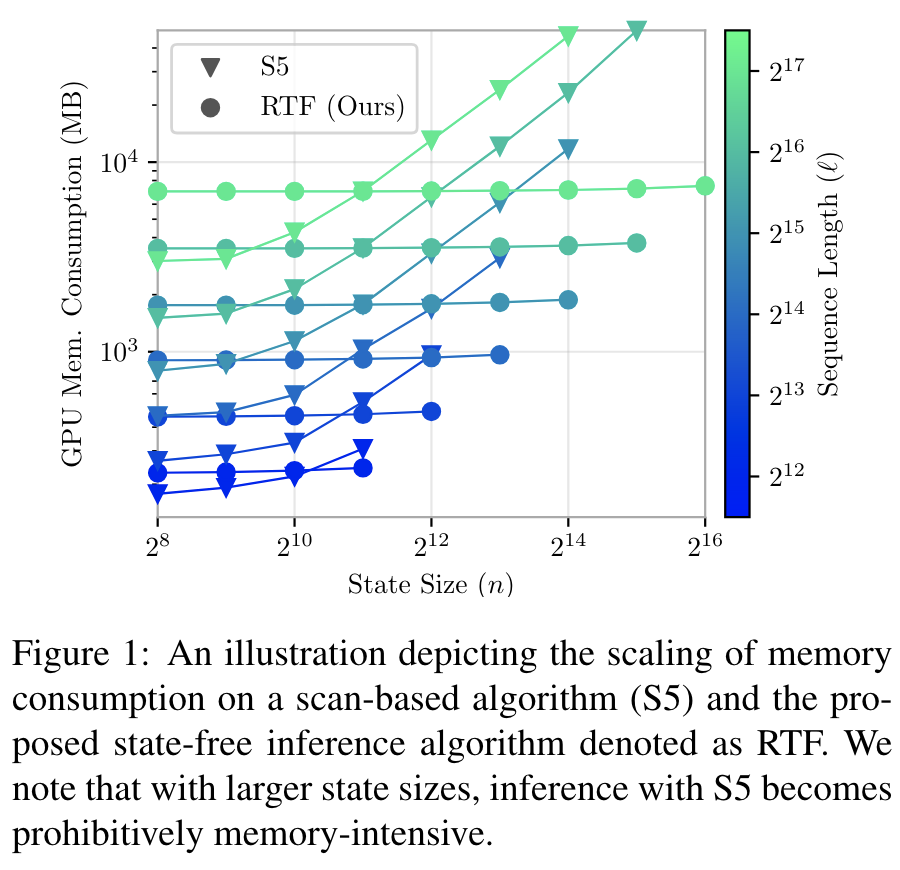
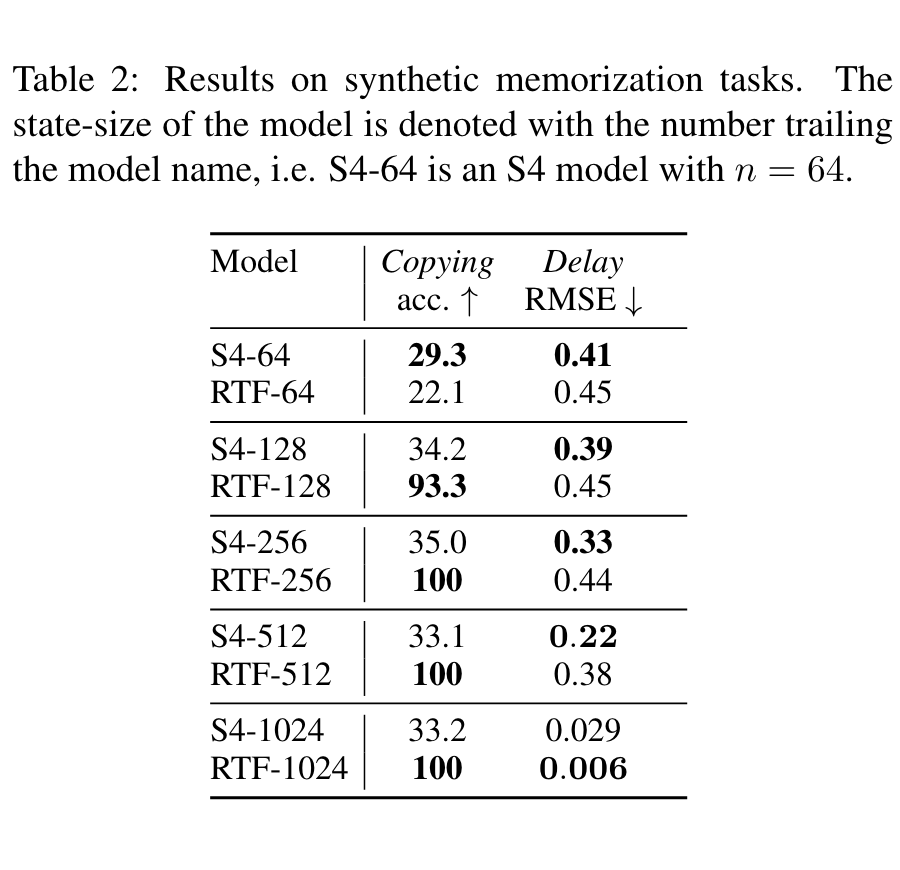
关于实验部份，下面两张图表就可以看出RTF的显著特点：

第一张图显示了RTF的计算复杂度（时间、空间）跟state size没有明显关系，而正因为如此，我们可以通过增大RTF的state size来改善RTF的效果（反正不增加复杂度），也就是第二张图表所显示出来的效果。其他实验结果读者自行翻阅原论文即可。

文章小结 #

本文介绍了SSM模型的一个新工作RTF，它观察到线性RNN的卷积核的生成函数实际上可以表示为一个有理函数（分式多项式），利用这个特点，我们可以将SSM的参数化全部转移到生成函数空间上去，并利用离散傅立叶变换来加速，这使得整个计算流程显著简化。跟S4的“对角+低秩”分解相比，RTF也显得更为简明直观。

转载到请包括本文地址：https://spaces.ac.cn/archives/10180

更详细的转载事宜请参考：《科学空间FAQ》