“闭门造车”之多模态思路浅谈（二）：自回归

这篇文章我们继续来闭门造车，分享一下笔者最近对多模态学习的一些新理解。

在前文《“闭门造车”之多模态思路浅谈（一）：无损输入》中，我们强调了无损输入对于理想的多模型模态的重要性。如果这个观点成立，那么当前基于VQ-VAE、VQ-GAN等将图像离散化的主流思路就存在能力瓶颈，因为只需要简单计算一下信息熵就可以表明离散化必然会有严重的信息损失，所以更有前景或者说更长远的方案应该是输入连续型特征，比如直接将图像的原始像素特征Patchify后输入到模型中。

然而，连续型输入对于图像理解自然简单，但对图像生成来说则引入了额外的困难，因为非离散化无法直接套用文本的自回归框架，多少都要加入一些新内容如扩散，这就引出了本文的主题——如何进行多模态的自回归学习与生成。当然，非离散化只是表面的困难，更艰巨的部份还在后头...

无损含义 #

首先我们再来明确一下无损的含义。无损并不是指整个计算过程中一丁点损失都不能有，这不现实，也不符合我们所理解的深度学习的要义——在2015年的文章《闲聊：神经网络与深度学习》我们就提到过，深度学习成功的关键是信息损失。所以，这里无损的含义很简单，单纯是希望作为模型的输入来说尽可能无损。

当前多模态模型的主流架构依然是Transformer，很多工作都会先对图像进行“前处理”再输入到Transformer中，比如简单将图像Pixels分Patch、通过VAE来提取特征或者通过VQ来离散化等，其共同特点是将图像从$w\times h \times 3$的数组变成$s\times t\times d$（其中$s < w, t < h$）的数组，我们都可以称为广义的“Patchify”。不同的Patchify可能会有不同程度的信息损失，其中VQ的信息损失往往是最严重且最明确的，比如最近字节的TiTok将256*256的图像压缩为32个token，要理解它的信息损失都不用算信息熵，因为它的编码本只有4096，意味着它顶多能存$4096^{32}$张图片，我们知道汉字就不止4096个了，换句话说如果图上有32个汉字，那么所有排列组合就超出了这种编码方式能表达的上限。

如果图像在输入模型之前就有明显信息损失，那么必然会限制模型的图像理解能力，比如将TiTok的32个Token输入到模型中，那么它基本就没法做OCR任务了，而且VQ的这个瓶颈非常本质，即使改为32*32个Token也很难有明显的改善，除非Token的数量达到了原始RGB的Pixels数量级，但这样一来VQ的意义也就没有了。所以，为了更好地适应各种图像理解任务，多模态模型理想的图像输入方式应该就是尽可能无损的连续型特征，由模型自己在计算过程中根据上下文决定要损失什么。

自回归式 #

正如本文开头所说，以连续型特征输入对于图像理解来说其实是一个非常合理和自然的方式，只是对于图像的自回归（AutoRegressive，AR）生成来说会引入额外的困难。看到这里读者可能会有一个疑问：为什么图像非得要做自回归？图像不是有扩散模型这样的更好用的生成方式了吗？

首先，我们知道，“自回归模型 + Teacher Forcing训练”本身就是一种非常普适的学习途径，是“手把手教学”的典型体现，所以它潜力是足够的；其次，扩散模型这个例子，更加说明了自回归在图像生成中的必要性，以DDPM为例，它实质就是一个自回归模型，在《生成扩散模型漫谈（二）：DDPM = 自回归式VAE》我们就将其冠以自回归之名，它将单个图像解构为序列$x_T,x_{T-1},\cdots,x_1,x_0$，然后去建模$p(x_{t-1}|x_t)$，训练方式本质上也是Teacher Forcing（所以也有Exposure Bias问题），可以说DDPM不仅是自回归，而且还只是自回归中最简单的2-gram模型。

事实上，从早期的PixelRNN、PixelCNN、NVAE等工作，到如今流行的扩散模型以及将图像VQ之后当文本那样训练语言模型，它们传递出来的信号更多的是——对于图像来说，问题并不是该不该做自回归，而是以何种方式来更好地去做自回归。它的作用不仅是为多模态模型赋予图像生成能力，而且还是一个重要的无监督学习途径。

笔者的偶像Feynman说过一句著名的话“What I cannot create, I do not understand”，这句话放到大模型也是成立的，也就是说“不会生成就不会理解”。当然，这句话看上去有点武断，因为通过有监督学习各种图文数据对似乎也能获得足够的图像理解能力。然而，单纯通过有监督的方式去学习图像理解，一方面覆盖面可能有限，另一方面也受限于人的理解水平，所以我们需要无监督的生成式预训练来获得更充分的图像理解能力，这跟文本的“Pretrain + SFT”的Pipeline是一致的。

平方误差 #

可能有部份读者觉得，将图像分Patch排序后，不也就可以跟文本一样预测下一个Patch吗？就算输入格式不离散化而是改为连续特征，那也只需要把交叉熵损失换成平方误差就行了？看上去图像的自回归学习也没有什么困难？思路上确实如此，但事实上这里边提到的两个关键地方——“分Patch排序”和“损失函数”——都是难以解决的问题。

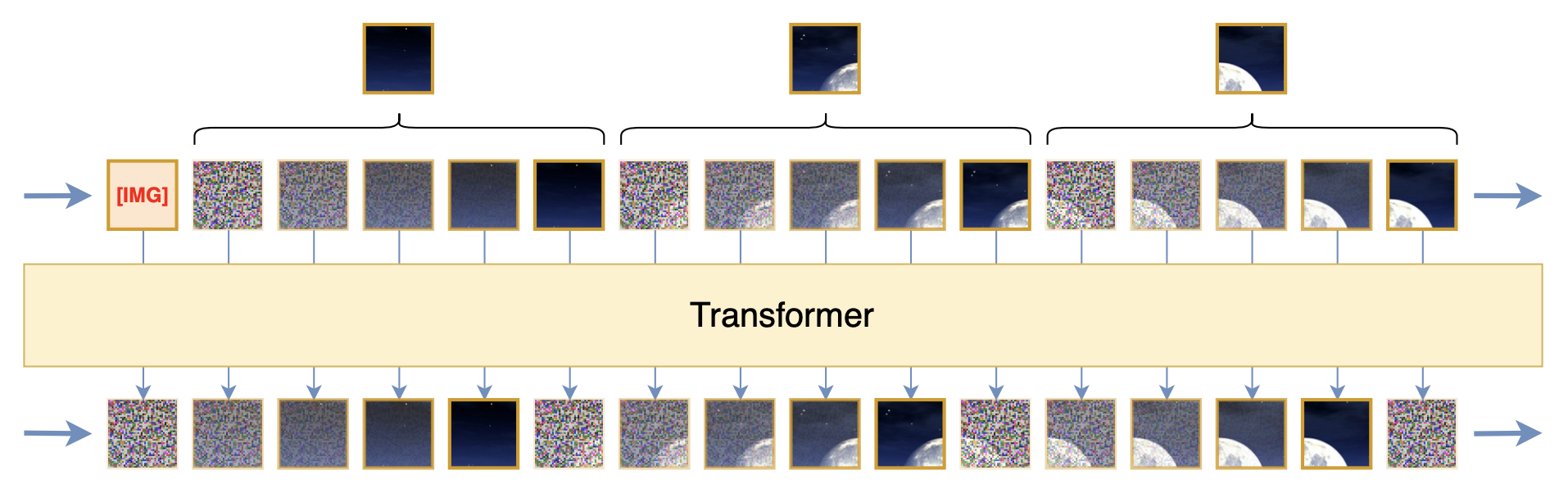
这一节我们先来看损失函数问题。假设图像已经按某种方式分Patch排序好，那么图像就变成了Patch的一维序列，自回归学习也确实是对下一个Patch的预测，如下图所示：

图像自回归学习的最朴素想法是用平方误差预测下一个Patch

然而，这里的损失函数却没法简单地用平方误差（MSE，或者等价地，欧氏距离，L2距离），这是因为平方误差背后的关于分布的假设是高斯分布：
\begin{equation}\frac{1}{2\sigma^2}\Vert x_t - f(x_{< t})\Vert^2 = -\log \mathcal{N}(x_t;f(x_{< t}),\sigma^2) + \text{只依赖}\sigma\text{的常数}\end{equation}
即高斯分布$\mathcal{N}(x_t;f(x_{< t}),\sigma^2)$的负对数似然正好是平方误差（其中$\sigma$是常数），这意味着用平方误差的话对$p(x_t|x_{< t})$的假设为$\mathcal{N}(x_t;f(x_{< t}),\sigma^2)$，但我们仔细想想就会发现，这个假设跟真实情况还是相距甚远的，因为如果它成立，那么通过$x_t = f(x_{< t}) + \sigma\varepsilon$就可以完成$x_t$的采样，其实$\varepsilon$是标准高斯分布的噪声，那么$x_t$必然会有很多噪点，而真实情况显然未必如此。

可能又有读者反驳：为什么非得要从概率似然的角度来理解呢？我就纯粹将它理解为一个回归拟合问题不行吗？可能真的不大行。从概率角度理解主要有两方面的考虑：第一，生成建模最终都要面临采样，写出概率分布才能构建采样方式；第二，单纯从回归的角度来看，我们也需要论证平方误差的合理性，因为我们还有很多其他损失可以用，比如L1距离（MAE）、Hinge Loss等等，这些损失并不相互等价，也不尽合理（事实上，这些损失都不合理，因为它们都是从纯数学角度定义出来的度量，跟人类视觉认知并不完全吻合）。

噪声之奇 #

由于是输入的图片特征本质决定了平方误差的不合理性，所以解决这个问题的唯一思路就是修改图片的输入格式，使得它相应的条件分布更符合高斯分布。目前看来，有两个具体的方案可以参考。

第一个方案是通过预训练的Encoder来编码图片，其中训练Encoder时通常会加入VAE的KL散度等正则项来缩小方差，说得更直观一点，就是将特征都压缩在一个球附近（参考《从几何视角来理解VAE的尝试》），用这些特征作为图像的输入，会使得$p(x_t|x_{< t})$是高斯分布的假设更加合理一些，所以我们可以用平方误差来自回归训练，训练完之后，我们还需要另外训一个Decoder，来将采样出来的图片特征解码为一张图片。这大体上就是Emu2所采用的方案，缺点是Pipeline看起来太长，不够端到端。

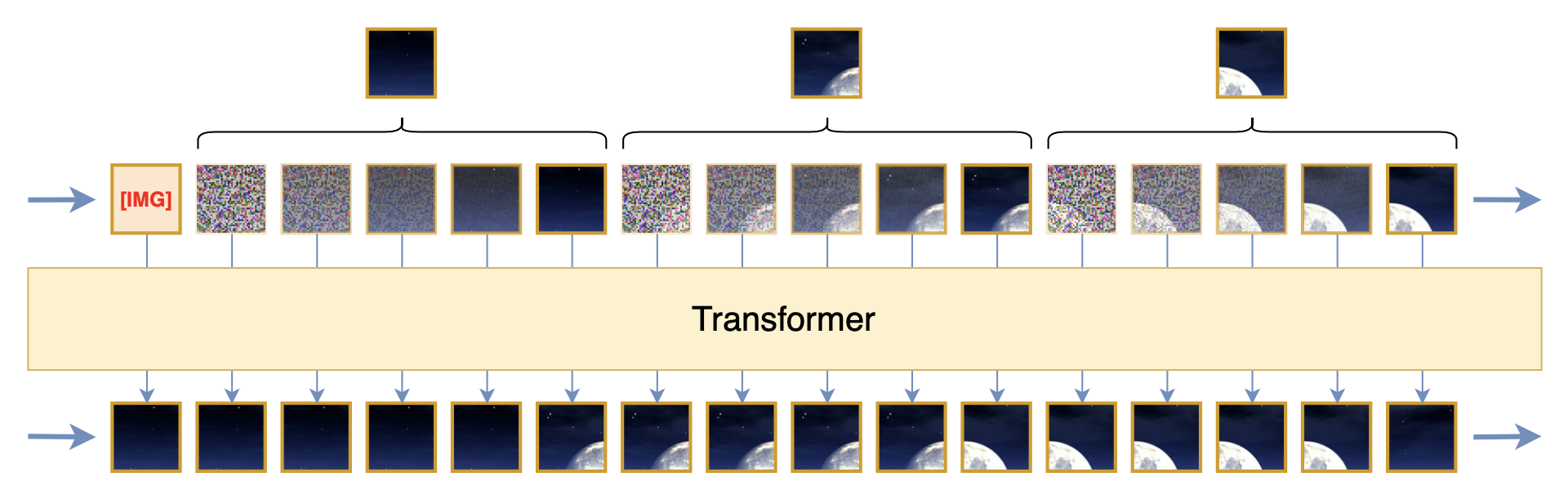
第二个方案可能会出乎很多人意料，那就是加噪，这是笔者闭门造车的想法。刚才我们说如果$p(x_t|x_{< t})$真的是高斯分布，那么直观来看$x_t$应该有很多噪点才对，但事实上没有。那为了满足这个条件，我们自己加一些噪声不就行了？加了噪声也不一定能让$p(x_t|x_{< t})$变成高斯分布，但可以让它更接近，尤其是当我们渐进地加噪声的时候，如下图所示

通过加噪拓展每个Patch，让平方误差成为可行的损失函数

了解扩散模型的读者不难想到，通过加噪来构建渐变序列，然后以平方误差为损失来训练递归去噪模型，这不就是扩散模型吗？没错，扩散模型的核心思想正是“通过渐进式加噪让平方误差成为合理的损失函数”，而上述方案也是借用了这一思想。当然，跟常规扩散模型的不同之处也是很明显的，比如扩散模型是对整张图片加噪，这里是对Patch加噪，扩散模型是建模$p(x_t|x_{t-1})$，这里是建模$p(x_t|x_{< t})$，等等。从最终形式上来看，这里提出的是一种结合扩散模型来进行图像的自回归学习的方案。

效率问题 #

通过加噪来延长序列，使得朴素的平方误差可用，从而让图像的自回归学习跟我们开始构思的方案基本一致（就只是输入多了一步加噪），这无疑是一个非常让人舒适的结果。然而，事情并没有那么乐观，这个方案至少有两大问题，这两个问题也可以概括为同一个词——效率。

第一，是学习效率问题。这个问题我们在第一篇介绍扩散模型的文章《生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼》就已经讨论过了，大致意思就是这种$t-1$时刻的加噪图预测$t$时刻的加噪图的训练目标，需要对噪声进行双重采样，这会导致更大的训练方差，因此需要更多的训练步数才能把这个方差降下来，而经过一系列降方差技巧后，我们发现更高效的方式是直接预测原图（或者等价地，预测它与原图的差）：

相比预测下一步噪声图，直接预测原图效率更高

可能有读者不能理解，刚刚不才说原图没有噪点不符合高斯分布，不能用平方误差为损失吗？这个问题还真不大容易从直观上来解释，我们可以理解为这是高斯分布的一个巧合，这时候平方误差还是可以用的，更标准的解释可以参考《生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪》、《生成扩散模型漫谈（四）：DDIM = 高观点DDPM》这两篇。

第二，是计算效率问题。这个其实很好理解，假如每个Patch通过加噪变成$T$个Patch，那么序列长度就变为原来的$T$倍，这样一来训练成本和推理成本都会显著增加。此外，从理论上来说，加噪的Patch对图像理解并无实质帮助，只保留没加噪的那个干净Patch原则上也能达到同样的效果，换句话说，这种方案对于图像理解来说存在大量冗余的输入和计算量。

解决这个问题同样有两个思路，下面我们逐一介绍。

分离扩散 #

如果限定必须在单个Transformer内解决的话，我们可以考虑给Attention加Mask，这又包括两部分：1、扩散模型的理论和实践告诉我们，要预测$x_t$的话只用$x_{t-1}$就够了，可以忽略更早的输入，这意味同一个Patch的不同加噪结果之间不需要相互Attend；2、出于减少冗余的考虑，对于不同Patch之间的预测以及后面文本Token的预测，我们只需要Attend到没加噪的Patch。这就形成了大致如下的Attention Mask：

出于简化模型和去冗余的考虑所设计的Attention Mask

由于这种Attention Mask具有固定的Sparse Pattern，所以它有很大的提速空间，并且由于带噪的Patch的注意力是独立的，因此我们训练时也不必一次性把$T-1$个带噪Patch都算进去，每次采样一部份计算就行。当然，这顶多只算一个雏形，实践中还有一些细节需要仔细斟酌一下，比如加噪的Patch之间基本没有关联，那么它们的位置编码需要单独设计一下，等等，这里就不展开讨论了。

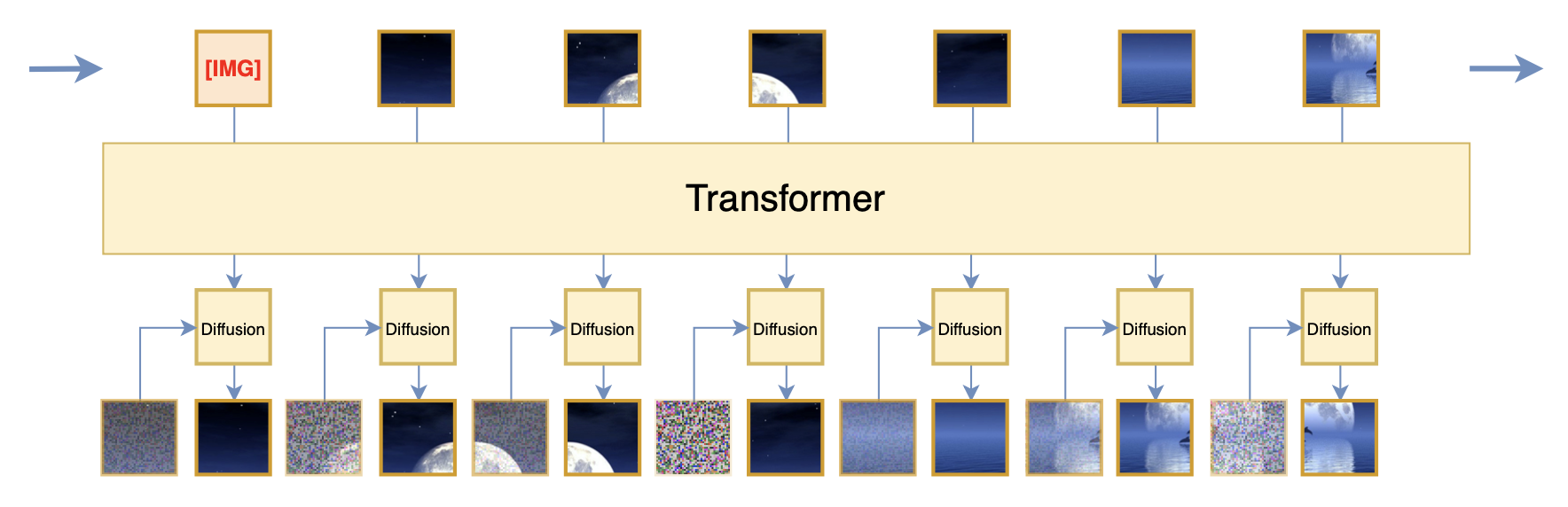
如果允许两个不同的模型串联（但仍然可以端到端训练），那么我们还可以把扩散模型单独分离出来，Transformer只负责处理没有噪声的Patch，Transformer的输出则作为扩散模型的条件，如下图所示：

将扩散模型分离出来，Transformer的输出作为扩散的输入条件

这大体上就是Kaiming的新工作《Autoregressive Image Generation without Vector Quantization》所提的方案，但它更早在《Denoising Autoregressive Representation Learning》就已经被提出，其好处是让Transformer部份更加纯粹和优雅，同时也可以起到节省计算量的作用，这是因为 1)单独分离出来的扩散模型可以做得更小一些； 2)扩散模型部份我们可以按照常规的训练策略每次只采样一个噪声步计算。从损失函数的角度来看，它就是利用了一个额外的扩散模型来作为预测下一个Patch的损失，从而解决平方误差的缺点。

生成方向 #

前面我们提到图像的自回归学习的两个关键之处分别是“分Patch排序”和“损失函数”，刚才我们花了四个小节勉强把损失函数这一块稍微捋顺了一下，但这只能算是刚刚摸到了门槛。然而，接下来我们将会发现一个更让人悲观的结果——对于“分Patch排序”这个问题，我们连门槛都很难摸到。

从最终目标来看，“分Patch排序”是为了给自回归学习制定一个生成序列和方向，它分为“分Patch”和“排序”两步。“分Patch”我们也称“Patchify”，狭义的Patchify就是对像素数组的简单变形和转置，即将$w\times h\times 3$的数组先变形为$s\times (w/s) \times t\times (h/t)\times 3$，然后转置为$s\times t\times (w/s)\times (h/t)\times 3$，最后变形为$s\times t\times (3wh/st)$。但广义来说，Patchify可以泛指一切将图像从$w\times h \times 3$的数组变成$s\times t\times d$（其中$s < w, t < h$）的数组的方案，比如Stable Diffusion的Encoder将图像编码为Latent、各种VQ-Tokenizer将图像变成离散的ID，这些都算是广义的Patchify。

“排序”就比较好理解了，我们知道图像有“长”和“宽”两个方向（维度），大部份Patchify方法的输出特征依然保留了这个二维性质，而自回归生成则是单向的，所以需要指定一个生成顺序。常见的顺序比如 1)从左往右再从上往下 2)从中心到四周螺旋 3)从左上角出发走“Z”字 等等，这些排序设计由来已久，它们可以追溯到第一代图像自回归模型——直接在图像Pixels上做的自回归模型，即前面提到的PixelRNN/PixelCNN等。

朴素的Patchify和两种不同的排序方式

总的来说，“分Patch排序”是将图像解构为一个可供自回归学习的一维序列的过程，更通俗点就是将图像从二维序列转成一维序列，所以从最最广义的角度来讲，扩散模型来构建的不同噪声强度的带噪图片序列，以及《Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction》多个scale构成的序列，都可以归入此列。所以，现在我们已经提到了多种解构图像的方案，那么很自然的问题就是：哪个方案更好？判断依据是什么呢？

世界模型 #

要回答这个问题，我们首先要搞清楚，图像生成或者说视觉生成的本质难度是什么。在《“闭门造车”之多模态思路浅谈（一）：无损输入》中，我们简单提到图像生成的困难在于连续型概率建模的困难，但实际上这是一个非常表面的判断，如果仅仅是这样的话，那么情况就乐观得多了，因为我们已经发展了不少诸如扩散模型的连续型生成模型，但实际上其中的困难比我们想象的更为深远...

我们所说的图像，大体上可以分为人类创造的图片以及相机拍摄的照片两种，在相机、手机普及之后，互联网上的图像实际上已经以照片为主，所以图像生成基本上也等价于照片生成。照片是什么呢？它是光的记录，是三维世界的光在二维平面的投影。那光又是什么呢？光是电磁波，电磁波是麦克斯韦方程组（Maxwell's equations）的解！从这个思考中我们发现一个不可否认的事实：一张真实的自然照片，它本质上就是麦克斯韦方程组的一个解，这也就意味着，完美的图像生成不可避免地要触碰到物理定律——众多理论物理学家孜孜不倦地追求的世界本源！

无独有偶，在Sora出现之后，我们经常会用“是否符合真实世界的物理规律”来评价模型生成的视频质量，实际上看似更加简单图片生成，同样可以有“符合物理规律”这个评价维度，比如图片上的光影分布规律等，只不过到了视频这里，在光学（电磁学）的基础上多了一个动力学。沿着这个思维链头脑风暴下去，会越来越让人觉得震撼甚至惊悚，因为这等价于说完美的视觉生成模型实际上就是在数值模拟各种物理定律，或者更夸张地说，它实际在模拟整个世界、整个宇宙的演化，它本质上就是一个世界模型。这已经不是地狱级难度可以形容的了，这简直就是创世级难度。

可能有读者质疑：麦克斯韦方程组是难，但不也被人类发现了？我们还发现了更多更难的物理规律，比如量子力学、广义相对论等等，并且还在不断逼近终极定律（大统一理论），所以这件事情的难度似乎没有那么高？不，大家不要混淆了，即便我们真的能够发现完全正确的物理定律，那跟有能力“用这些定律去数值模拟”是两回事。比如我们能手写出一个方程，但未必能通过手算去求解它，所以我们能发现物理规律，不代表我们能利用这些物理规律去推演或者模拟真实世界，更具体一点，我们现在能在这里说照片的本质就是麦克斯韦方程组的一个解，但没有谁能够手绘一张照片出来。

（注：以上的一系列思考，起源于“图像本质是麦克斯韦方程组的一个解”，这是在一次技术交流中我的leader周昕宇分享给我的，当我第一次听到这个看上去荒谬但事实上不得不接受的观点时，我内心是错愕且震撼的，霎时间有种明悟了多模态模型的本质困难的感觉。）

人价值观 #

总的来说，这个头脑风暴想要表达的观点就是，一个完美的视觉生成模型，它是一个真正意义上的世界模型，它的难度可谓是创世级别的。那么我们想要创世吗？我们有能力创世吗？笔者认为在可以想象的时间内，答案都是否定的，毕竟那意味着要以人力跟全宇宙对抗的感觉了。所以这里的关键就是放弃“完美”这个概念，就好比人不能手绘出一张照片，但这依然不影响人作画，也不影响人通过手绘的方式来传递信息。又比如说我们评价模型生成的视频是否符合物理规律，并非真的是测量了视频的轨迹然后代入物理公式来判断的，而单纯是肉眼目测加上我们对物理规律的直观感知。

说白了，可以有损，但对人的价值观无损就行了。那这跟前面说的“分Patch排序”又有什么关系呢？我们一开始就说了，自回归学习不单是要为模型赋予生成能力，同时也是作为一种无监督学习途径，来提高模型的理解能力（不会生成就不会理解）。如果我们有一个真正无限拟合能力（创世能力）的模型，那么所有的“分Patch排序”都是等价的，因为精确的联合分布不依赖于随机变量的分解方式。但很遗憾我们没有，那么我们只能有所取舍。

注意，我们希望通过学习生成来促进理解，这里的“理解”必然是要对齐人的视觉理解的，这是我们训练AI的目的。然而，前面列举出来的一些“分Patch排序”方式，没有一种是符合人的视觉理解方式的。更直接地说，人对图片的理解并不是从左往右或者从上往下，也不是从中间到四周还是走“Z”字，甚至说人理解图像都不是按照Patch为单位的，当然也不是Diffusion那样逐渐加噪的方式。如果我们用已有的各种“分Patch排序”方案去做自回归学习，确实有机会赋予模型在一定范围内的视觉生成能力，但由于这些图片解构方式本质上都不符合人的视觉理解模式，那么很难认为这种自回归学习可以促进模型的视觉理解能力——更准确地说，是很难促进模型模仿人视觉理解的能力。

造成这个困难的主要原因，是因为图像它是一个“结果”，并不包含“过程”。就拿人类创作的图像来说，不管是手绘的还是PS的，其过程都是一步一步操作的，但最终呈现出来的是一张掩盖了它创作过程的图像。这跟文字不一样，我们虽然不知道作家是怎么构思出这段文字的，但我们知道大部份人都是从左往右写字的，所以文字本身就已经包含了它的创作（书写）过程，但如果是一幅画呢？看了一幅画，我们知道画家先画哪一块、哪一笔吗？显然不行，这也是为什么大部份人都会写字但无法临摹一幅画。更深一步想，这可以理解为人类似乎更擅长沿着时间维度模仿，而不擅长沿着空间维度，因为时间维度只有一个，空间维度却有三个，后者自由度太大。

目前看来，就只有一个非常“妥协”的方法来解决这个问题，就是用尽可能多的、符合人类价值观的图文数据（当然，图像的其他有价值的监督信号也可以），去有监督地训练一个“分Patch排序”模型。注意跟常见的Vision Encoder不同，这个模型要直接输出一维序列，而不是保留图片的二维性，这样就免去了事后排序这一步。模型的设计我们可以参考TiTok（这是我们第三次提到TiTok了），它本质上是利用Cross Attention将二维序列转一维序列，除此之外用Q-Former也能实现类似的效果。总之，模型设计上不会有太多难度，核心工作变成了图文对的数据工程了。

但这样一来，模型能走多远就不好说了，因为我们本希望通过自回归学习来促进模型的理解能力，但现在自回归学习又依赖于一个通过理解任务训练出来的Encoder，理想情况下这两个模型会相互促进、共同进化，但不理想的情况下模型能力就受限于训练Encoder的有监督数据的数量和质量，无法形成真正的无监督学习了。

文章小结 #

这篇文章继续“闭门造车”了一些有关多模态学习的思路，主要围绕视觉的自回归学习进行展开，大体内容是：

1、自回归学习既为模型赋予了生成能力，同时也是通过生成来促进理解能力的无监督学习途径；

2、对于图像来说，问题不在于要不要做自回归，而是以何种方式才能更好地做自回归；

3、将图像以连续型特征的方式输入时，它的自回归学习有两大难题：分Patch排序和损失函数；

4、损失函数不能简单用平方误差，而是可以考虑后面接一个小型的扩散模型来预测下一个Patch；

5、“分Patch排序”是图像自回归学习的根本难题，它的选择关系到自回归学习能否真正促进理解；

6、完美的图像/视觉生成，不可避免要跟物理规律建立联系，从而构成“世界模型”；

7、但世界模型难以实现，所以选择跟人类价值观相符的“分Patch排序”方式尤为重要；

8、最后，看上去只能“妥协”地通过有监督学习来获得一个对齐人类价值观的“分Patch排序”模型。

这里边可能有不少“暴论”和“谬论”，请读者自行甄别和海涵。将这些思考写下来的主要目的，是为了未来的某一天再回过头来看看，自己当初的想法有几分可行，又有几分可笑。

转载到请包括本文地址：https://spaces.ac.cn/archives/10197

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。