BN究竟起了什么作用?一个闭门造车的分析
By 苏剑林 | 2019-10-11 | 115128位读者 | 引用BN,也就是Batch Normalization,是当前深度学习模型(尤其是视觉相关模型)的一个相当重要的技巧,它能加速训练,甚至有一定的抗过拟合作用,还允许我们用更大的学习率,总的来说颇多好处(前提是你跑得起较大的batch size)。
那BN究竟是怎么起作用呢?早期的解释主要是基于概率分布的,大概意思是将每一层的输入分布都归一化到$\mathcal{N}(0,1)$上,减少了所谓的Internal Covariate Shift,从而稳定乃至加速了训练。这种解释看上去没什么毛病,但细思之下其实有问题的:不管哪一层的输入都不可能严格满足正态分布,从而单纯地将均值方差标准化无法实现标准分布$\mathcal{N}(0,1)$;其次,就算能做到$\mathcal{N}(0,1)$,这种诠释也无法进一步解释其他归一化手段(如Instance Normalization、Layer Normalization)起作用的原因。
在去年的论文《How Does Batch Normalization Help Optimization?》里边,作者明确地提出了上述质疑,否定了原来的一些观点,并提出了自己关于BN的新理解:他们认为BN主要作用是使得整个损失函数的landscape更为平滑,从而使得我们可以更平稳地进行训练。
本博文主要也是分享这篇论文的结论,但论述方法是笔者“闭门造车”地构思的。窃认为原论文的论述过于晦涩了,尤其是数学部分太不好理解,所以本文试图尽可能直观地表达同样观点。
(注:阅读本文之前,请确保你已经清楚知道BN是什么,本文不再重复介绍BN的概念和流程。)
对抗训练浅谈:意义、方法和思考(附Keras实现)
By 苏剑林 | 2020-03-01 | 221755位读者 | 引用当前,说到深度学习中的对抗,一般会有两个含义:一个是生成对抗网络(Generative Adversarial Networks,GAN),代表着一大类先进的生成模型;另一个则是跟对抗攻击、对抗样本相关的领域,它跟GAN相关,但又很不一样,它主要关心的是模型在小扰动下的稳健性。本博客里以前所涉及的对抗话题,都是前一种含义,而今天,我们来聊聊后一种含义中的“对抗训练”。
本文包括如下内容:
1、对抗样本、对抗训练等基本概念的介绍;
2、介绍基于快速梯度上升的对抗训练及其在NLP中的应用;
3、给出了对抗训练的Keras实现(一行代码调用);
4、讨论了对抗训练与梯度惩罚的等价性;
5、基于梯度惩罚,给出了一种对抗训练的直观的几何理解。
无监督分词和句法分析!原来BERT还可以这样用
By 苏剑林 | 2020-06-10 | 83055位读者 | 引用BERT的一般用法就是加载其预训练权重,再接一小部分新层,然后在下游任务上进行finetune,换句话说一般的用法都是有监督训练的。基于这个流程,我们可以做中文的分词、NER甚至句法分析,这些想必大家就算没做过也会有所听闻。但如果说直接从预训练的BERT(不finetune)就可以对句子进行分词,甚至析出其句法结构出来,那应该会让人感觉到意外和有趣了。
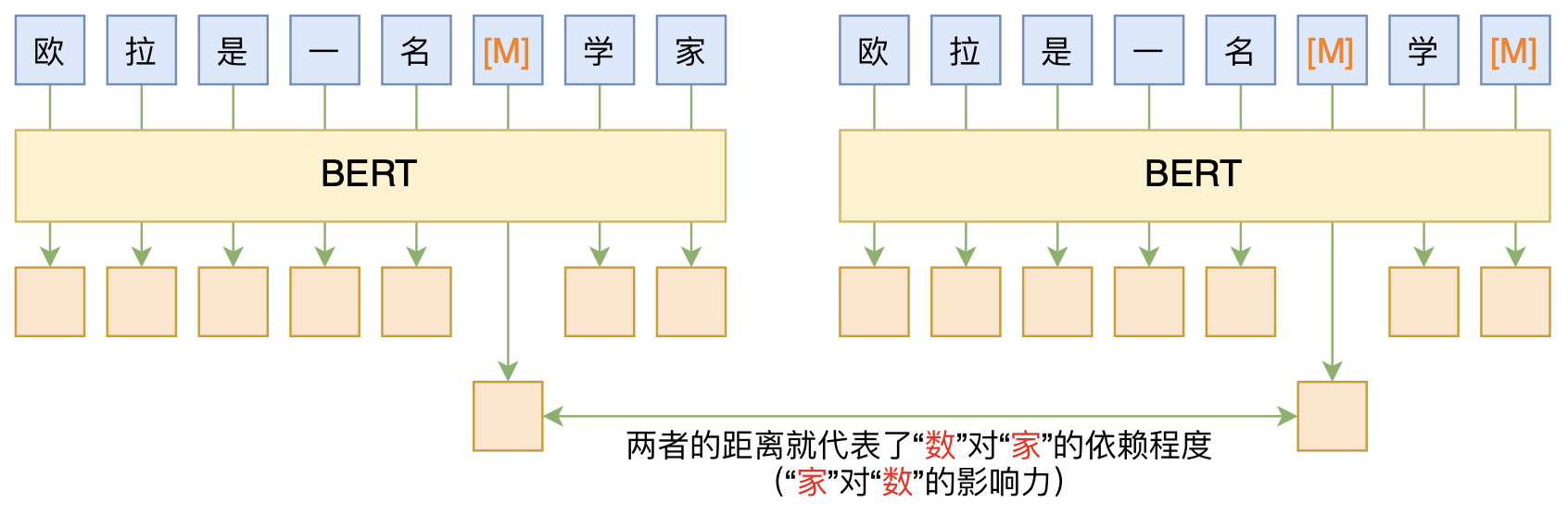
本文介绍ACL 2020的论文《Perturbed Masking: Parameter-free Probing for Analyzing and Interpreting BERT》,里边提供了直接利用Masked Language Model(MLM)来分析和解释BERT的思路,而利用这种思路,我们可以无监督地做到分词甚至句法分析。
L2正则没有想象那么好?可能是“权重尺度偏移”惹的祸
By 苏剑林 | 2020-08-14 | 35161位读者 | 引用L2正则是机器学习常用的一种防止过拟合的方法(应该也是一道经常遇到的面试题)。简单来说,它就是希望权重的模长尽可能小一点,从而能抵御的扰动多一点,最终提高模型的泛化性能。但是读者可能也会发现,L2正则的表现通常没有理论上说的那么好,很多时候加了可能还有负作用。最近的一篇文章《Improve Generalization and Robustness of Neural Networks via Weight Scale Shifting Invariant Regularizations》从“权重尺度偏移”这个角度分析了L2正则的弊端,并提出了新的WEISSI正则项。整个分析过程颇有意思,在这里与大家分享一下。
相关内容
这一节中我们先简单回顾一下L2正则,然后介绍它与权重衰减的联系以及与之相关的AdamW优化器。
L2正则的理解
为什么要添加L2正则?这个问题可能有多个答案。有从Ridge回归角度回答的,有从贝叶斯推断角度回答的,这里给出从扰动敏感性的角度的理解。
Mitchell近似:乘法变为加法,误差不超过1/9
By 苏剑林 | 2020-12-14 | 38300位读者 | 引用今天给大家介绍一篇1962年的论文《Computer Multiplication and Division Using Binary Logarithms》,作者是John N. Mitchell,他在里边提出了一个相当有意思的算法:在二进制下,可以完全通过加法来近似完成两个数的相乘,最大误差不超过1/9。整个算法相当巧妙,更有意思的是它还有着非常简洁的编程实现,让人拍案叫绝。然而,笔者发现网上居然找不到介绍这个算法的网页,所以在此介绍一番。
你以为这只是过时的玩意?那你就错了,前不久才有人利用它发了一篇NeurIPS 2020呢!所以,确定不来了解一下吗?
Transformer升级之路:4、二维位置的旋转式位置编码
By 苏剑林 | 2021-05-10 | 98245位读者 | 引用在之前的文章《Transformer升级之路:2、博采众长的旋转式位置编码》中我们提出了旋转式位置编码RoPE以及对应的Transformer模型RoFormer。由于笔者主要研究的领域还是NLP,所以本来这个事情对于笔者来说已经完了。但是最近一段时间,Transformer模型在视觉领域也大火,各种Vision Transformer(ViT)层出不穷,于是就有了问题:二维情形的RoPE应该是怎样的呢?
咋看上去,这个似乎应该只是一维情形的简单推广,但其中涉及到的推导和理解却远比我们想象中复杂,本文就对此做一个分析,从而深化我们对RoPE的理解。
二维RoPE
什么是二维位置?对应的二维RoPE又是怎样的?它的难度在哪里?在这一节中,我们先简单介绍二维位置,然后直接给出二维RoPE的结果和推导思路,在随后的几节中,我们再详细给出推导过程。
我们可以无损放大一个Transformer模型吗(一)
By 苏剑林 | 2021-06-02 | 56126位读者 | 引用看了标题,可能读者会有疑惑,大家不都想着将大模型缩小吗?怎么你想着将小模型放大了?其实背景是这样的:通常来说更大的模型加更多的数据确实能起得更好的效果,然而算力有限的情况下,从零预训练一个大的模型时间成本太大了,如果还要调试几次参数,那么可能几个月就过去了。
这时候“穷人思维”就冒出来了(土豪可以无视):能否先训练一个同样层数的小模型,然后放大后继续训练?这样一来,预训练后的小模型权重经过放大后,就是大模型一个起点很高的初始化权重,那么大模型阶段的训练步数就可以减少了,从而缩短整体的训练时间。
那么,小模型可以无损地放大为一个大模型吗?本文就来从理论上分析这个问题。
含义
有的读者可能想到:这肯定可以呀,大模型的拟合能力肯定大于小模型呀。的确,从拟合能力角度来看,这件事肯定是可以办到的,但这还不是本文关心的“无损放大”的全部。
WGAN新方案:通过梯度归一化来实现L约束
By 苏剑林 | 2021-11-15 | 53293位读者 | 引用当前,WGAN主流的实现方式包括参数裁剪(Weight Clipping)、谱归一化(Spectral Normalization)、梯度惩罚(Gradient Penalty),本来则来介绍一种新的实现方案:梯度归一化(Gradient Normalization),该方案出自两篇有意思的论文,分别是《Gradient Normalization for Generative Adversarial Networks》和《GraN-GAN: Piecewise Gradient Normalization for Generative Adversarial Networks》。
有意思在什么地方呢?从标题可以看到,这两篇论文应该是高度重合的,甚至应该是同一作者的。但事实上,这是两篇不同团队的、大致是同一时期的论文,一篇中了ICCV,一篇中了WACV,它们基于同样的假设推出了几乎一样的解决方案,内容重合度之高让我一直以为是同一篇论文。果然是巧合无处不在啊~








最近评论