科学空间|Scientific Spaces

转载自2011年1月的《天文爱好者》 作者：薛国轩

“多萝西计划”再探地外文明

据美国空间网站2010年11月13日报道，在人类“探索地外文明”（英文缩写为SETI）50周年纪念之际，世界多个国家的天文学家从本月起再度展开“且听外星人”的联合行动，以延续开始于1960年的“奥兹玛计划”。新的探索活动被命名为“多萝西计划”（Project Dorothy），已于11月5日正式启动，将持续整整一个月时间，来自澳大利亚、日本、韩国、意大利、荷兰、法国、阿根廷和美国的天文学家参与其中。他们将把大大小小的望远镜指向地球周围的一些星球，以期收听到外星人的“天外来音”。

Allen Telescope Array

点击阅读全文...

平面圆形限制性三体问题运动方程及能量积分
plane circular restricted three-body problem
02.04有重要修正！！

寒假一个很大的目标就是能够在三体问题的周期轨道上有点突破，于是就出动了“向量”、“复分析”、“微分方程”等理论“核武”，遗憾的是，“有心栽花花不开”，到今天还是没有多少进展。不过俗语也说“无心插柳柳成荫”，也不错。今天回看《天体力学引论》中的“圆形限制性三体问题”，经过一番思考，利用这些天的思考方法重新推导出了其运动方程和能量积分，也算是“意外收获”在此作为春节礼物与大家分享。

平面圆形限制性三体问题

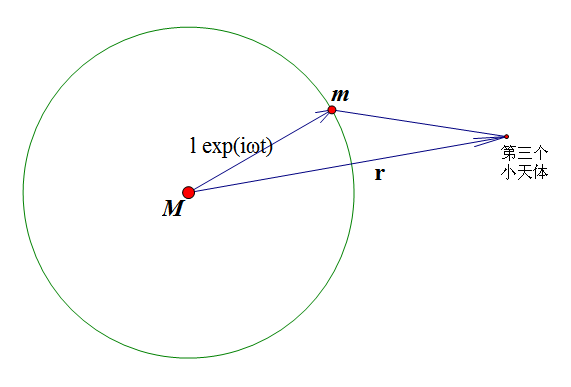
所谓“圆形限制性三体问题”，就是指两个大质量天体（质点）在它们相互引力作用下做圆周运动，假设第三天体（质量趋于0）只受到这两个天体的引力作用而不影响两个天体运行的一种运动情况。由于普通三体问题无法积分，而这个“限制性模型”能够把问题化简不少（不过还是不能积分出来的），因此也得到了一定应用。它的应用条件是：第三体质量小（如当前航天器与地球、太阳）、短程。注意短程也是相当重要的条件之一，注意短程也是相当重要的条件之一，质量越小应用范围越大。要是质量大的话，就不能计算太长的路程。

点击阅读全文...

转载自2011年1月的《天文爱好者》 作者：钟晚晴

生命出现是天体演化的必然结果

探索地外文明

15世纪时，欧洲的文艺复兴运动引起了人们宇宙观的大革命。哥白尼学说的主要传播者之一，意大利思想家布魯诺毫不含糊地宣扬日心说并且提及“外星人”是否存在问题，他这样写到：“宇宙中存在着无数的太阳，存在着无数绕自己太阳运转的地球，就像我们的七个行星绕着我们的太陌运转似的……。在这些世界上居住着各种生物。”科学大师伽利略率先把望远镜指向星空，继而几百年以来有了一系列天文发现。太空视野的大幵阔常引发人类这样的追问：除了地球之外，茫茫宇宙中还存在别的文明星球吗？如果存在，能否找到人类的知音一智慧生命？

科学家通过研究地球化石发现，早在35亿年前地球上就已有了一种发育得比较高级的单细胞生物，即蓝藻类;根据恒星演化理论以及对地球上古老岩石和陨星物质分析知道，太阳和地球的形成比这种生物的出现至少还要早约十几亿年左右。太阳系自原始星云形成后大约经过50亿年地球上才有人类。此外，科学考察表明，在最近五亿年来（根据化石考查）已经有过五次生命大灭绝，人类是五亿年来最后一次灭绝以后从猿进化而来。天体的环境变化往往决定着许许多多生命的命运，例如6500万年前恐龙的绝灭，据说就是遭遇了寒冷的冰期或地球被一颗直径十几千米的小天体撞击的结果。

从20世纪初以来，天文学的研究成果是显著的，例如关于银河系的许多发现，河外星系及宇宙膨胀的发现，特别是后来发现类星体、星际分子、脉冲星、河外星系超新星爆发等等。在进入空间科学和电子计算机科学时代以来，人们对宇宙天体的研究更加深入，每年都有许多新的天体被发现、探究。

点击阅读全文...

在上一些关于限制性三体问题的探讨中，我们得出了在平面上的方程：
$$\ddot{R}+2i\omega \dot{R}=\omega^2 R-GM\frac{R-l_1}{|R-l_1|^3}-Gm\frac{R-l_2}{|R-l_2|^3}\tag{32}$$
能量积分为：
$$\frac{1}{2}|\dot{R}|^2=\frac{1}{2} \omega^2 |R|^2+\frac{GM}{|R-l_1|}+\frac{Gm}{|R-l_2|}-C\tag{33}$$
下面就以这两个方程为基础，再说说限制性三体问题的那些事儿...

点击阅读全文...

假如没有自转，单凭物质之间的引力作用，天体应该都会呈现一个很完美（不是绝对完美）的球形。不过绝大多数的天体都存在着自转，因此他们的赤道半径都比极半径长。BoJone粗糙地考虑了一下在引力和惯性离心力的共同作用下，天体所呈现的形状，并与太阳系的一些天体进行对比，发现还是能够吻合到一定程度。现在此和大家分享，供读者参考。

地球扁率推导

点击阅读全文...

非抛物面望远镜的校正镜方程求解
The Corrector Plate of Non-parabola Telescope

本文在牧夫天文论坛的讨论：
http://www.astronomy.ac/bbs/thread-160257-1-1.html

为了克服折射望远镜的色差问题，1670年，牛顿制造了第一台实用的反射式望远镜，将望远镜的主镜由玻璃透镜换成了抛物反射面，从而消除了色差。然而，相比球面镜，大口径的抛物面并不容易磨制。因为制作大球面镜只需要将曲率相等的小镜片相对自由组合在一起就行了，而抛物线每点的曲率并不相等，所以需要逐个磨制曲率不等的小镜片，并按照严格的顺序组合起来。这无疑大大增加了磨制难度。

Lamost是目前世界最大的施密特望远镜

为了解决这一难题，天文学家们想到了一个折衷的办法：以球面为主镜，并配以校正镜来校正球差。迎着这一思路，施密特望远镜随之而生。而当代的大望远镜基本上都是沿用这一思路。然而，校正镜是一个比抛物面更加复杂的四次曲面，磨制工艺要求更高，因此，校正镜也不宜过大。

点击阅读全文...

月全食-201106160340

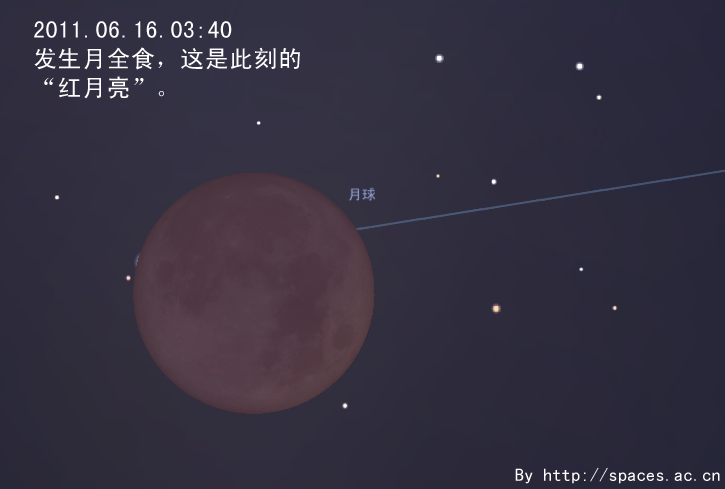
6月中下旬，是北半球一年中黑夜最短的时期。今年6月22日是夏至节气，以北纬40°地区为例，当天天文昏影终到次日天文晨光始的间隔只有不到4小时50分钟。黑夜短暂会使我们可用于天文观测的时间缩短。但在夏至前后，午夜时分太阳也会在地平线下不太低的位置，这样我们就有可能整夜观测到一些类似国际空间站这样的低轨道人造天体。有兴趣的朋友可以查询相关的过境预报，挑战在一晚可以观测到多少次国际空间站过境这类的观测项目。发生在六月的日偏食和月全食，是今年天象的重头戏。接下来笔者就日偏食讲起，跟大家聊聊发生在6月的天象。

点击阅读全文...

通常来说，选取惯性系为参考系，列出的三体问题方程为
$$\ddot{\vec{r}}_k=\sum_{i=1,i != k}^{n} Gm_i\frac{\vec{r}_i-\vec{r}_k}{|\vec{r}_i-\vec{r}_k|^3}$$

历史上出现过很多不同形式的变换，使得三体问题的运动方程有了各样的形式，如Lagrange形式、Jacobi形式、Hamilton形式等。这些变换形式都各有特点，都能够在一定程度上化简三体问题。BoJone在研究摆弄等质量型三体问题的运动方程时，也发现了一种很有趣的变换，在此贴出与大家分享。

设$\vec{R}_1=\vec{r}_1-\vec{r}_2,\vec{R}_2=\vec{r}_2-\vec{r}_3,\vec{R}_3=\vec{r}_3-\vec{r}_1$，则三体问题的运动方程变为

点击阅读全文...