[春礼]《方程与宇宙》:圆形限制性三体问题(七)

平面圆形限制性三体问题运动方程及能量积分
plane circular restricted three-body problem
02.04有重要修正！！

寒假一个很大的目标就是能够在三体问题的周期轨道上有点突破，于是就出动了“向量”、“复分析”、“微分方程”等理论“核武”，遗憾的是，“有心栽花花不开”，到今天还是没有多少进展。不过俗语也说“无心插柳柳成荫”，也不错。今天回看《天体力学引论》中的“圆形限制性三体问题”，经过一番思考，利用这些天的思考方法重新推导出了其运动方程和能量积分，也算是“意外收获”在此作为春节礼物与大家分享。

所谓“圆形限制性三体问题”，就是指两个大质量天体（质点）在它们相互引力作用下做圆周运动，假设第三天体（质量趋于0）只受到这两个天体的引力作用而不影响两个天体运行的一种运动情况。由于普通三体问题无法积分，而这个“限制性模型”能够把问题化简不少（不过还是不能积分出来的），因此也得到了一定应用。它的应用条件是：第三体质量小（如当前航天器与地球、太阳）、短程。注意短程也是相当重要的条件之一，注意短程也是相当重要的条件之一，质量越小应用范围越大。要是质量大的话，就不能计算太长的路程。

本文的研究方法是综合向量、复数以及简单微积分。有关向量的一些拓展可以参看：http://kexue.fm/archives/1188/，要注意的是不要混淆复数的三个乘法运算。主要先研究平面的情况。

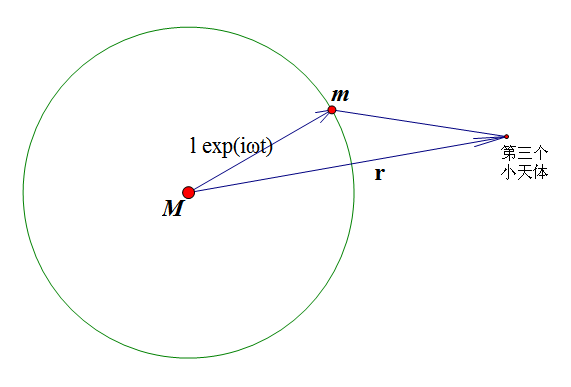
首先，设第三体轨道为$r$，第二体的轨道半径为$l_2$，角速度为$\omega$，质量为m，第一体质量为M，轨道半径为$l_2$，参考点是它们的共同质心，由此得$Ml_1+ml_2=0,|l_1|+|l_2|=l$。选择共同质心而不是任一天体为参考点的原因是共同质心是一个惯性系，才可以进行简单地受力合成。我们可以将第一、二体的运动轨迹表示成$l_1 \exp(i\omega t),l_2 \exp(i\omega t)$（关于$\exp(z)$，有点类似于$e^z$，但又不完全等同。我们依旧有欧拉方程$\exp(i\theta)=\cos\theta+i \sin\theta$，可见这与圆周运动方程的形式是吻合的。），根据受力分析，我们有

$$\ddot{r}=-GM\frac{r-l_1 \exp(i\omega t)}{|r-l_1 \exp(i\omega t)|^3}-Gm\frac{r-l_2 \exp(i\omega t)}{|r-l_2 \exp(i\omega t)|^3}\tag{29}$$
直接用上述方程研究是比较麻烦的，因为右端显含了t。为了想办法消去t，在各项乘以$exp(-i\omega t)$，得：

$$\ddot{r}\exp(-i\omega t)=-GM\frac{r \exp(-i\omega t)-l_1}{|r \exp(-i\omega t)-l_1|^3}-Gm\frac{r \exp(-i\omega t)-l_2}{|r \exp(-i\omega t)-l_2|^3}\tag{30}$$
读者会发现，我们把模长项也乘上了$exp(-i\omega t)$，这是为了统一形式，而且$|exp(-\omega t)=1|$，根据复数乘法的定义，乘上后模长不会改变。

记$R=r exp(-i\omega t)$，可以写出
$$\begin{aligned}\dot{R}=\dot{r}\exp(-i\omega t)-i\omega r \exp(-i\omega t)=\dot{r}\exp(-i\omega t)-i\omega R \\ \ddot{R}=\ddot{r}\exp(-i\omega t)-i\omega dot{r} \exp(-i\omega t)-i\omega \dot{R} \\ =\ddot{r}\exp(-i\omega t)-i\omega(\dot{R}+i\omega R)-i\omega \dot{R} \\ =\ddot{r}\exp(-i\omega t)-2i\omega \dot{R}+\omega^2 R\end{aligned}\tag{31}$$
将(31)代入(30)，得

$$\ddot{R}+2i\omega \dot{R}=\omega^2 R-GM\frac{R-l_1}{|R-l_1|^3}-Gm\frac{R-l_2}{|R-l_2|^3}\tag{32}$$
(32)式就是常用来研究圆形限制性三体问题的微分方程，它不显含t。通过坐标投影可以将其化成直角坐标系形式（三维的也行），还可以设置适当的质量、长度、时间和角度单位，使$G,l,\omega$均为1。大家可能会比较蒙的是那个$l_1,l_2$，之前的定义明明只是一个标量（轨道半径长度），怎么可以跟一个向量减呢？其实，这里的$l_1,l_2$是一个实数，可以看作一个x,y,z分量中y,z均为0的向量。

以上推导用了复数来处理，省去了令人眼花缭乱的坐标变换过程，BoJone认为，这种推导方式能够使大家更容易理解。这种方法的来源得益于这几天对三体周期轨道的思考并将复数与向量进一步融合，使得我对复数更为深刻了。现在继续来推导能量积分。

在(32)式各项“点乘”$\dot{R}$，得
$$\dot{R}\cdot \ddot{R}=\omega^2 R\cdot \dot{R}-GM\frac{(R-l_1)\cdot (R-l_1)'}{|R-l_1|^3}-Gm\frac{(R-l_2)\cdot (R-l_2)'}{|R-l_2|^3}$$

形式在变，恒等不变，恒等式$\vec{r}*\dot{\vec{r}}=|\vec{r}||\vec{r}|'$还是存在的...

$$|\dot{R}||\dot{R}|'=\omega^2 |R||R|'-GM\frac{|R-l_1|'}{|R-l_1|^2}-Gm\frac{|R-l_2|'}{|R-l_2|^2}$$

积分可得
$$\frac{1}{2}|\dot{R}|^2=\frac{1}{2} \omega^2 |R|^2+\frac{GM}{|R-l_1|}+\frac{Gm}{|R-l_2|}-C\tag{33}$$
(33)即能量积分，也称“雅哥比积分”。

注意，$\dot{R}$不是真正的速度，$\dot{r}$才是。我们有
$$\begin{aligned}|\dot{R}|^2=[\dot{r}\exp(-i\omega t)-i\omega r \exp(-i\omega t)]\cdot [\dot{r}\exp(-i\omega t)-i\omega r \exp(-i\omega t)] \\ =[\dot{r}-i\omega r ]\cdot [\dot{r}-i\omega r ]=|\dot{r}|^2+\omega^2 |r|^2-2\omega(ir)\cdot \dot{r}\end{aligned}$$
（请参考复数的点积运算），第二个等号是把两个向量都约去了$exp(-i\omega t)$，意思是都旋转了$\omega t$角，那么其夹角自然没有变，而模长也没有变化，也是点积不变；注意第三个等号中，r是复数，因此还没有确定结果，保留点乘符号“$*$”。而$|R|^2=|r|^2$，代入(33)得

$$\frac{1}{2}|\dot{r}|^2=\frac{GM}{|R-l_1|}+\frac{Gm}{|R-l_2|}+\omega(ir)\cdot \dot{r}-C$$

可见，平面圆形限制性三体问题的能量并非简单地动能和引力势能守恒，它“多出了”$\omega(ir)*\dot{r}$项。
平面圆形限制性三体问题只是一个2维的2阶微分方程，因此它应该要积分出4个常数。上述已经积分出了一个，就剩下三个，不过这三个貌似很难很难...

上述过程只不过是把前人已有的成果重新讲述一次罢了。当然，“讲述”有很多种方式。工作在科学领域前线的专业人士，他们是大多数先进成果的创造者。然而首创的内容（尤其是理论）难免会伴随着“枯燥”。因此，广大的科普工作者更像是一个“翻译家”，他们并不只是把外文翻译成中文，而且要把一些看似高深莫测的科学内容用轻松活泼（至少相对是这样）而又不失严谨的语言描述出来。在BoJone看来，这也是科学松鼠会崛起的原因。BoJone也愿意当这样一位“翻译家”，与各位继续分享科学的美妙。

转载到请包括本文地址：https://spaces.ac.cn/archives/1220

更详细的转载事宜请参考：《科学空间FAQ》