科学空间|Scientific Spaces

众所周知，LoRA是一种常见的参数高效的微调方法，我们在《梯度视角下的LoRA：简介、分析、猜测及推广》做过简单介绍。LoRA利用低秩分解来降低微调参数量，节省微调显存，同时训练好的权重可以合并到原始权重上，推理架构不需要作出改变，是一种训练和推理都比较友好的微调方案。此外，我们在《配置不同的学习率，LoRA还能再涨一点？》还讨论过LoRA的不对称性，指出给$A,B$设置不同的学习率能取得更好的效果，该结论被称为“LoRA+”。

为了进一步提升效果，研究人员还提出了不少其他LoRA变体，如AdaLoRA、rsLoRA、DoRA、PiSSA等，这些改动都有一定道理，但没有特别让人深刻的地方觉。然而，前两天的《LoRA-GA: Low-Rank Adaptation with Gradient Approximation》，却让笔者眼前一亮，仅扫了摘要就有种必然有效的感觉，仔细阅读后更觉得它是至今最精彩的LoRA改进。

究竟怎么个精彩法？LoRA-GA的实际含金量如何？我们一起来学习一下。

点击阅读全文...

在矩阵压缩这个问题上，我们通常有两个策略可以选择，分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸，而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的，那么相应地寻找矩阵稀疏近似的算法又是什么呢？

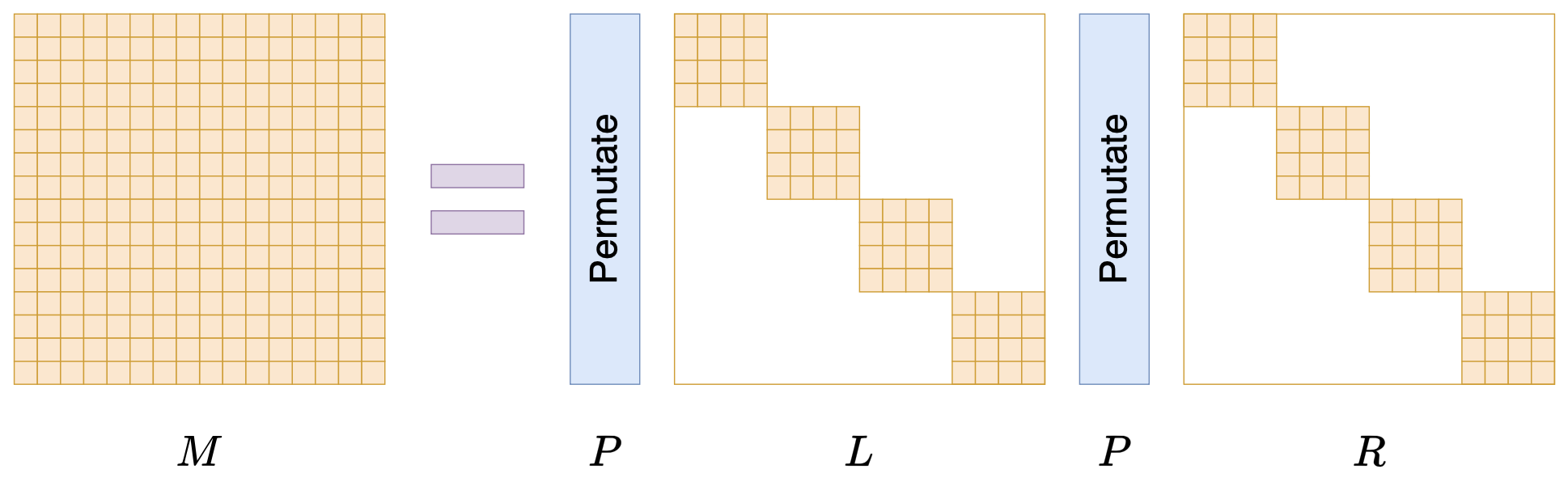
接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》，它为上述问题给出了一个答案——“Monarch矩阵”，这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵，同时具备计算高效且表达能力强的特点，论文还讨论了如何求一般矩阵的Monarch近似，以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。

Monarch矩阵形式M=PLPR

值得指出的是，该论文的作者也正是著名的Flash Attention的作者Tri Dao，其工作几乎都在致力于改进LLM的性能，这篇Monarch也是他主页上特意展示的几篇论文之一，单从这一点看就非常值得学习一番。

点击阅读全文...

当要求函数的最小值时，我们通常会先求导函数然后寻找其零点，比较幸运的情况下，这些零点之一正好是原函数的最小值点。如果是向量函数，则将导数改为梯度并求其零点。当梯度零点不易求得时，我们可以使用梯度下降来逐渐逼近最小值点。

以上这些都是无约束优化的基础结果，相信不少读者都有所了解。然而，本文的主题是概率空间中的优化，即目标函数的输入是一个概率分布，这类目标的优化更为复杂，因为它的搜索空间不再是无约束的，如果我们依旧去求解梯度零点或者执行梯度下降，所得结果未必能保证是一个概率分布。因此，我们需要寻找一种新的分析和计算方法，以确保优化结果能够符合概率分布的特性。

对此，笔者一直以来也感到颇为头疼，所以近来决定”痛定思痛“，针对概率分布的优化问题系统学习了一番，最后将学习所得整理在此，供大家参考。

点击阅读全文...

前两周笔者写了《对齐全量微调！这是我看过最精彩的LoRA（一）》（当时还没有编号“一”），里边介绍了一个名为“LoRA-GA”的LoRA变体，它通过梯度SVD来改进LoRA的初始化，从而实现LoRA与全量微调的对齐。当然，从理论上来讲，这样做也只能尽量对齐第一步更新后的$W_1$，所以当时就有读者提出了“后面的$W_2,W_3,\cdots$不管了吗？”的疑问，当时笔者也没想太深入，就单纯觉得对齐了第一步后，后面的优化也会严格一条较优的轨迹走。

有趣的是，LoRA-GA才出来没多久，arXiv上就新出了《LoRA-Pro: Are Low-Rank Adapters Properly Optimized?》，其所提的LoRA-Pro正好能回答这个问题！LoRA-Pro同样是想着对齐全量微调，但它对齐的是每一步梯度，从而对齐整条优化轨迹，这正好是跟LoRA-GA互补的改进点。

对齐全量

本文接着上一篇文章的记号和内容进行讲述，所以这里仅对上一节的内容做一个简单回顾，不再详细重复介绍。LoRA的参数化方式是
\begin{equation}W = (W_0 - A_0 B_0) + AB\end{equation}

点击阅读全文...

可能很多读者跟笔者一样，对矩阵的低秩近似有种熟悉而又陌生的感觉。熟悉是因为，低秩近似的概念和意义都不难理解，加之目前诸如LoRA等基于低秩近似的微调技术遍地开花，让低秩近似的概念在耳濡目染间就已经深入人心；然而，低秩近似所覆盖的内容非常广，在低秩近似相关的论文中时常能看到一些不熟悉但又让我们叹为观止的新技巧，这就导致了一种似懂非懂的陌生感。

因此，在这个系列文章中，笔者将试图系统梳理一下矩阵低秩近似相关的理论内容，以补全对低秩近似的了解。而在第一篇文章中，我们主要介绍低秩近似系列中相对简单的一个概念——伪逆。

优化视角

伪逆（Pseudo Inverse），也称“广义逆（Generalized Inverse）”，顾名思义就是“广义的逆矩阵”，它实际上是“逆矩阵”的概念对于不可逆矩阵的推广。

点击阅读全文...

Softmax，顾名思义是“soft的max”，是$\max$算子（准确来说是$\text{argmax}$）的光滑近似，它通过指数归一化将任意向量$\boldsymbol{x}\in\mathbb{R}^n$转化为分量非负且和为1的新向量，并允许我们通过温度参数来调节它与$\text{argmax}$（的one hot形式）的近似程度。除了指数归一化外，我们此前在《通向概率分布之路：盘点Softmax及其替代品》也介绍过其他一些能实现相同效果的方案。

我们知道，最大值通常又称Top-1，它的光滑近似方案看起来已经相当成熟，那读者有没有思考过，一般的Top-$k$的光滑近似又是怎么样的呢？下面让我们一起来探讨一下这个问题。

问题描述

设向量$\boldsymbol{x}=(x_1,x_2,\cdots,x_n)\in\mathbb{R}^n$，简单起见我们假设它们两两不相等，即$i\neq j \Leftrightarrow x_i\neq x_j$。记$\Omega_k(\boldsymbol{x})$为$\boldsymbol{x}$最大的$k$个分量的下标集合，即$|\Omega_k(\boldsymbol{x})|=k$以及$\forall i\in \Omega_k(\boldsymbol{x}), j \not\in \Omega_k(\boldsymbol{x})\Rightarrow x_i > x_j$。我们定义Top-$k$算子$\mathcal{T}_k$为$\mathbb{R}^n\mapsto\{0,1\}^n$的映射：
\begin{equation}
[\mathcal{T}_k(\boldsymbol{x})]_i = \left\{\begin{aligned}1,\,\, i\in \Omega_k(\boldsymbol{x}) \\ 0,\,\, i \not\in \Omega_k(\boldsymbol{x})\end{aligned}\right.
\end{equation}
说白了，如果$x_i$属于最大的$k$个元素之一，那么对应的位置变成1，否则变成0，最终结果是一个Multi-Hot向量，比如$\mathcal{T}_2([3,2,1,4]) = [1,0,0,1]$。

点击阅读全文...

在《Cool Papers更新：简单搭建了一个站内检索系统》这篇文章中，我们介绍了Cool Papers新增的站内搜索系统。搜索系统的目的，自然希望能够帮助用户快速找到他们需要的论文。然而，如何高效地检索到对自己有价值的结果，并不是一件简单的事情，这里边往往需要一些技巧，比如精准提炼关键词。

这时候算法的价值就体现出来了，有些步骤人工来做会比较繁琐，但用算法来却很简单。所以接下来，我们将介绍几点通过算法来提高Cool Papers的搜索和筛选论文效率的新尝试。

相关论文

站内搜索背后的技术是全文检索引擎（Full-text Search Engine），简单来说，这就是一个基于关键词匹配的搜索算法，其相似度指标是BM25。

点击阅读全文...

上一篇文章中我们介绍了“伪逆”，它关系到给定矩阵$\boldsymbol{M}$和$\boldsymbol{A}$（或$\boldsymbol{B}$）时优化目标$\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$的最优解。这篇文章我们来关注$\boldsymbol{A},\boldsymbol{B}$都不给出时的最优解，即
\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)$。说白了，这就是要寻找矩阵$\boldsymbol{M}$的“最优$r$秩近似（秩不超过$r$的最优近似）”。而要解决这个问题，就需要请出大名鼎鼎的“SVD（奇异值分解）”了。虽然本系列把伪逆作为开篇，但它的“名声”远不如SVD，听过甚至用过SVD但没听说过伪逆的应该大有人在，包括笔者也是先了解SVD后才看到伪逆。

接下来，我们将围绕着矩阵的最优低秩近似来展开介绍SVD。

结论初探

对于任意矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$，都可以找到如下形式的奇异值分解（SVD，Singular Value Decomposition）：
\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}

点击阅读全文...