科学空间:2010年3月重要天象
By 苏剑林 | 2010-02-28 | 22519位读者 | 引用 3月份,大地回暖,春暖花开了,精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星,火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节,许多有趣、朦胧的深空天体,无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书,新手不妨作为入门的参考书。
3月份,大地回暖,春暖花开了,精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星,火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节,许多有趣、朦胧的深空天体,无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书,新手不妨作为入门的参考书。
梅西叶马拉松是一个自我挑战性相对较强的活动,因为虽然一夜之间所有的梅西耶天体全都亮相,但是因为升起的时间相差很多,有些天体的角度就很低了,并不十分适宜观测,况且一夜之间观测103个天体,即使对星空和器材性能非常熟悉,也需要相当时间(当然啦,你如果有电动赤道仪和导星输入的话,就很简单拉),这会是一个非常辛苦的活动,需要充分准备。 爱好挑战困难者,上吧,探索我们的宇宙!
【问答】为什么绿色星星非常罕见呢?
By 苏剑林 | 2010-02-28 | 28281位读者 | 引用谈大气消光和大气折光
By 苏剑林 | 2010-03-06 | 38526位读者 | 引用苏剑林(BoJone) 编写/翻译
实际感受:
大家也许会有这样的生活经验:早上的太阳没有中午的太阳猛烈?从东方升起到我们的头顶,月亮一直在变“亮”?……这些现象都与地球大气的“消光”现象密切相关!
众所周知,地球有一层厚厚的大气,既是我们呼吸的来源,也是我们生命的保护伞。他为我们提供了臭氧层,也为我们提供了蓝天和风霜雨露,还为我们送上了绚丽的彩虹。然而,在天文学角度,大气却是我们的“障碍”,浓厚的大气不利于我们对宇宙进行清晰的观测。因此,天文学家们一直希望把天文台建立海拔更高的地方,因为那里有着稀薄的大气……为了渴求更高的清晰度,人们甚至把望远镜放到了地球之外。
我们打算飞到小行星上——但是,哪一颗好呢?
By 苏剑林 | 2010-05-01 | 33820位读者 | 引用站长:已经很久没有翻译过科普文章了。现在再来尝试一下,依旧是“Google+金山+搜索+理解”的模式,依旧是那么烂的水平,依旧是那么差的文采,呵呵。有任何意见欢迎提出。 4月15日,美国总统巴拉克·奥巴马视察了位于佛罗里达州的肯尼迪航天中心并发表演讲,提出美国航天新计划:美国未来航天的目的地是火星和小行星,终止布什政府提出的国家载人航天飞行项目。他强有力地回击了其政策的批评者,同时呼吁私营企业铺设飞往火星的创新之路,而不是以国家之力展示美国的优势。 众所周知,载人登小行星比载人登月难多了。除了苛刻的技术条件外,适合登录的小行星也不多,奥巴马的新方案真的可行吗?让我们拭目以待!
奔向固原,追逐梦想...
By 苏剑林 | 2010-05-14 | 49121位读者 | 引用科学空间:2010年6月重要天象
By 苏剑林 | 2010-05-30 | 27845位读者 | 引用进入六月,除除了水星外肉眼可见的几颗大行星观测条件还不错。前半夜的主要观测目标是金星、火星和土星,他们之间的角距离也在逐渐缩小。后半夜木星升起,我们又有机会一睹这颗太阳系内最大行星的风采了。6月21日是夏至节气,当天北半球白昼是一年中最长的,而夜晚最短,且越往北越短。在北极圈以内地区当天太阳将不会落到地平线以下18度之内时,辉光都会影响到我们目视的极限星等,因此夏至前后一段时间北纬50度以上地区不太适合进行天文观测了。而对于北纬30至40度左右的观测者来说,这期间适合开展人造天体,特别是国际空间站的观测活动。
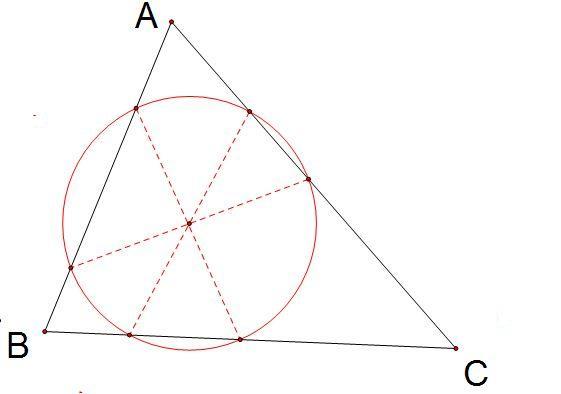
神秘的圆——三角形的“六接圆”(添加新方法)
By 苏剑林 | 2010-07-24 | 31313位读者 | 引用《向量》系列——1.向心力公式证明
By 苏剑林 | 2010-07-15 | 57200位读者 | 引用向量在几何和物理中都有极其重要的作用,现在就让我们来看如何用向量研究物理中的圆周运动。
首先我们必须了解一些基础:
1.在向量中,只要一条“向径”($\vec{r}$)就可以描述出物体的运动,而不需要建立坐标系。这就是向量应用于物理的原因:物理定律不应该依赖于坐标系,而向量恰恰也不依赖于坐标系!
2.牛顿第二定律:$\vec{F}=m\vec{a}$
3.以及一些向量的微积分运算等(可以查阅维基百科或者相关资料)
在下面及以后的文章描述中,为了大家的阅读方便,把向量写成$\vec{r}$的形式,而非把字母加粗。一般情况下,在本站的描述中,有$|\vec{r}|=r,|\dot{\vec{r}}|=v,|\ddot{\vec{r}}|=a$。但是,$\dot{r}=\frac{d|\vec{r}|}{dt} != |\dot{\vec{r}}|$












最近评论