向量在几何和物理中都有极其重要的作用，现在就让我们来看如何用向量研究物理中的圆周运动。

首先我们必须了解一些基础：

1.在向量中，只要一条“向径”($\vec{r}$)就可以描述出物体的运动，而不需要建立坐标系。这就是向量应用于物理的原因：物理定律不应该依赖于坐标系，而向量恰恰也不依赖于坐标系！
2.牛顿第二定律：$\vec{F}=m\vec{a}$
3.以及一些向量的微积分运算等（可以查阅维基百科或者相关资料）

在下面及以后的文章描述中，为了大家的阅读方便，把向量写成$\vec{r}$的形式，而非把字母加粗。一般情况下，在本站的描述中，有$|\vec{r}|=r,|\dot{\vec{r}}|=v,|\ddot{\vec{r}}|=a$。但是，$\dot{r}=\frac{d|\vec{r}|}{dt} != |\dot{\vec{r}}|$

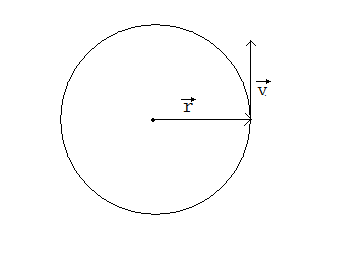
圆周运动示意图

圆周运动示意图

上图是一个简单的圆周运动示意图，其中我们得到：
$$\begin{aligned}\vec{F}=m\vec{a} \\ \vec{a}=\ddot{\vec{r}} \\ \vec{v}=\dot{\vec{r}}\end{aligned}$$

其中$\vec{F}$是合外力，由于速度方向总是与向径方向垂直，我们就有
$$\vec{r}\cdot \dot{\vec{r}}=0\tag{1}$$并且
$$\frac{d}{dt}(\vec{r}\cdot \dot{\vec{r}})=\dot{\vec{r}}^2+\vec{r}\cdot \ddot{\vec{r}}=0$$
得出
$$\begin{aligned}m\dot{\vec{r}}^2+\vec{r}\cdot m\ddot{\vec{r}}=0 \\ mv^2+\vec{r}\cdot \vec{F}=0\end{aligned}\tag{2}$$
其中$\vec{F}$是合外力（请记住，向心力由合外力提供，是合外力的一个分力，不能说物体受到向心力的作用），(1)和(2)结合起来，就是描述圆周运动的基本方程。

如果该运动为匀速圆周运动，v恒定，则应该有$\dot{\vec{r}}^2=const$，即
$$\frac{d}{dt}(\dot{\vec{r}}^2)=2\dot{\vec{r}}\cdot \ddot{\vec{r}}=0$$
即$$\dot{\vec{r}}\cdot \vec{F}=0\tag{3}$$
即合外力方向与速度方向垂直，结合(2)，有
$$\begin{aligned}\vec{F}=-m(\frac{\dot{\vec{r}}^2}{r^2})\vec{r}=-m\omega^2 \vec{r} \\ F=\frac{mv^2}{r}\end{aligned}$$

转载到请包括本文地址：https://spaces.ac.cn/archives/701

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jul. 15, 2010). 《《向量》系列——1.向心力公式证明 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/701

@online{kexuefm-701,
        title={《向量》系列——1.向心力公式证明},
        author={苏剑林},
        year={2010},
        month={Jul},
        url={\url{https://spaces.ac.cn/archives/701}},
}