【中文分词系列】 4. 基于双向LSTM的seq2seq字标注
By 苏剑林 | 2016-08-22 | 460841位读者 | 引用关于字标注法
上一篇文章谈到了分词的字标注法。要注意字标注法是很有潜力的,要不然它也不会在公开测试中取得最优的成绩了。在我看来,字标注法有效有两个主要的原因,第一个原因是它将分词问题变成了一个序列标注问题,而且这个标注是对齐的,也就是输入的字跟输出的标签是一一对应的,这在序列标注中是一个比较成熟的问题;第二个原因是这个标注法实际上已经是一个总结语义规律的过程,以4tag标注为为例,我们知道,“李”字是常用的姓氏,一半作为多字词(人名)的首字,即标记为b;而“想”由于“理想”之类的词语,也有比较高的比例标记为e,这样一来,要是“李想”两字放在一起时,即便原来词表没有“李想”一词,我们也能正确输出be,也就是识别出“李想”为一个词,也正是因为这个原因,即便是常被视为最不精确的HMM模型也能起到不错的效果。
关于标注,还有一个值得讨论的内容,就是标注的数目。常用的是4tag,事实上还有6tag和2tag,而标记分词结果最简单的方法应该是2tag,即标记“切分/不切分”就够了,但效果不好。为什么反而更多数目的tag效果更好呢?因为更多的tag实际上更全面概括了语义规律。比如,用4tag标注,我们能总结出哪些字单字成词、哪些字经常用作开头、哪些字用作末尾,但仅仅用2tag,就只能总结出哪些字经常用作开头,从归纳的角度来看,是不够全面的。但6tag跟4tag比较呢?我觉得不一定更好,6tag的意思是还要总结出哪些字作第二字、第三字,但这个总结角度是不是对的?我觉得,似乎并没有哪些字固定用于第二字或者第三字的,这个规律的总结性比首字和末字的规律弱多了(不过从新词发现的角度来看,6tag更容易发现长词。)。
双向LSTM
【中文分词系列】 2. 基于切分的新词发现
By 苏剑林 | 2016-08-18 | 122761位读者 | 引用上一篇文章讲的是基于词典和AC自动机的快速分词。基于词典的分词有一个明显的优点,就是便于维护,容易适应领域。如果迁移到新的领域,那么只需要添加对应的领域新词,就可以实现较好地分词。当然,好的、适应领域的词典是否容易获得,这还得具体情况具体分析。本文要讨论的就是新词发现这一部分的内容。
这部分内容在去年的文章《新词发现的信息熵方法与实现》已经讨论过了,算法是来源于matrix67的文章《互联网时代的社会语言学:基于SNS的文本数据挖掘》。在那篇文章中,主要利用了三个指标——频数、凝固度(取对数之后就是我们所说的互信息熵)、自由度(边界熵)——来判断一个片段是否成词。如果真的动手去实现过这个算法的话,那么会发现有一系列的难度。首先,为了得到$n$字词,就需要找出$1\sim n$字的切片,然后分别做计算,这对于$n$比较大时,是件痛苦的时间;其次,最最痛苦的事情是边界熵的计算,边界熵要对每一个片段就行分组统计,然后再计算,这个工作量的很大的。本文提供了一种方案,可以使得新词发现的计算量大大降低。
【中文分词系列】 3. 字标注法与HMM模型
By 苏剑林 | 2016-08-19 | 83981位读者 | 引用在这篇文章中,我们暂停查词典方法的介绍,转而介绍字标注的方法。前面已经提到过,字标注是通过给句子中每个字打上标签的思路来进行分词,比如之前提到过的,通过4标签来进行标注(single,单字成词;begin,多字词的开头;middle,三字以上词语的中间部分;end,多字词的结尾。均只取第一个字母。),这样,“为人民服务”就可以标注为“sbebe”了。4标注不是唯一的标注方式,类似地还有6标注,理论上来说,标注越多会越精细,理论上来说效果也越好,但标注太多也可能存在样本不足的问题,一般常用的就是4标注和6标注。
值得一提的是,这种通过给每个字打标签、进而将问题转化为序列到序列的学习,不仅仅是一种分词方法,还是一种解决大量自然语言问题的思路,比如命名实体识别等任务,同样可以用标注的方法来做。回到分词来,通过字标注法来进行分词的模型有隐马尔科夫模型(HMM)、最大熵模型(ME)、条件随机场模型(CRF),它们在精度上都是递增的,据说目前公开评测中分词效果最好的是4标注的CRF。然而,在本文中,我们要讲解的是最不精确的HMM。因为在我看来,它并非一个特定的模型,而是解决一大类问题的通用思想,一种简化问题的学问。
这一切,还得从概率模型谈起。
基于双向LSTM和迁移学习的seq2seq核心实体识别
By 苏剑林 | 2016-09-06 | 160312位读者 | 引用暑假期间做了一下百度和西安交大联合举办的核心实体识别竞赛,最终的结果还不错,遂记录一下。模型的效果不是最好的,但是胜在“端到端”,迁移性强,估计对大家会有一定的参考价值。
比赛的主题是“核心实体识别”,其实有两个任务:核心识别 + 实体识别。这两个任务虽然有关联,但在传统自然语言处理程序中,一般是将它们分开处理的,而这次需要将两个任务联合在一起。如果只看“核心识别”,那就是传统的关键词抽取任务了,不同的是,传统的纯粹基于统计的思路(如TF-IDF抽取)是行不通的,因为单句中的核心实体可能就只出现一次,这时候统计估计是不可靠的,最好能够从语义的角度来理解。我一开始就是从“核心识别”入手,使用的方法类似QA系统:
1、将句子分词,然后用Word2Vec训练词向量;
2、用卷积神经网络(在这种抽取式问题上,CNN效果往往比RNN要好)卷积一下,得到一个与词向量维度一样的输出;
3、损失函数就是输出向量跟训练样本的核心词向量的cos值。
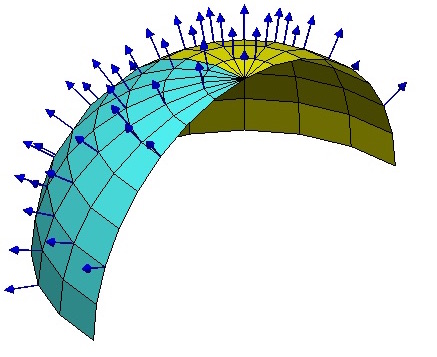
【理解黎曼几何】4. 联络和协变导数
By 苏剑林 | 2016-10-16 | 80308位读者 | 引用向量与联络
当我们在我们的位置建立起自己的坐标系后,我们就可以做很多测量,测量的结果可能是一个标量,比如温度、质量,这些量不管你用什么坐标系,它都是一样的。当然,有时候我们会测量向量,比如速度、加速度、力等,这些量都是客观实体,但因为测量结果是用坐标的分量表示的,所以如果换一个坐标,它的分量就完全不一样了。
假如所有的位置都使用同样的坐标,那自然就没有什么争议了,然而我们前面已经反复强调,不同位置的人可能出于各种原因,使用了不同的坐标系,因此,当我们写出一个向量$A^{\mu}$时,严格来讲应该还要注明是在$\boldsymbol{x}$位置测量的:$A^{\mu}(\boldsymbol{x})$,只有不引起歧义的情况下,我们才能省略它。
到这里,我们已经能够进行一些计算,比如$A^{\mu}$是在$\boldsymbol{x}$处测量的,而$\boldsymbol{x}$处的模长计算公式为$ds^2 = g_{\mu\nu} dx^{\mu} dx^{\nu}$,因此,$A^{\mu}$的模长为$\sqrt{g_{\mu\nu} A^{\mu}A^{\nu}}$,它是一个客观实体。
【中文分词系列】 5. 基于语言模型的无监督分词
By 苏剑林 | 2016-09-12 | 148420位读者 | 引用迄今为止,前四篇文章已经介绍了分词的若干思路,其中有基于最大概率的查词典方法、基于HMM或LSTM的字标注方法等。这些都是已有的研究方法了,笔者所做的就只是总结工作而已。查词典方法和字标注各有各的好处,我一直在想,能不能给出一种只需要大规模语料来训练的无监督分词模型呢?也就是说,怎么切分,应该是由语料来决定的,跟语言本身没关系。说白了,只要足够多语料,就可以告诉我们怎么分词。
看上去很完美,可是怎么做到呢?《2.基于切分的新词发现》中提供了一种思路,但是不够彻底。那里居于切分的新词发现方法确实可以看成一种无监督分词思路,它就是用一个简单的凝固度来判断某处该不该切分。但从分词的角度来看,这样的分词系统未免太过粗糙了。因此,我一直想着怎么提高这个精度,前期得到了一些有意义的结果,但都没有得到一个完整的理论。而最近正好把这个思路补全了。因为没有查找到类似的工作,所以这算是笔者在分词方面的一点原创工作了。
语言模型
首先简单谈一下语言模型。
【理解黎曼几何】1. 一条几何之路
By 苏剑林 | 2016-10-14 | 80832位读者 | 引用一个月没更新了,这个月花了不少时间在黎曼几何的理解方面,有一些体会,与大家分享。记得当初孟岩写的《理解矩阵》,和笔者所写的《新理解矩阵》,读者反响都挺不错的,这次沿用了这个名称,称之为《理解黎曼几何》。
黎曼几何是研究内蕴几何的几何分支。通俗来讲,就是我们可能生活在弯曲的空间中,比如一只生活在二维球面的蚂蚁,作为生活在弯曲空间中的个体,我们并没有足够多的智慧去把我们的弯曲嵌入到更高维的空间中去研究,就好比蚂蚁只懂得在球面上爬,不能从“三维空间的曲面”这一观点来认识球面,因为球面就是它们的世界。因此,我们就有了内蕴几何,它告诉我们,即便是身处弯曲空间中,我们依旧能够测量长度、面积、体积等,我们依旧能够算微分、积分,甚至我们能够发现我们的空间是弯曲的!也就是说,身处球面的蚂蚁,只要有足够的智慧,它们就能发现曲面是弯曲的——跟哥伦布环球航行那样——它们朝着一个方向走,最终却回到了起点,这就可以断定它们自身所处的空间必然是弯曲的——这个发现不需要用到三维空间的知识。
【理解黎曼几何】2. 从勾股定理到黎曼度量
By 苏剑林 | 2016-10-14 | 74243位读者 | 引用黎曼度量
几何,英文名是Geometry,原意是大地测量。既然是测量,就必须有参考物,还有得知道如何计算距离。
有了参照物,我们就可以建立坐标系,把每个点的坐标都写下来,至于计算距离,我们有伟大的勾股定理:
$$ds^2 = dx^2 + dy^2 \tag{1} $$
但这里我们忽略了两个问题。
第一个问题是,我们不一定使用直角坐标系,如果使用极坐标,那么应该是
$$ds^2 = dr^2 + r^2 d\theta^2 \tag{2} $$
因此可以联想,最一般的形式应该是
$$ds^2 = E(x^1, x^2)(dx^1)^2 + 2F(x^1, x^2)dx^1 dx^2 + G(x^1, x^2)(dx^2)^2 \tag{3} $$
这里的$x^1,x^2$是广义坐标,使用上标而不是下标来标记序号,是为了跟传统的教材记号一致。那这公式是什么意思呢?其实很简单,正如我们没理由要求全世界都使用人民币一样,我们没必要要求世界各地都使用同一个坐标系,而更合理的做法是,每一处地方都使用自己的坐标系(局部坐标系),然后给出当地计算距离的方法。因此,上述公式正是说,在位置$(x^1, x^2)$处计算向量$(dx^1, dx^2)$的长度的公式(当地的勾股定理)是$ds^2 = E(x^1, x^2)(dx^1)^2 + 2F(x_1, x_2)dx^1 dx^2 + G(x^1, x^2)(dx^2)^2$。









最近评论