《向量》系列——3.当天体力学遇到向量(1)

不知道各位读者还记得BoJone在《方程与宇宙》这一章中写了整整三篇文章来学习天体力学中的二体问题吗？虽然对二体问题基本上做了一个描述，但是依旧是冰山一角。而在最近写的几篇文章中，BoJone又强调了“向量”的巨大作用。那么，当天体力学与向量碰头后，会发生什么大事呢？难道，火星撞上了地球？

在《方程与宇宙》系列中，在开头我们便导出了二体问题的基本方程：
在二体问题中，选择其中一个质点为参照物，另一个质点的运动方程可以表示为：
$$\ddot{\vec{r}}=-\frac{\mu \vec{r}}{r^3}$$

$\mu=G(M+m)$。那么就从这个方程出发，运用向量以及一点点微积分知识，来完成天体力学中二体问题的解答。

首先我们来考虑$\vec{r}\times\dot{\vec{r}}=?$，首先求这个式子的导数
$$\frac{d}{dt}(\vec{r}\times\dot{\vec{r}})=\dot{\vec{r}}\times\dot{\vec{r}}+\vec{r}\times\ddot{\vec{r}}=0+\vec{r}\times(-\frac{\mu \vec{r}}{r^3})=0$$

只有常数的导数等于0，对于向量来说也只有常向量（方向和大小是常数）的导数才等于0，所以
$$\vec{r}\times\dot{\vec{r}}=\vec{k}\tag{1}$$
$\vec{k}$是常向量。这个其实就是角动量守恒的体现，$m\vec{r}\times\dot{\vec{r}}$就是质点相对于参照质点的角动量，由于力矩为0，所以角动量守恒。这个规律“翻译”成天体力学的语言，就是“开普勒第二定律”。

为了找出其他的常向量，我们来考虑下：$\vec{k}\times\ddot{\vec{r}}$，根据向量的知识，有
$$\vec{k}\times\ddot{\vec{r}}=(\vec{r}\times\dot{\vec{r}})\times(-\frac{\mu \vec{r}}{r^3})=-\frac{\mu}{r^3}[(\vec{r}\cdot \vec{r})\dot{\vec{r}}-(\vec{r}\cdot \dot{\vec{r}})\vec{r}]$$

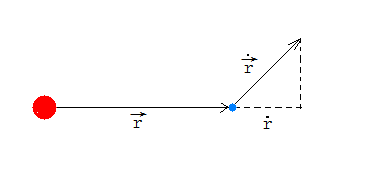
并且不难证明：$\vec{r}*\dot{\vec{r}}=r\dot{r}$（参考下图）

于是$\vec{k}\times\ddot{\vec{r}}=-\mu(\frac{\dot{\vec{r}}}{r}-\frac{r\vec{r}}{r^2})=\frac{d}{dt}(-\frac{\mu\vec{r}}{r})$

两边积分，就得到：$\vec{k}\times\dot{\vec{r}}=-\frac{\mu\vec{r}}{r}-\mu\vec{e}$。其中$-\mu\vec{e}$代表着一个常向量，我们把这条式子改写成：
$$\vec{k}\times\dot{\vec{r}}+\frac{\mu\vec{r}}{r}=-\mu\vec{e}\tag{2}$$
接下来求关于速度的积分（活力积分）
$$\frac{d}{dt}(1/2 \dot{\vec{r}^2})=\dot{\vec{r}}\cdot \ddot{\vec{r}}=\dot{\vec{r}}\cdot (-\frac{\mu \vec{r}}{r^3})=\frac{-\mu\dot{r}}{r^2}=\frac{d}{dt}(-\frac{\mu}{r})$$

两边积分：$1/2 \dot{\vec{r}}^2=-\frac{\mu}{r}+h$，或者写成$$1/2 v^2-\frac{\mu}{r}=h\tag{3}$$
接着，我们有$\vec{k}*\vec{e}=\vec{k}*(-\frac{\vec{k}\times\dot{\vec{r}}}{\mu}-\frac{\vec{r}}{r})=0$，这给出了
$$\mu^2(e^2-1)=2hk^2\tag{4}$$
其中$k=|\vec{k}|,e=|\vec{e}|$。至此，我们已经用向量方法求出了二体问题中关于能量和角动量的相关公式，并且为下一步的相关计算奠定了基础。接下来就是求出轨道方程、开普勒方程等解了。这利用向量知识可以一步到位。(待续....)

转载到请包括本文地址：https://spaces.ac.cn/archives/740

更详细的转载事宜请参考：《科学空间FAQ》