Dropout视角下的MLM和MAE：一些新的启发

大家都知道，BERT的MLM（Masked Language Model）任务在预训练和微调时的不一致，也就是预训练出现了[MASK]而下游任务微调时没有[MASK]，是经常被吐槽的问题，很多工作都认为这是影响BERT微调性能的重要原因，并针对性地提出了很多改进，如XL-NET、ELECTRA、MacBERT等。本文我们将从Dropout的角度来分析MLM的这种不一致性，并且提出一种简单的操作来修正这种不一致性。

同样的分析还可以用于何凯明最近提出的比较热门的MAE（Masked Autoencoder）模型，结果是MAE相比MLM确实具有更好的一致性，由此我们可以引出一种可以能加快训练速度的正则化手段。

Dropout #

首先，我们重温一下Dropout。从数学上来看，Dropout是通过伯努利分布来为模型引入随机噪声的操作，所以我们也简单复习一下伯努利分布。

伯努利分布 #

伯努利分布（Bernoulli Distribution）算得上是最简单的概率分布了，它是一个二元分布，取值空间是$\{0,1\}$，其中$\varepsilon$取1的概率为$p$，取0的概率为$1-p$，记为
\begin{equation}\varepsilon\sim \text{Bernoulli}(p)\end{equation}
伯努利分布的一个有趣的性质是它的任意阶矩都为$p$，即
\begin{equation}\mathbb{E}_{\varepsilon}[\varepsilon^n] = p\times 1^n + (1-p)\times 0^n = p\end{equation}
所以我们知道它的均值为$p$，以及方差为
\begin{equation}\mathbb{V}ar_{\varepsilon}[\varepsilon] = \mathbb{E}_{\varepsilon}[\varepsilon^2] - \mathbb{E}_{\varepsilon}[\varepsilon]^2 = p(1-p)\end{equation}

训练和预测 #

Dropout在训练阶段，将会以$1-p$将某些值置零，而其余值则除以$p$，所以Dropout事实上是引入了随机变量$\varepsilon\sim \text{Bernoulli}(p)$，使得模型从$f(x)$变成$f(x\varepsilon/p)$。其中$\varepsilon$可以有多个分量，对应多个独立的伯努利分布，但大多数情况下其结果跟$\varepsilon$是标量是没有本质区别，所以我们只需要针对$\varepsilon$是标量时进行推导。

在《又是Dropout两次！这次它做到了有监督任务的SOTA》中我们证明过，如果损失函数是MSE，那么训练完成后的最佳预测模型应该是
\begin{equation}\mathbb{E}_{\varepsilon}[f(x\varepsilon/p)]\end{equation}
这意味着我们应该要不关闭Dropout地预测多次，然后将预测结果进行平均来作为最终的预测结果，即进行“模型平均”。但很显然这样做计算量很大，所以实际中我们很少会用这种做法，更多的是直接关闭Dropout，即将$\varepsilon/p$改为1。而我们知道
\begin{equation}f(x)=f(x\,\mathbb{E}_{\varepsilon}[\varepsilon]/p)\end{equation}
所以关闭Dropout事实上是一种“权重平均”（将$\varepsilon$视为模型的随机权重）。也就是说，理论的最优解是“模型平均”，但由于计算量的原因，我们通常用“权重平均”来近似，它可以视为“模型平均”的一阶近似。

MLM模型 #

在这一节中，我们将MLM模型视为一种特殊的Dropout，由此可以清楚描述地预训练和微调的不一致之处，并且可以导出一个简单的修正策略，可以更好地缓解这种不一致性。

Dropout视角 #

简单起见，我们先来分析一个简化版本的MLM：假设在预训练阶段，每个token以$p$的概率保持不变，以$1-p$的概率被替换为[MASK]，并且第$i$个token的Embedding记为$x_i$，[MASK]的Embedding记为$m$，那么我们可以同样引入随机变量$\varepsilon\sim \text{Bernoulli}(p)$，将MLM的模型记为
\begin{equation}f(\cdots,x_i,\cdots)\quad\rightarrow\quad f(\cdots,x_i \varepsilon + m(1-\varepsilon),\cdots)\end{equation}
这样，MLM跟Dropout本质是相同的，它们都是通过伯努利分布给模型引入了随机扰动。现在，按照Dropout的常规用法，它的预测模型应该是“权重平均”，即
\begin{equation}f(\cdots,\mathbb{E}_{\varepsilon}[x_i \varepsilon + m(1-\varepsilon)],\cdots) = f(\cdots,x_i p + m (1-p),\cdots)\end{equation}
此时，MLM在微调阶段的不一致性就体现出来了：我们将预训练的MLM视为一种特殊的Dropout，那么微调阶段对应的是“取消Dropout”，按照常规做法，此时我们应该将每个token的Embedding改为$x_i p + m (1-p)$，但事实上我们没有，而是保留了原始的$x_i$。

修正Embedding #

按照BERT的默认设置，在训练MLM的时候，会有15%的token被选中来做MLM预测，而在这15%的token中，有80%的概率被替换为[MASK]，有10%的概率保持不变，剩下10%的概率则随机替换为一个随机token，这样根据上述分析，我们在MLM预训练完成之后，应该对Embedding进行如下调整：
\begin{equation}\text{Embedding[i]} \leftarrow 0.85\times \text{Embedding[i]} + 0.15\times\left(\begin{array}{l}0.8\times \text{Embedding[m]} \,+\\
0.1 \times \text{Embedding[i]} \,+ \\
0.1\times \text{Avg[Embedding]}\end{array}\right)
\end{equation}
其中$\text{Embedding[m]}$是[MASK]的Embedding，而$\text{Avg[Embedding]}$的全体token的平均Embedding。在bert4keras中，参考代码如下：

embeddings = model.get_weights()[0]  # 一般第一个权重就是Token Embedding
v1 = embeddings[tokenizer._token_mask_id][None]  # [MASK]的Embedding
v2 = embeddings.mean(0)[None]  # 平均Embedding
embeddings = 0.85 * embeddings + 0.15 * (0.8 * v1 + 0.1 * embeddings + 0.1 * v2)  # 加权平均
K.set_value(model.weights[0], embeddings)  # 重新赋值

那么，该修改是否跟我们期望的那样有所提升呢？笔者在CLUE上对比了BERT和RoBERTa修改前后的实验结果（baseline代码参考《bert4keras在手，baseline我有：CLUE基准代码》），结论是“没有显著变化”。

看到这里，读者也许会感到失望：敢情你前面说那么多都是白说了？笔者认为，上述操作确实是可以缓解预训练和微调的不一致性的（否则我们不是否定了Dropout？）；至于修改后的效果没有提升，意味着这种不一致性的问题并没有我们想象中那么严重，至少在CLUE的任务上是这样。一个类似的结果出现的MacBERT中，它在预训练阶段用近义词来代替[MASK]来修正这种不一致性，但笔者也在用同样的baseline代码测试过MacBERT，结果显示它跟RoBERTa也没显著差别。因此，也许只有在特定的任务或者更大的mask比例下，才能显示出修正这种不一致性的必要性。

MAE模型 #

不少读者可能已经听说过何凯明最近提出的MAE（Masked Autoencoder）模型，它以一种简单高效的方式将MLM任务引入到图像的预训练之中，并获得了有效的提升。在这一节中，我们将会看到，MAE同样可以作为一种特殊的Dropout来理解，从中我们可以得到一种防止过拟合的新方法。

Dropout视角 #

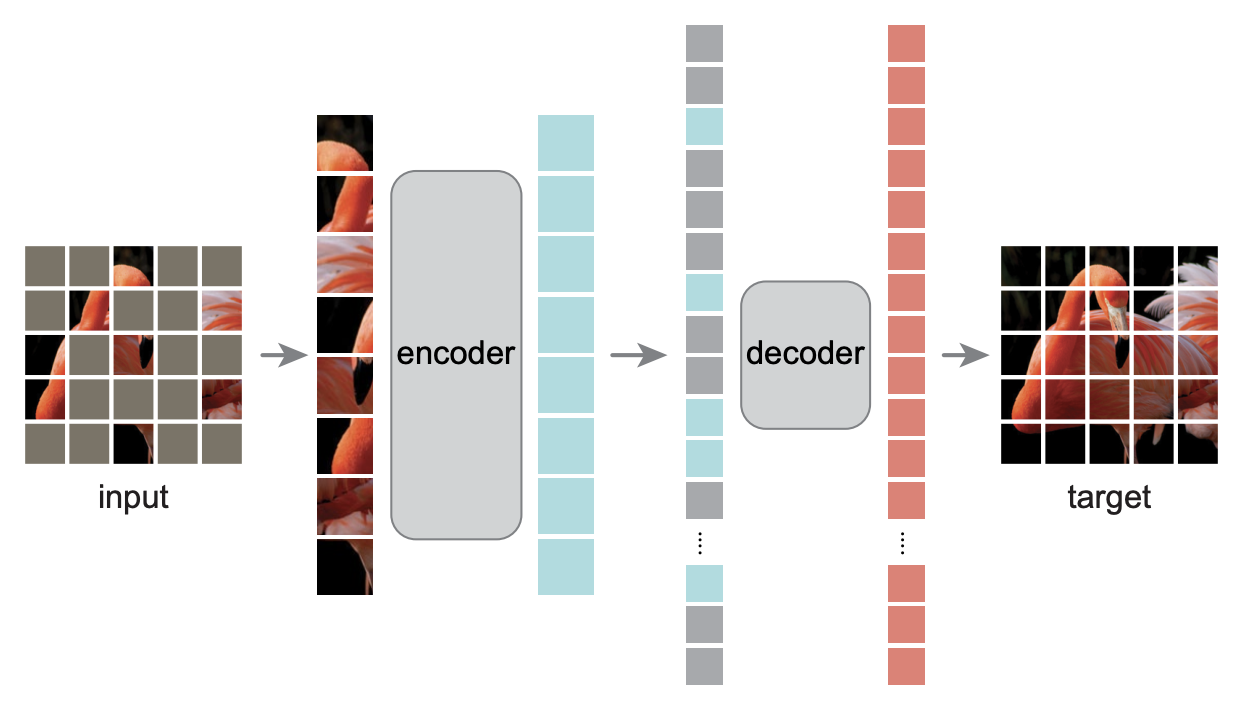
如下图所示，MAE将模型分为encoder和decoder两部分，并且具有“encoder深、decoder浅”的特点，然后它将[MASK]只放到decoder中，而encoder不处理[MASK]。这样一来，encoder要处理的序列就变短了，最关键的一步是，MAE使用了75%的mask比例，这意味着encoder的序列长度只有通常的1/4，加上“encoder深、decoder浅”的特点，总的来说模型的预训练速度快了3倍多！

MAE模型示意图

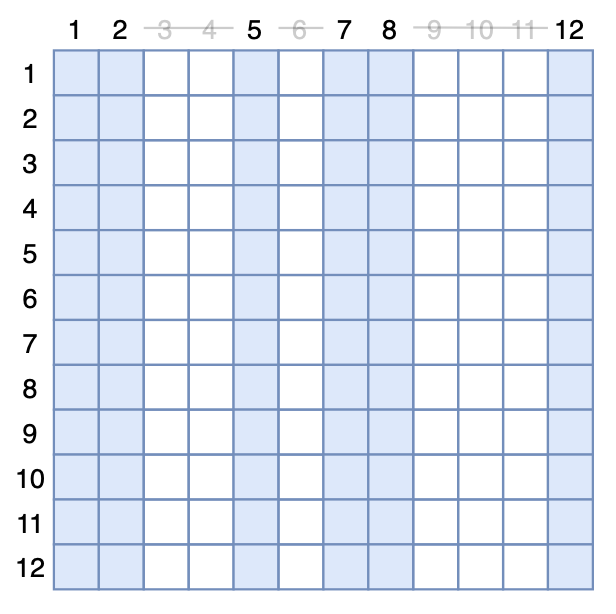
我们也可以从另一个角度来实现MAE模型：MAE把[MASK]从encoder中移除，这等价于剩下的token不与被mask掉的token交互，而对于Transformer模型来说，token之间的交互来源于Self Attention，所以我们依然可以保持原始输入，但在Attention矩阵中mask掉对应的列。如图所示，假设第$i$个token被mask掉，事实上就相当于Attention矩阵的第$i$列的所有元素被强制置0：

MAE的等价Attention Dropout示意图

当然，从实用的角度看，这种做法纯粹是浪费算力，但它有助于我们得到一个有意思的理论结果。我们设有$n$的输入token，原始的Attention矩阵为$A$（softmax后的），定义$M_i$为一个$n\times n$矩阵，它的第$i$列为0、其余都为1，然后定义随机矩阵$\tilde{M}_i$，它以$p$的概率为全1矩阵，以$1-p$的概率为$M_i$，那么MAE模型可以写成
\begin{equation}f(\cdots,A,\cdots)\quad\rightarrow\quad f(\cdots,\text{Norm}(A\otimes \tilde{M}_1\otimes \tilde{M}_2\otimes \cdots\otimes \tilde{M}_n),\cdots)\end{equation}
这里$\text{Norm}$是指将矩阵重新按行归一化；$\otimes$时逐个元素对应相乘；当有多个Attention层时，各个Attention层共用同一批$\tilde{M}_1,\tilde{M}_2,\cdots,\tilde{M}_n$。

这样，我们将MAE转换为了一种特殊的Attention Dropout。那么同样按照微调阶段“取消Dropout”的做法，我们知道它对应的模型应该是
\begin{equation}\begin{aligned}
&\,f(\cdots,\text{Norm}(A\otimes \mathbb{E}[\tilde{M}_1\otimes \tilde{M}_2\otimes \cdots\otimes \tilde{M}_n]),\cdots)\\
=&\,f(\cdots,\text{Norm}(A\otimes \mathbb{E}[\tilde{M}_1]\otimes \mathbb{E}[\tilde{M}_2]\otimes \cdots\otimes \mathbb{E}[\tilde{M}_n]),\cdots)\\
=&\,f(\cdots,\text{Norm}(Ap),\cdots)\\
=&\,f(\cdots,A,\cdots)
\end{aligned}\end{equation}
其中第二个等号是因为$\mathbb{E}[\tilde{M}_i]$是一个第$i$列为$p$、其余为1的矩阵，那么$\mathbb{E}[\tilde{M}_1]\otimes \mathbb{E}[\tilde{M}_2]\otimes \cdots\otimes \mathbb{E}[\tilde{M}_n]$事实上就是一个全为$p$的矩阵，所以与$A$相乘的结果等价于$A$直接乘以常数$p$；第三个等号则是因为全体元素乘以同一个常数，不影响归一化结果。

从这个结果中看到，对于MAE来说，“取消Dropout”之后跟原模型一致，这说明了MAE相比原始的MLM模型，不仅仅是速度上的提升，还具有更好的预训练与微调的一致性。

防止过拟合 #

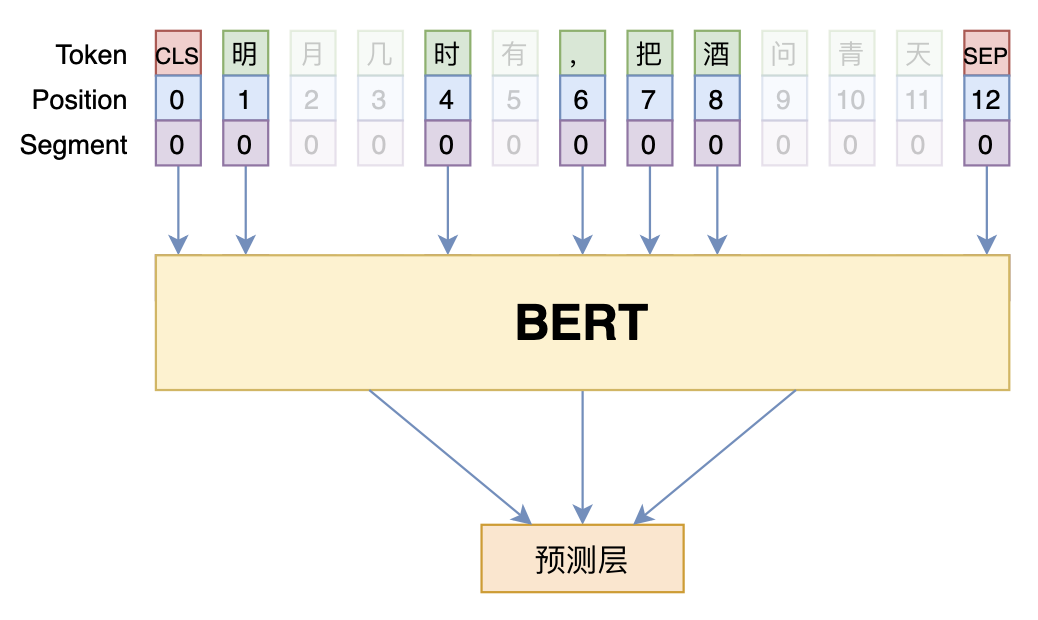
反过来想，既然MAE也可以视为一种Dropout，而Dropout有防止过拟合的作用，那么我们能不能将MAE的做法当作一种防止过拟合的正则化手段来使用呢？如下图所示，在训练阶段，我们可以随机扔掉一些token，但要保持剩余token的原始位置，我们暂且称之为“DropToken”：

DropToken示意图

之所以会这样想，是因为常规的Dropout虽然通常被直接地理解为采样一个子网络训练，但那纯粹是直观的想象，实际上Dropout的加入还会降低训练速度，而DropToken由于显式了缩短了序列长度，是可以提高训练速度的，如果有效那必然是一种非常实用的技巧。此外，有些读者可能已经试过删除某些字词的方式来进行数据扩增，它跟DropToken的区别在于DropToken虽然删除了一些Token，但依然保留了剩余token的原始位置，这个实现依赖于Transformer结构本身。

在CLUE上做的几个实验对比，基准模型为BERT base，下标的数字是drop比例，最终的效果参差不齐，除了IFLYTEK明确有效外，其他看缘分（其实很多防止过拟合手段都这样），最优drop比例在0.1～0.15之间：
$$\begin{array}{c}
\text{CLUE分类任务对比实验（验证集）} \\
{\begin{array}{c|ccccccc}
\hline
& \text{IFLYTEK} & \text{TNEWS} & \text{AFQMC} & \text{OCNLI} & \text{WSC} & \text{CSL} \\
\hline
\text{BERT}_{\text{0.00}} & 60.06 & 56.80 & 72.41 & 73.93 & 78.62 & 83.93 \\
\text{BERT}_{\text{0.10}} & 60.56 & 57.00 & 72.61 & 73.76 & 77.30 & 83.33\\
\text{BERT}_{\text{0.15}} & 60.10 & 56.68 & 72.50 & 74.54 & 77.30 & 83.30\\
\text{BERT}_{\text{0.25}} & 61.29 & 56.88 & 72.34 & 73.09 & 73.68 & 83.37\\
\text{BERT}_{\text{0.50}} & 61.45 & 57.02 & 69.76 & 70.68 & 69.41 & 82.56\\
\hline
\end{array}}
\end{array}$$

本文小结 #

本文从Dropout的视角考察了MLM和MAE两个模型，它们均可视为特殊的Dropout，从这个视角中，我们可以得到了一种修正MLM的不一致性的技巧，以及得到一种类似MAE的防止过拟合技巧。

转载到请包括本文地址：https://spaces.ac.cn/archives/8770

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。