Transformer升级之路:8、长度外推性与位置鲁棒性
By 苏剑林 | 2023-01-31 | 77795位读者 |上一篇文章《Transformer升级之路:7、长度外推性与局部注意力》我们讨论了Transformer的长度外推性,得出的结论是长度外推性是一个训练和预测的不一致问题,而解决这个不一致的主要思路是将注意力局部化,很多外推性好的改进某种意义上都是局部注意力的变体。诚然,目前语言模型的诸多指标看来局部注意力的思路确实能解决长度外推问题,但这种“强行截断”的做法也许会不符合某些读者的审美,因为人工雕琢痕迹太强,缺乏了自然感,同时也让人质疑它们在非语言模型任务上的有效性。
本文我们从模型对位置编码的鲁棒性角度来重新审视长度外推性这个问题,此思路可以在基本不对注意力进行修改的前提下改进Transformer的长度外推效果,并且还适用多种位置编码,总体来说方法更为优雅自然,而且还适用于非语言模型任务。
问题分析 #
在之前的文章中,我们分析了长度外推性的缘由,给出了“长度外推性是一个训练和预测的长度不一致的问题”的定位,具体不一致的地方则有两点:
1、预测的时候用到了没训练过的位置编码(不管绝对还是相对);
2、预测的时候注意力机制所处理的token数量远超训练时的数量。
其中,第2点说的是更多的token会导致注意力更加分散(或者说注意力的熵变大),从而导致的训练和预测不一致问题,其实我们在《从熵不变性看Attention的Scale操作》已经初步讨论并解决了它,答案是将Attention从
\begin{equation}Attention(Q,K,V) = softmax\left(\frac{QK^{\top}}{\sqrt{d}}\right)V\end{equation}
修改为
\begin{equation}Attention(Q,K,V) = softmax\left(\frac{\log_{m} n}{\sqrt{d}}QK^{\top}\right)V\end{equation}
其中$m$是训练长度,$n$是预测长度。经过这样修改(下面简称为“$\log n$缩放注意力”),注意力的熵随着长度的变化更加平稳,缓解了这个不一致问题。个人的实验结果显示,至少在MLM任务上,“$\log n$缩放注意力”的长度外推表现更好。
所以,我们可以认为第2点不一致性已经得到初步解决,那么接下来应该是先集中精力解决第1点不一致性。
随机位置 #
第1点不一致性,即“预测的时候用到了没训练过的位置编码”,那么为了解决它,就应该做到“训练阶段把预测所用的位置编码也训练一下”。一篇ACL22还在匿名评审的论文《Randomized Positional Encodings Boost Length Generalization of Transformers》首次从这个角度考虑了该问题,并且提出了解决方案。
论文的思路很简单:
随机位置训练 设$N$为训练长度(论文$N=40$),$M$为预测长度(论文$M=500$),那么选定一个较大$L > M$(这是一个超参,论文$L=2048$),训练阶段原本长度为$N$的序列对应的位置序列是$[0,1,\cdots,N-2,N-1]$,现在改为从$\{0,1,\cdots,L-2,L-1\}$中随机不重复地选$N$个并从小到大排列,作为当前序列的位置序列。
基于numpy的参考代码为:
def random_position_ids(N, L=2048):
"""从[0, L)中随机不重复挑N个整数,并从小到大排列
"""
return np.sort(np.random.permutation(L)[:N])
预测阶段,也可以同样的方式随机采样位置序列,也可以直接在区间中均匀取点(个人的实验效果显示均匀取点的效果一般好些),这就解决了预测阶段的位置编码没有被训练过的问题。不难理解,这是一个很朴素的训练技巧(下面称之为“随机位置训练”),目标是希望Transformer能对位置的选择更加鲁棒一些,但后面我们将看到,它能取得长度外推效果的明显提升。笔者也在MLM任务上做了实验,结果显示在MLM上也是有效果的,并且配合“$\log n$缩放注意力”提升幅度更明显(原论文没有“$\log n$缩放注意力”这一步)。
新的基准 #
很多相关工作,包括上一篇文章提到的各种Local Attention及其变体的方案,都以语言模型任务构建评测指标,但不管是单向GPT还是双向的MLM,它们都高度依赖局部信息(局域性),所以之前的方案很可能只是因为语言模型的局域性才有良好的外推表现,假如换一个非局域性的任务,效果可能就变差了。也许正因为如此,这篇论文的评测并非是常规的语言模型任务,而是Google去年在论文《Neural Networks and the Chomsky Hierarchy》专门提出的一个长度外泛化基准(下面简称该测试基准为“CHE基准”,即“Chomsky Hierarchy Evaluation Benchmark”),这给我们提供了理解长度外推的一个新视角。
这个基准包含多个任务,分为R(Regular)、DCF(Deterministic Context-Free)、CS(Context-Sensitive)三个级别,每个级别的难度依次递增,每个任务的简介如下:
Even Pairs,难度R,给定二元序列,如“aabba”,判断2-gram中ab和ba的总数是否为偶数,该例子中2-gram有aa、ab、bb、ba,其中ab和ba共有2个,即输出“是”,该题也等价于判断二元序列的首尾字符是否相同。
Modular Arithmetic (Simple),难度R,计算由$\{0, 1, 2, 3, 4\}$五个数和$\{+,-,\times\}$三个运算符组成的算式的数值,并输出模5后的结果,比如输入$1 + 2 − 4$,那么等于$-1$,模5后等于$4$,所以输出$4$。
Parity Check,难度R,给定二元序列,如“aaabba”,判断b的数目是否为偶数,该例子中b的数目为2,那么输出“是”。
Cycle Navigation,难度R,给定三元序列,其中每个元分别代表$+0$、$+1$、$-1$之一,输出从0出发该序列最终的运算结果模5的值,比如$0,1,2$分别代表$+0,+1,-1$,那么$010211$代表$0 + 0 + 1 + 0 − 1 + 1 + 1 = 2$,模5后输出$2$。
Modular Arithmetic,难度DCF,计算由$\{0, 1, 2, 3, 4\}$五个数、括号$(,)$和$\{+,-,\times\}$三个运算符组成的算式的数值,并输出模5后的结果,比如输入$−(1−2)\times(4−3\times(−2))$,那么结果为$10$,模5后等于$0$,所以输出$0$,相比Simple版本,该任务多了“括号”,使得运算上更为复杂。
Reverse String,难度DCF,给定二元序列,如“aabba”,输出其反转序列,该例子中应该输出“abbaa”。
Solve Equation,难度DCF,给定由$\{0, 1, 2, 3, 4\}$五个数、括号$(,)$、$\{+,-,\times\}$三个运算符和未知数$z$组成的方程,求解未知数$z$的数值,使得它在模5之下成立。比如$−(1−2)\times(4−z\times(−2))=0$,那么$z=3$,解方程虽然看上去更难,但由于方程的构造是在Modular Arithmetic的基础上将等式中的某个数替换为$z$,所以保证有解并且解在$\{0, 1, 2, 3, 4\}$,因此理论上我们可以通过枚举结合Modular Arithmetic来求解,因此它的难度跟Modular Arithmetic相当。
Stack Manipulation,难度DCF,给定二元序列,如“abbaa”,以及由“POP/PUSH a/PUSH b”三个动作组成的堆栈操作序列,如“POP / PUSH a / POP”,输出最后的堆栈结果,该例子中应该输出“abba”。
Binary Addition,难度CS,给定两个二进制数,输出它们的和的二进制表示,如输入$10010$和$101$,输出$10111$,注意,这需要都在字符层面而不是数值层面输入到模型中进行训练和预测,并且两个数字是串行而不是并行对齐地提供的(可以理解为输入的是字符串$10010+101$)。
Binary Multiplication,难度CS,给定两个二进制数,输出它们的积的二进制表示,如输入$100$和$10110$,输出$1011000$,同Binary Addition一样,这需要都在字符层面而不是数值层面输入到模型中进行训练和预测,并且两个数字是串行而不是并行对齐地提供的(可以理解为输入的是字符串$100\times 10110$)。
Compute Sqrt,难度CS,给定一个二进制数,输出它的平方根的下取整的二进制表示,如输入$101001$,那么输出结果为$\lfloor\sqrt{101001}\rfloor=101$,这个难度同Binary Multiplication,因为至少我们可以从$0$到所给数结合Binary Multiplication逐一枚举来确定结果。
Duplicate String,难度CS,给定一个二元序列,如“abaab”,输出重复一次后的序列,该例子应该输出“abaababaab”,这个简单的任务看上去是难度R,但实际上是CS,大家可以想想为什么。
Missing Duplicate,难度CS,给定一个带有缺失值的二元序列,如“ab_aba”,并且已知原始的完整序列是一个重复序列(上一个任务的Duplicate String),预测确实值,该例子应该输出a。
Odds First,难度CS,给定一个二元序列$t_1 t_2 t_3 \cdots t_n$,输出$t_1 t_3 t_5 \cdots t_2 t_4 t_6 \cdots$,如输入aaabaa,将输出aaaaba。
Bucket Sort,难度CS,给定一个$n$元数值序列(数列中的每个数都是给定的$n$个数之一),返回其从小到大排序后的序列,如输入$421302214$应该输出$011222344$。
可以看到,这些任务都具有一个共同特点,就是它们的运算都有固定的简单规则,并且理论上输入都是不限长度的,那么我们可以通过短序列来训练,然后测试在短序列上的训练结果能否推广到长序列中。也就是说,它可以作为长度外推性的一个很强的测试基准。
实验结果 #
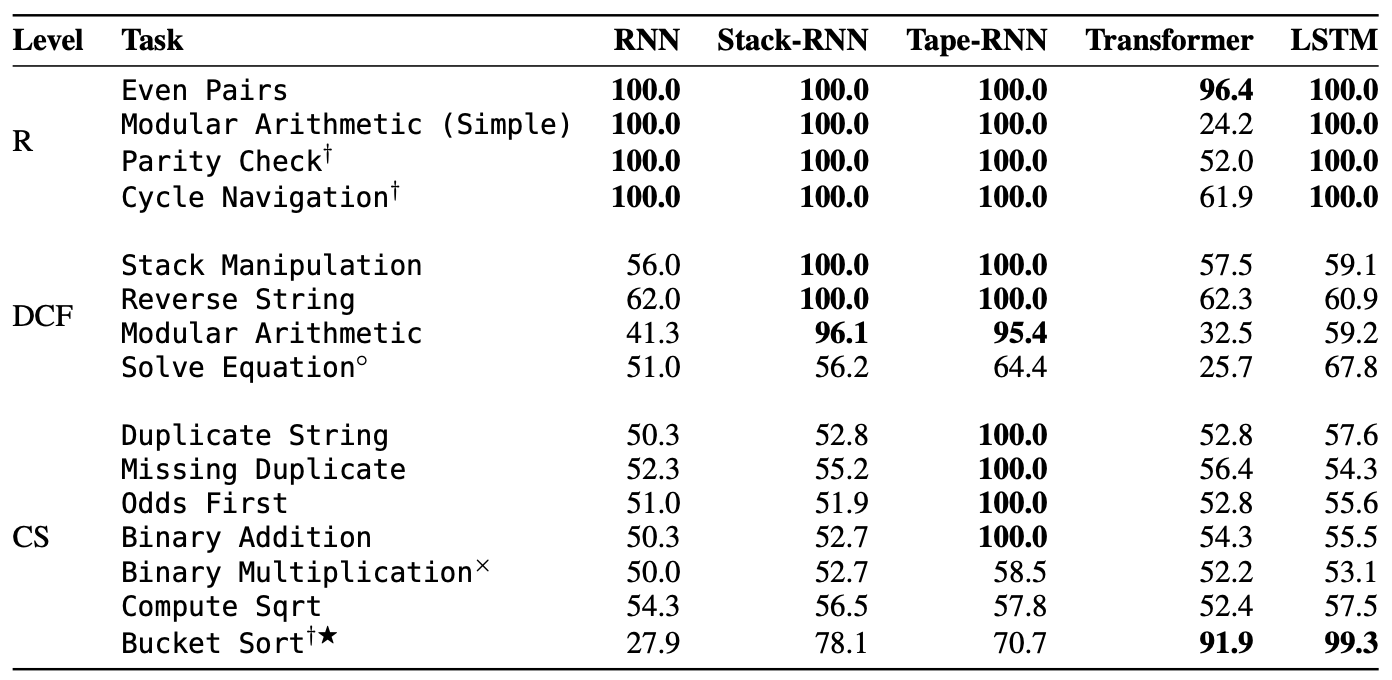
首先,介绍原始论文《Neural Networks and the Chomsky Hierarchy》的实验结果,它对比了若干RNN模型及Transformer模型的效果(评测指标是诸位字符串的平均准确率,而不是整体结果的全对率):
结果可能会让人意外,“风头正盛”的Transformer的长度外推效果是最差的(这里的Transformer还测试了不同的位置编码,并在每种任务上取了最优值),最好的是Tape-RNN。论文给它们的评级如下:
$$\underbrace{\text{Transformer}}_{\text{R}^-} < \underbrace{\text{RNN}}_{\text{R}} < \underbrace{\text{LSTM}}_{\text{R}^+} < \underbrace{\text{Stack-RNN}}_{\text{DCF}} < \underbrace{\text{Tape-RNN}}_{\text{CS}}$$
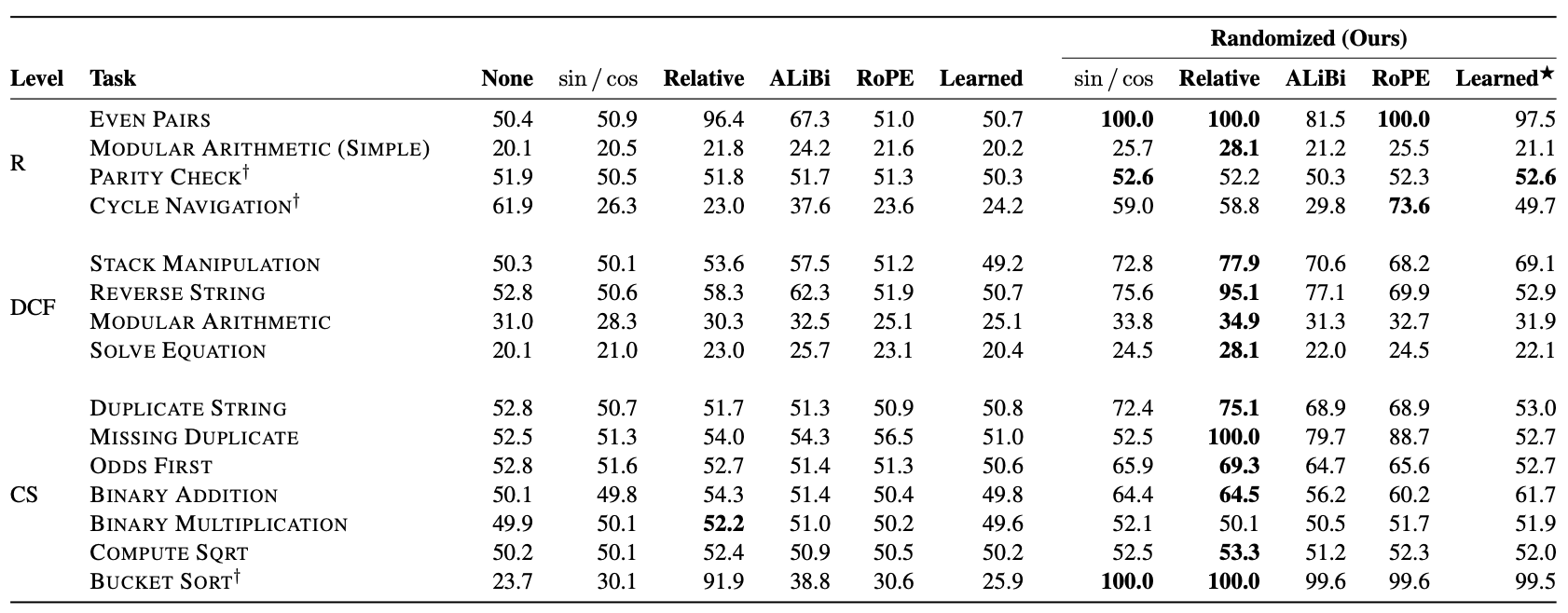
而前面介绍的《Randomized Positional Encodings Boost Length Generalization of Transformers》所提的随机位置训练方法,则为Transformer挽回了一些劣势:
可以看到,在随机位置训练之下,不管哪种位置编码的Transformer都有明显的提升,这就进一步验证了上一篇文章的结论,即长度外推性跟位置编码本身的设计没太大关系。特别地,随机位置训练还在Bucket Sort这个任务上首次取得了全对的准确率。尽管在总体表现上依然欠佳,但这相比之前的结果已经算是长足进步了(不知道结合“$\log n$缩放注意力”能否有提升?)。值得注意的地方还有,上表显示ALIBI这个在语言模型任务中表现良好的方法,在CHE基准上并无表现出什么优势,尤其是加入随机位置训练后,它的平均指标比RoPE还差,这就初步肯定了前面的猜测,即各种Local Attention变体的方法表现良好,大概率是因为基于语言模型的评测任务本身有严重的局域性,对于非局域性的CHE基准,这些方法并没有优势。
原理反思 #
细思之下,“随机位置训练”会很让人困惑。简单起见,我们不妨设$L=2048,N=64,M=512$,这样一来,训练阶段所用的平均位置序列大致为$[0, 32, 64, \cdots, 2016]$,预测阶段所用的平均位置序列是$[0, 4, 8, \cdots, 2044]$,训练阶段和预测阶段的相邻位置差不一样,这也可以说是某种不一致性,但它表现依然良好,这是为什么呢?
我们可以从“序”的角度去理解它。由于训练阶段的位置id是随机采样的,那么相邻位置差也是随机的,所以不管是相对位置还是绝对位置,模型不大可能通过精确的位置id来获取位置信息,取而代之是一个模糊的位置信号,更准确地说,是通过位置序列的“序”来编码位置而不是通过位置id本身来编码位置。比如,位置序列[1,3,5]跟[2,4,8]是等价的,因为它们都是从小到大排列的一个序列,随机位置训练“迫使”模型学会了一个等价类,即所有从小到大排列的位置序列都是等价的,都可以相互替换,这是位置鲁棒性的真正含义。
然而,笔者自己在MLM上做的实验结果显示,这个“等价类”的学习对模型还是有一定的困难的,更理想的方法是训练阶段依然使用随机位置,使得预测阶段的位置编码也被训练过,但是预测阶段的位置序列前面部分应该跟随机位置的平均结果一致。还是刚才的例子,如果预测阶段所用的位置序列是$[0, 4, 8, \cdots, 2044]$,那么我们希望训练阶段的随机位置平均结果是$[0, 4, 8, \cdots, 252]$(即序列$[0, 4, 8, \cdots, 2044]$的前$N$个),而不是$[0, 32, 64, \cdots, 2016]$,这样训练和预测的一致性就更加紧凑了。
延伸推广 #
于是,笔者考虑了如下思路:
等均值随机位置训练 设$n$服从一个均值为$N$、采样空间为$[0, \infty)$的分布,那么训练阶段随机采样一个$n$,然后从$[0, n]$中均匀取$N$个点作为位置序列。
参考代码为:
def random_position_ids(N):
"""先随机采样n,然后从[0, n]均匀取N个点
"""
n = sample_from_xxx()
return np.linspace(0, 1, N) * n
注意,这样采样出来的位置序列是浮点数,因此不适用于离散的训练式位置编码,只适用于函数式位置编码如Sinusoidal或RoPE,下面假设只考虑函数式位置编码。
该思路的最大问题是如何选择适合的采样分布。笔者的第一反应是泊松分布,但考虑到泊松分布的均值和方差都是$n$,那么按照“3$\sigma$法则”来估算,它只能外推到$n+3\sqrt{n}$长度,这显然太短了。经过挑选和测试,笔者发现有两个分布比较适合:一个是指数分布,它的均值和标准差都是$n$,那么即便按照“3$\sigma$法则”,也能外推到$4n$的长度,是一个比较理想的范围(实际还更长些);另一个是beta分布,它定义在$[0,1]$上,我们可以将测试长度作为1,那么训练长度就是$N/M\in(0,1)$,beta分布有两个参数$\alpha,\beta$,其中均值为$\frac{\alpha}{\alpha+\beta}$,那么确保均值等于$N/M$后,我们还有额外的自由度控制$1$附近的概率,适合想要进一步拓展外推范围的场景。
笔者的实验结果显示,“等均值随机位置训练”结合“$\log n$缩放注意力”,在MLM任务上,能取得最佳的外推效果(训练长度64,测试长度512,采样分布为指数分布)。因为之前没做过CHE基准,所以笔者一时之间也没法测试CHE基准的效果,只能留到后面有机会再尝试了。
文章小结 #
本文从位置鲁棒性的角度思考了Transformer的长度外推性,得到了“随机位置训练”等增强长度外推性的新方案。同时,我们介绍了新的“CHE基准”,相比常规的语言模型任务,它具备更强的非局域性,可以更有效地评估长度外推相关工作。在它之下,之前的注意力局部化相关方法并没有较为突出的表现,相比之下“随机位置训练”效果更佳,这提醒我们应当在更全面的任务上评估相关方法的有效性,而不单单局限于语言模型任务。
转载到请包括本文地址:https://spaces.ac.cn/archives/9444
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 31, 2023). 《Transformer升级之路:8、长度外推性与位置鲁棒性 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/9444
@online{kexuefm-9444,
title={Transformer升级之路:8、长度外推性与位置鲁棒性},
author={苏剑林},
year={2023},
month={Jan},
url={\url{https://spaces.ac.cn/archives/9444}},
}










January 31st, 2023
这里的che基准就是测试模型是否具有解析正则语言、上下文无关语言、以及上下文有关语言语义的能力吧,也就是看神经模型能不能模拟有限状态机、下推自动机以及线性有界自动机。对这三种语言的解析transformer相比rnn是有天然劣势的,其原因就是注意力机制的无序性以及作为补偿的位置编码的次优性,用这三种语言比较rnn和transformer的话后者确实吃亏的。自然语言跟这三种语言明显不一样,众多实践已经证明transformer的自然语言语义解析能力远大于rnn的。这就带来一个问题:用che基准衡量transformer长度外推能力所得到的优劣结论,可以作为其对自然语言长度外推能力的有效参考吗?
用 CHE 测试 transformer 的确意义不大,transformer 的架构决定了它不可能精确建模 parity,长度外推更是无从谈起,见这篇文章 https://arxiv.org/abs/1906.06755 。背后的原因是 transformer 类似于 constant depth circuit,具有 O(n) 大小的内存但是只能进行 O(1) 深度的计算,因此建模不了正则语言。相反 RNN 类似于有限状态机,能进行 O(n) 深度的计算但是只有 O(1) 大小的内存,因此无法进行 symbol lookup,例如 {'abc': 1, 'bba': 2, 'ba': 3}['abc'] = 。显然,symbol lookup 才是对自然语言更有用的能力,而如果要用它来衡量外推能力,那么限制因素并不是位置编码,而是 key space dimension。所以,我的猜想是,自然语言外推能力不取决于位置编码,而取决于 key space dimension(当然,首先要使用 log(n) scaling)。
受教了,获益良多。事实上,“$\log n$缩放“更早地出现在 https://arxiv.org/abs/2202.12172 论文中,确实是作为改善PARITY和FIRST任务效果来提出的。另外,有没有可能key_size也随之动态变化,这确实是一个很值得思考的问题~
一个小问题请教一下!这里讨论的key space dimension是指的模型token dictionary的大小,还是attention head里的KVQ embedding vector的大小,还是别的呀?谢谢!
应该是你说的后者
我的观点是这样的:
1、CHE基准更多的是一种“完备性”测试,Transformer理论上也是一个万能拟合器,那么原则上它也能做这些任务,研究怎么把它做出来也是一件有意思的事情;
2、即便限制在自然语言中,现实世界的对话也可能出现CHE的某些任务或其变体,比如“Even Pairs”等价于判断首尾字符是否相同,而对话中我们一开始可能先讨论过某个话题,然后在对话结束时反问我们一开始是否讨论过该话题;
3、即便限制在“自然语言+单向语言模型”(GPT)中,目前的评测依然过度关注局部准确率(语言模型本身的特性确定),所以local attention相关方法表现良好,实际上这长度外推评测中,我们是否应该更关心那些远距离token的ppl?比如“xxxx A xxxxx A”,在“xxxx”和“xxxxx”(较长距离的上下文)都没出现过A,那么计算“xxxx A xxxxx _”出现A的概率,如果是这种评测,local attention效果还好不?
4、我个人对“随机位置训练”的实验,是在自然语言的MLM任务上进行的,结果表明也有提升,这说明对CHE有效的方法,对自然语言很可能也有效,而论文关于ALIBI的实验结果则表明反之不一定成立;
5、也许CHE对自然语言参考价值真的不大,但语言模型的外推评测对自然语言参考价值也未必大(除非我们真的打算所有自然语言任务都用GPT来做),我想象中,至少要有一个类似superglue的包含多种任务的榜单,其中训练集和预训练数据集都是短文本的,然后测试集是长文本的,这样才能真正的评价出Transformer及各种方法在自然语言任务下的长度外推能力。
1. 从 RNN 到 NTM 再到 transformer,我们得到的一个重要教训是不应该在单个神经网络里追求完备性。完备性应该由某种 "outer loop" 实现,例如 in-context retrieval 和 CoT,而单个神经网络只需要完成人类直觉可以完成的任务即可。另外,万能拟合器只有在不外推的前提下才成立。
2. even pairs 的实验可能做的有问题,我自己实验 40 长度训练可以 100% 准确率外推到 10000 长度。
3. “xxxx A xxxxx A” 的确不能用 local attention 完成,不过我想表达的是我们不需要 global PE,例如上面 even pairs 我用的就是 global attention + local PE。另外如第 1 点所述,即使单靠 transformer 完成不了也没关系,毕竟人类也不能光靠脑子记得很久之前的东西,也需要翻书。
1、之所以后面的LLM都用Attention而不是RNN,我理解主要是因为速度,而非RNN的完备性妨碍了它更好地理解语言,或者说Attention突出了自然语言更需要的特性,但没有证据显示完备性的进一步加入(在同一个网络中)会带来负面作用;
2、你是不是在首尾加入了[CLS]和[SEP]之类的标记?否则我很难理解local PE怎么起到这个作用(哭笑),不过,原论文的even pairs在relative位置编码上,确实也做到了九十多的准确率了,relative位置编码也是local PE的;
3、其实这归根结底是一个审美问题了,单单将“语言模型的长度外推”作为一个工程任务或者比赛任务的话,想必会有各种百花齐放的做法出现,比如直接截断上下文序列(而不是Attention矩阵)就是一个很强的baseline,甚至应该比local attention还好,对于我个人来说,只是想看看单个模型的极限和瓶颈。
February 1st, 2023
原理反思一节的预测平均位置是否写错了,[0,8,...2040] 只有256个位置,而不是512
对对,写作的时候想反了,已经修正,谢谢,为仔细阅读点赞!
February 10th, 2023
苏神能否将longformer(或其他局部attention模型)及其中文预训练版引入到bert4keras吗 keras和pytorch两个生态横跳太累了
这个短期内应该没有计划,抱歉~最近也没有什么开发的劲头(捂脸)
February 11th, 2023
看过了苏神上一篇文章后就很直观地想到了这个解决方案:对训练序列中的token赋予跳跃式的位置编码,从而保证模型“见过”更大跨度的位置差。翻到下一篇发现正好是讨论这个问题,可以不用自己去实验一下了。
文中提到这篇$\href{https://openreview.net/forum?id=nMYj4argap}{\text{《Randomized Positional Encodings Boost Length Generalization of Transformers》}}$和等均值随机位置训练,从我的直观感受上是一致的,就是让模型在训练中可以接触到不同跨度位置编码的训练。原始的$\text{linspace}(0,1,N)$提供局部注意力的训练,而跨越式的$\text{linspace}(0,n,n*N)$提供后续的外推能力。
那么从理想角度来说,是否应当希望不同步长的位置编码序列分布,应该和外推数据在预测时不同长度注意力的分布一致。也就是说应当先采样一部分目标数据进行分析,并且对应地设计训练时候使用的位置编码的分布。从这个角度讲,beta分布这种可以自由调整测试长度附近采样概率的分布可能会更适合需要全局建模的任务。
之所以出现“train short, test long”,可能有两个原因:一是训练的时候确实只能拿到short的样本,测试的时候则要处理long的;二是想要降低训练成本,所以训练的时候把原本long的样本截断为short。
对于第一个可能,我们训练阶段所统计出来的样本长度分布,无法代表测试情况;对于第二个可能,我们即便能够知道测试情况的样本长度分布,但我们没有足够算力按照测试阶段的分布进行处理。所以要在训练时模拟测试长度分布,似乎是很难的事情。
我这里仅仅是想让训练阶段的short能够随机地跳到long的位置编码,但是均值依然保持为short,并没有想着模拟样本本身的长度分布。
November 8th, 2023
"一篇ACL22还在匿名评审的论文《Randomized Positional Encodings Boost Length Generalization of Transformers》首次从这个角度考虑了该问题"
实际上第一次验证这一方法有效性的工作是 David Chiang 组里的工作《Data Augmentation by Concatenation for Low-Resource Translation: A Mystery and a Solution》Section 3.2,发表在IWSLT 2021。
感谢告知。
1、就这篇论文的标题而言,怕是我怎么搜相关文献都搜不出这篇论文...
2、看了看,Section 3.2是Position shifting,操作上确实有点相通之处,但不完全一样,它这个更像是最近出的PoSE:https://arxiv.org/abs/2309.10400
哈哈哈,是的是的,这个文章还是比较偏门的,不过确实是我看到的最早验证“训练时引入PE的随机性有利于提高模型推理的泛化性”的工作。
March 8th, 2024
"""还是刚才的例子,如果预测阶段所用的位置序列是[0,4,8,⋯,2044],那么我们希望训练阶段的随机位置平均结果是[0,4,8,⋯,252](即序列[0,4,8,⋯,2044]的前N个),而不是[0,32,64,⋯,2016],这样训练和预测的一致性就更加紧凑了。"""
这样的话预测时候的位置编码在训练的时候还是没见过?
训练见过呀,训练的时候位置编码是随机的,只不过平均结果是这个。
April 6th, 2025
[...]Transformer升级之路:8、长度外推性与位置鲁棒性[...]
July 22nd, 2025
“Binary Multiplication,难度CS,给定两个二进制数,输出它们的 和 的二进制表示”,是不是应该是输出他们 乘积 的二进制表示
感谢,已经修正。