用时间换取效果:Keras梯度累积优化器
By 苏剑林 | 2019-07-08 | 88731位读者 | 引用现在Keras中你也可以用小的batch size实现大batch size的效果了——只要你愿意花n倍的时间,可以达到n倍batch size的效果,而不需要增加显存。
Github地址:https://github.com/bojone/accum_optimizer_for_keras
扯淡
在一两年之前,做NLP任务都不用怎么担心OOM问题,因为相比CV领域的模型,其实大多数NLP模型都是很浅的,极少会显存不足。幸运或者不幸的是,Bert出世了,然后火了。Bert及其后来者们(GPT-2、XLNET等)都是以足够庞大的Transformer模型为基础,通过足够多的语料预训练模型,然后通过fine tune的方式来完成特定的NLP任务。
也来谈谈RNN的梯度消失/爆炸问题
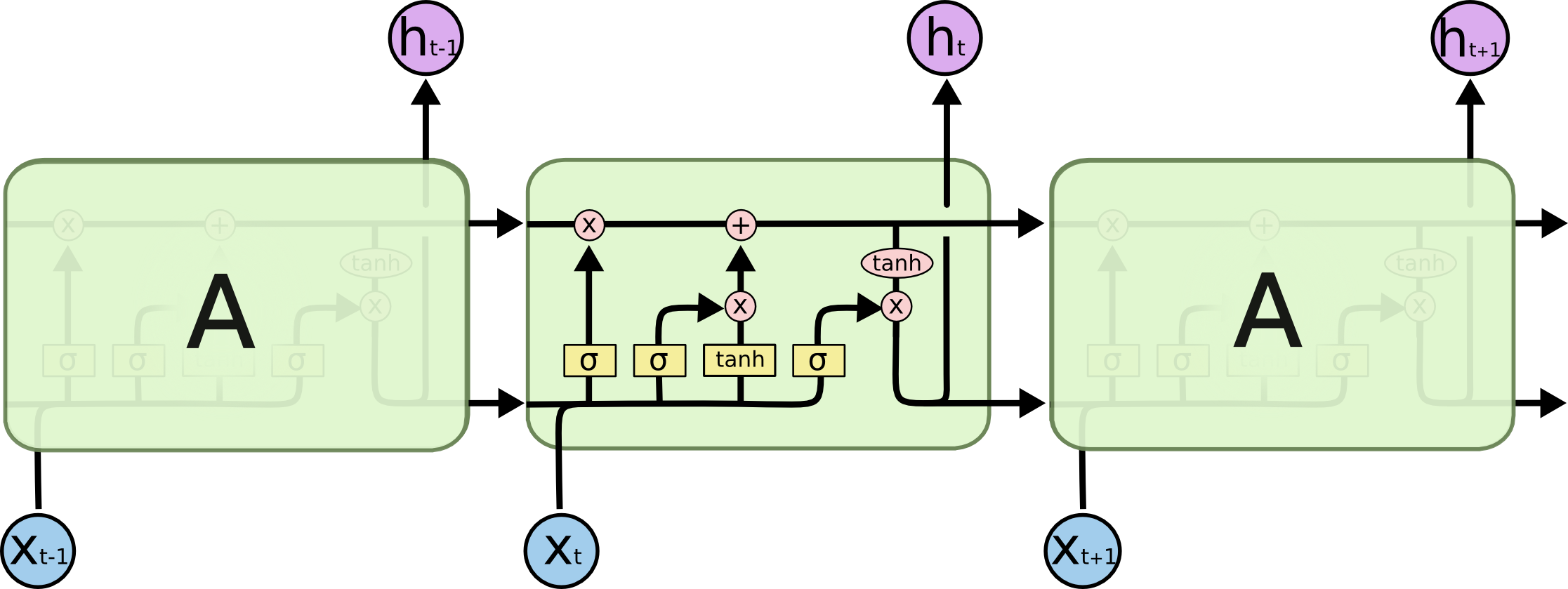
By 苏剑林 | 2020-11-13 | 103520位读者 | 引用尽管Transformer类的模型已经攻占了NLP的多数领域,但诸如LSTM、GRU之类的RNN模型依然在某些场景下有它的独特价值,所以RNN依然是值得我们好好学习的模型。而对于RNN梯度的相关分析,则是一个从优化角度思考分析模型的优秀例子,值得大家仔细琢磨理解。君不见,诸如“LSTM为什么能解决梯度消失/爆炸”等问题依然是目前流行的面试题之一...
关于此类问题,已有不少网友做出过回答,然而笔者查找了一些文章(包括知乎上的部分回答、专栏以及经典的英文博客),发现没有找到比较好的答案:有些推导记号本身就混乱不堪,有些论述过程没有突出重点,整体而言感觉不够清晰自洽。为此,笔者也尝试给出自己的理解,供大家参考。
梯度流:探索通向最小值之路
By 苏剑林 | 2023-06-16 | 40630位读者 | 引用在这篇文章中,我们将探讨一个被称为“梯度流(Gradient Flow)”的概念。简单来说,梯度流是将我们在用梯度下降法中寻找最小值的过程中的各个点连接起来,形成一条随(虚拟的)时间变化的轨迹,这条轨迹便被称作“梯度流”。在文章的后半部分,我们将重点讨论如何将梯度流的概念扩展到概率空间,从而形成“Wasserstein梯度流”,为我们理解连续性方程、Fokker-Planck方程等内容提供一个新的视角。
梯度下降
假设我们想搜索光滑函数f(\boldsymbol{x})的最小值,常见的方案是梯度下降(Gradient Descent),即按照如下格式进行迭代:
\begin{equation}\boldsymbol{x}_{t+1} = \boldsymbol{x}_t -\alpha \nabla_{\boldsymbol{x}_t}f(\boldsymbol{x}_t)\label{eq:gd-d}\end{equation}
如果f(\boldsymbol{x})关于\boldsymbol{x}是凸的,那么梯度下降通常能够找到最小值点;相反,则通常只能收敛到一个“驻点”——即梯度为0的点,比较理想的情况下能收敛到一个极小值(局部最小值)点。这里没有对极小值和最小值做严格区分,因为在深度学习中,即便是收敛到一个极小值点也是很难得的了。
SVD(Singular Value Decomposition,奇异值分解)是常见的矩阵分解算法,相信很多读者都已经对它有所了解,此前我们在《低秩近似之路(二):SVD》也专门介绍过它。然而,读者是否想到,SVD竟然还可以求导呢?笔者刚了解到这一结论时也颇感意外,因为直觉上“分解”往往都是不可导的。但事实是,SVD在一般情况下确实可导,这意味着理论上我们可以将SVD嵌入到模型中,并用基于梯度的优化器来端到端训练。
问题来了,既然SVD可导,那么它的导函数长什么样呢?接下来,我们将参考文献《Differentiating the Singular Value Decomposition》,逐步推导SVD的求导公式。
推导基础
假设\boldsymbol{W}是满秩的n\times n矩阵,且全体奇异值两两不等,这是比较容易讨论的情形,后面我们也会讨论哪些条件可以放宽一点。接着,我们设\boldsymbol{W}的SVD为:
\begin{equation}\boldsymbol{W} = \boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top}\end{equation}
【理解黎曼几何】4. 联络和协变导数
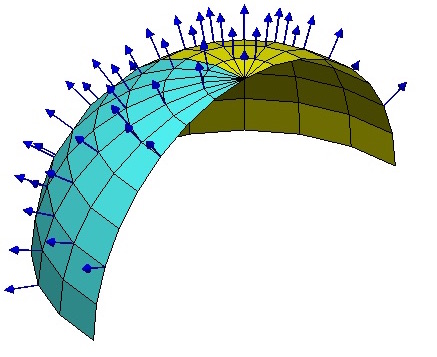
By 苏剑林 | 2016-10-16 | 91330位读者 | 引用向量与联络
当我们在我们的位置建立起自己的坐标系后,我们就可以做很多测量,测量的结果可能是一个标量,比如温度、质量,这些量不管你用什么坐标系,它都是一样的。当然,有时候我们会测量向量,比如速度、加速度、力等,这些量都是客观实体,但因为测量结果是用坐标的分量表示的,所以如果换一个坐标,它的分量就完全不一样了。
假如所有的位置都使用同样的坐标,那自然就没有什么争议了,然而我们前面已经反复强调,不同位置的人可能出于各种原因,使用了不同的坐标系,因此,当我们写出一个向量A^{\mu}时,严格来讲应该还要注明是在\boldsymbol{x}位置测量的:A^{\mu}(\boldsymbol{x}),只有不引起歧义的情况下,我们才能省略它。
到这里,我们已经能够进行一些计算,比如A^{\mu}是在\boldsymbol{x}处测量的,而\boldsymbol{x}处的模长计算公式为ds^2 = g_{\mu\nu} dx^{\mu} dx^{\nu},因此,A^{\mu}的模长为\sqrt{g_{\mu\nu} A^{\mu}A^{\nu}},它是一个客观实体。
泛化性乱弹:从随机噪声、梯度惩罚到虚拟对抗训练
By 苏剑林 | 2020-06-01 | 110822位读者 | 引用提高模型的泛化性能是机器学习致力追求的目标之一。常见的提高泛化性的方法主要有两种:第一种是添加噪声,比如往输入添加高斯噪声、中间层增加Dropout以及进来比较热门的对抗训练等,对图像进行随机平移缩放等数据扩增手段某种意义上也属于此列;第二种是往loss里边添加正则项,比如L_1, L_2惩罚、梯度惩罚等。本文试图探索几种常见的提高泛化性能的手段的关联。
随机噪声
我们记模型为f(x),\mathcal{D}为训练数据集合,l(f(x), y)为单个样本的loss,那么我们的优化目标是
\begin{equation}\mathop{\text{argmin}}_{\theta} L(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}}[l(f(x), y)]\end{equation}
\theta是f(x)里边的可训练参数。假如往模型输入添加噪声\varepsilon,其分布为q(\varepsilon),那么优化目标就变为
\begin{equation}\mathop{\text{argmin}}_{\theta} L_{\varepsilon}(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}, \varepsilon\sim q(\varepsilon)}[l(f(x + \varepsilon), y)]\end{equation}
当然,可以添加噪声的地方不仅仅是输入,也可以是中间层,也可以是权重\theta,甚至可以是输出y(等价于标签平滑),噪声也不一定是加上去的,比如Dropout是乘上去的。对于加性噪声来说,q(\varepsilon)的常见选择是均值为0、方差固定的高斯分布;而对于乘性噪声来说,常见选择是均匀分布U([0,1])或者是伯努利分布。
添加随机噪声的目的很直观,就是希望模型能学会抵御一些随机扰动,从而降低对输入或者参数的敏感性,而降低了这种敏感性,通常意味着所得到的模型不再那么依赖训练集,所以有助于提高模型泛化性能。
隐藏在动量中的梯度累积:少更新几步,效果反而更好?
By 苏剑林 | 2021-08-24 | 36877位读者 | 引用我们知道,梯度累积是在有限显存下实现大batch_size训练的常用技巧。在之前的文章《用时间换取效果:Keras梯度累积优化器》中,我们就简单介绍过梯度累积的实现,大致的思路是新增一组参数来缓存梯度,最后用缓存的梯度来更新模型。美中不足的是,新增一组参数会带来额外的显存占用。
这几天笔者在思考优化器的时候,突然意识到:梯度累积其实可以内置在带动量的优化器中!带着这个思路,笔者对优化了进行了一些推导和实验,最后还得到一个有意思但又有点反直觉的结论:少更新几步参数,模型最终效果可能会变好!
注:本文下面的结果,几乎原封不动且没有引用地出现在Google的论文《Combined Scaling for Zero-shot Transfer Learning》中,在此不做过多评价,请读者自行品评。
SGDM
在正式讨论之前,我们定义函数
\begin{equation}\chi_{t/k} = \left\{ \begin{aligned}&1,\quad t \equiv 0\,(\text{mod}\, k) \\
&0,\quad t \not\equiv 0\,(\text{mod}\, k)
\end{aligned}\right.\end{equation}
也就是说,t是一个整数,当它是k的倍数时,\chi_{t/k}=1,否则\chi_{t/k}=0,这其实就是一个t能否被k整除的示性函数。在后面的讨论中,我们将反复用到这个函数。
梯度视角下的LoRA:简介、分析、猜测及推广
By 苏剑林 | 2023-04-17 | 96720位读者 | 引用随着ChatGPT及其平替的火热,各种参数高效(Parameter-Efficient)的微调方法也“水涨船高”,其中最流行的方案之一就是本文的主角LoRA了,它出自论文《LoRA: Low-Rank Adaptation of Large Language Models》。LoRA方法上比较简单直接,而且也有不少现成实现,不管是理解还是使用都很容易上手,所以本身也没太多值得细写的地方了。
然而,直接实现LoRA需要修改网络结构,这略微麻烦了些,同时LoRA给笔者的感觉是很像之前的优化器AdaFactor,所以笔者的问题是:能否从优化器角度来分析和实现LoRA呢?本文就围绕此主题展开讨论。
方法简介
以往的一些结果(比如《Exploring Aniversal Intrinsic Task Subspace via Prompt Tuning》)显示,尽管预训练模型的参数量很大,但每个下游任务对应的本征维度(Intrinsic Dimension)并不大,换句话说,理论上我们可以微调非常小的参数量,就能在下游任务取得不错的效果。
LoRA借鉴了上述结果,提出对于预训练的参数矩阵W_0\in\mathbb{R}^{n\times m},我们不去直接微调W_0,而是对增量做低秩分解假设:
\begin{equation}W = W_0 + A B,\qquad A\in\mathbb{R}^{n\times r},B\in\mathbb{R}^{r\times m}\end{equation}








最近评论