层次分解位置编码,让BERT可以处理超长文本
By 苏剑林 | 2020-12-04 | 185199位读者 |大家都知道,目前的主流的BERT模型最多能处理512个token的文本。导致这一瓶颈的根本原因是BERT使用了从随机初始化训练出来的绝对位置编码,一般的最大位置设为了512,因此顶多只能处理512个token,多出来的部分就没有位置编码可用了。当然,还有一个重要的原因是Attention的$\mathcal{O}(n^2)$复杂度,导致长序列时显存用量大大增加,一般显卡也finetune不了。
本文主要面向前一个原因,即假设有足够多的显存前提下,如何简单修改当前最大长度为512的BERT模型,使得它可以直接处理更长的文本,主要思路是层次分解已经训练好的绝对位置编码,使得它可以延拓到更长的位置。
位置编码 #
BERT使用的是训练出来的绝对位置编码,这种编码方式简单直接,效果也很不错,但是由于每个位置向量都是模型自己训练出来的,我们无法推断其余位置的编码向量,因此有了长度限制。
解决这个问题的一个主流思路是换成相对位置编码,这是个可行的办法,华为的NEZHA模型便是一个换成了相对位置编码的BERT模型。相对位置编码一般会对位置差做个截断,使得要处理的相对位置都在一个有限的范围内,因此相对位置编码可以不受限于序列长度。但相对位置编码也不是完美的解决方案,首先像NEZHA那样的相对位置编码会增加计算量(如果是T5那种倒是不会),其次是线性Attention则没法用相对位置编码,也就是不够通用。
读者可能会想起《Attention is All You Need》不是提出了一种用$\sin,\cos$表示的Sinusoidal绝对位置编码吗?直接用那种不就不限制长度了?理论上是这样,但问题是目前没有用Sinusoidal位置编码的模型开放呀,难道我们还要自己从零训练一个?这显然不大现实呀~
层次分解 #
所以,在有限资源的情况下,最理想的方案还是想办法延拓训练好的BERT的位置编码,而不用重新训练模型。下面给出笔者构思的一种层次分解方案。
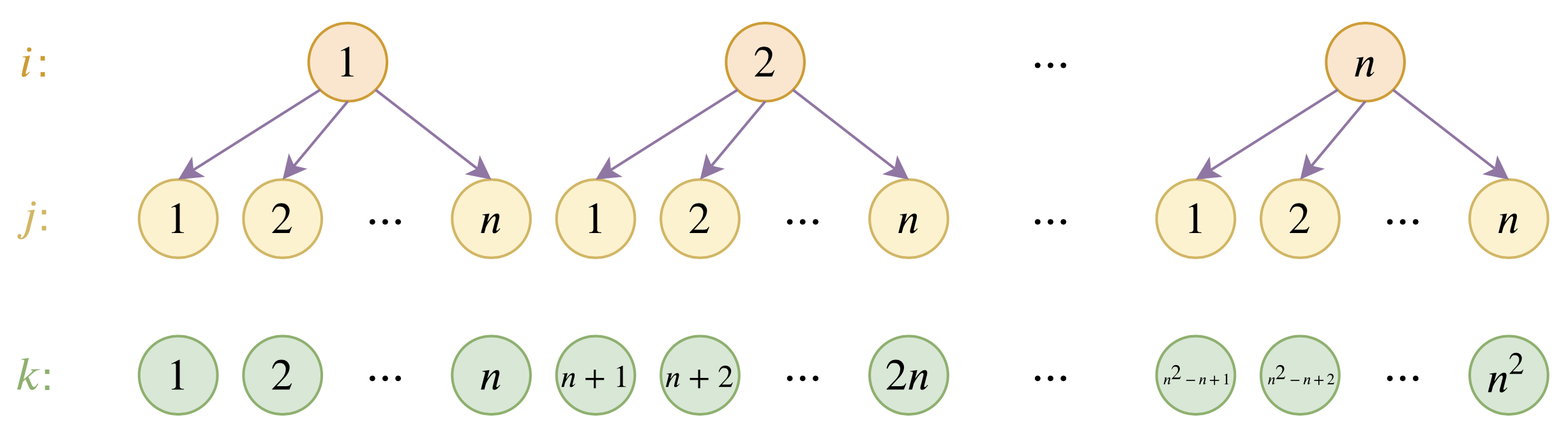
具体来说,假设已经训练好的绝对位置编码向量为$\boldsymbol{p}_1,\boldsymbol{p}_2,\cdots,\boldsymbol{p}_n$,我们希望能在此基础上构造一套新的编码向量$\boldsymbol{q}_1,\boldsymbol{q}_2,\cdots,\boldsymbol{q}_m$,其中$m > n$。为此,我们设
\begin{equation}\boldsymbol{q}_{(i-1)\times n + j} = \alpha \boldsymbol{u}_i + (1 - \alpha) \boldsymbol{u}_j\label{eq:fenjie}\end{equation}
其中$\alpha\in (0, 1)$且$\alpha\neq 0.5$是一个超参数,$\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_n$是该套位置编码的“基底”。这样的表示意义很清晰,就是将位置$(i - 1)\times n + j$层次地表示为$(i, j)$,然后$i, j$对应的位置编码分别为$\alpha \boldsymbol{u}_i$和$(1 - \alpha) \boldsymbol{u}_j$,而最终$(i - 1)\times n + j$的编码向量则是两者的叠加。要求$\alpha\neq 0.5$是为了区分$(i, j)$和$(j, i)$两种不同的情况。
我们希望在不超过$n$时,位置向量保持跟原来的一样,这样就能与已经训练好的模型兼容。换句话说,我们希望$\boldsymbol{q}_1=\boldsymbol{p}_1,\boldsymbol{q}_2=\boldsymbol{p}_2,\cdots,\boldsymbol{q}_n=\boldsymbol{p}_n$,这样就能反推出各个$\boldsymbol{u}_i$了:
\begin{equation}\boldsymbol{u}_i = \frac{\boldsymbol{p}_i - \alpha\boldsymbol{p}_1}{1 - \alpha},\quad i = 1,2,\cdots,n\end{equation}
这样一来,我们的参数还是$\boldsymbol{p}_1,\boldsymbol{p}_2,\cdots,\boldsymbol{p}_n$,但我们可以表示出$n^2$个位置的编码,并且前$n$个位置编码跟原来模型是相容的。
自我分析 #
事实上,读懂了之后,读者也许会觉得这个分解其实没什么技术含量,就是一个纯粹的拍脑袋的结果而已?其实确实是这样。
至于为什么会觉得这样做有效?一是由于层次分解的可解释性很强,因此可以预估我们的结果具有一定外推能力,至少对于大于$n$的位置是一个不错的初始化;二则是下一节的实验验证了,毕竟实验是证明trick有效的唯一标准。本质上来说,我们做的事情很简单,就是构建一种位置编码的延拓方案,它跟原来的前$n$个编码相容,然后还能外推到更多的位置,剩下的就交给模型来适应了。这类做法肯定有无穷无尽的,笔者只是选择了其中自认为解释性比较强的一种,提供一种可能性,并不是最优的方案,也不是保证有效的方案。
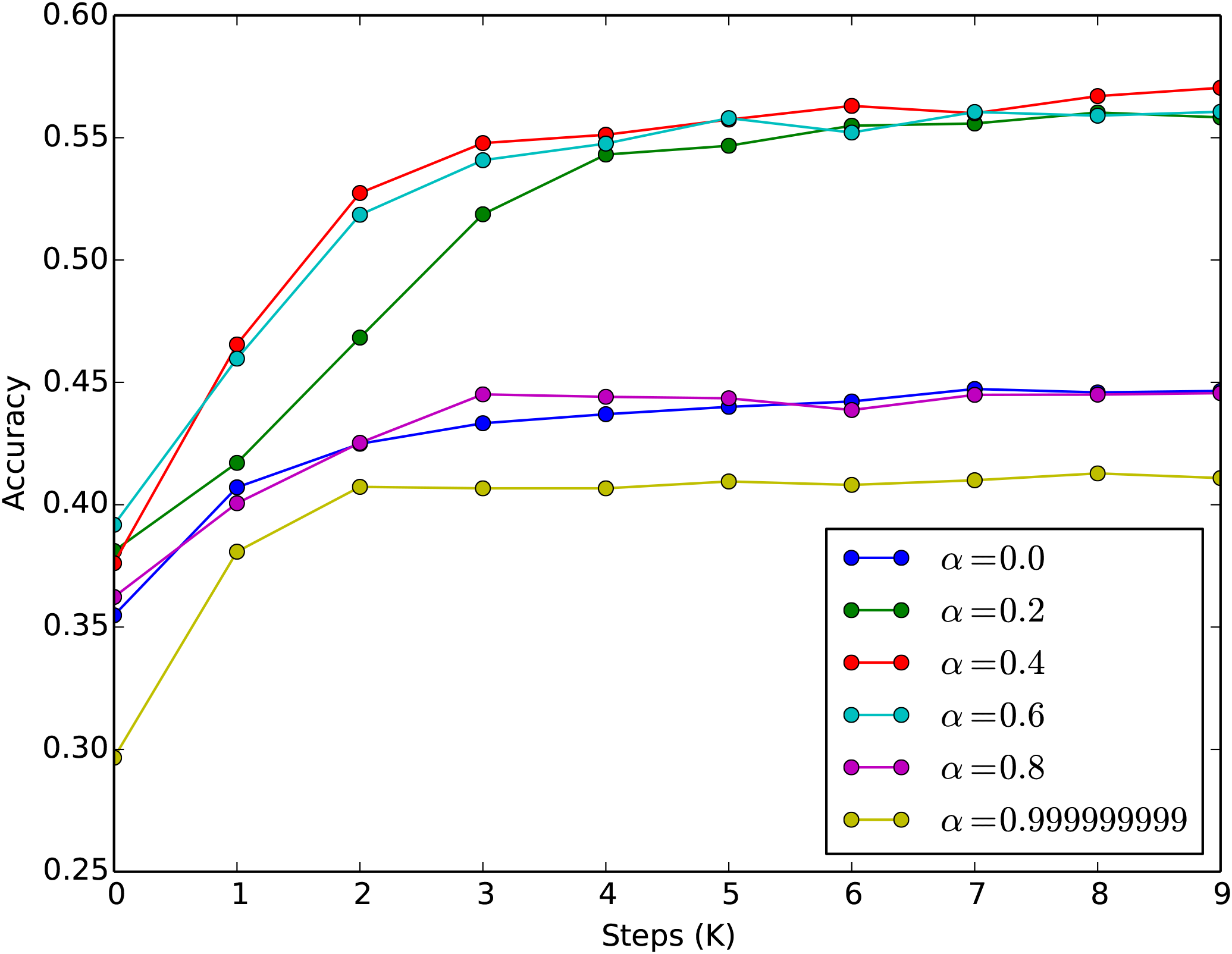
此外,讨论一下$\alpha$的选取问题,笔者默认的选择是$\alpha=0.4$。理论上来说,$\alpha\in (0, 1)$且$\alpha\neq 0.5$都成立,但是从实际情况出发,还是建议选择$0 < \alpha < 0.5$的数值。因为我们很少机会碰到上万长度的序列,对于个人显卡来说,能处理到2048已经很壕了,如果$n=512$,那么这就意味着$i = 1, 2, 3, 4$而$j=1,2,\cdots,512$,如果$\alpha > 0.5$的话,那么从分解式$\eqref{eq:fenjie}$看$\alpha \boldsymbol{u}_i$就会占主导,因次位置编码之间差异变小(因为$i$的候选值只有4个),模型不容易把各个位置区分开来,会导致收敛变慢;如果$\alpha < 0.5$,那么占主导的是$(1-\alpha) \boldsymbol{u}_j$,位置编码的区分度更好($j$的候选值有512个),模型收敛更快一些。
实践测试 #
综上所述,我们可以几乎无成本地延拓BERT的绝对位置编码,使得它最大长度可以达到$n^2=512^2=262144\approx 26\text{万}$!这绝对能满足我们的需求了吧?该改动已经内置在bert4keras>=0.9.5中,用户只需要在build_transformer_model中传入参数hierarchical_position=True即可启用,True也可以换为0~1之间的浮点数,代表上述$\alpha$的值,为True时则默认$\alpha=0.4$。
至于效果,笔者首先测了MLM任务,直接将最大长度设为1536,然后加载训练好的RoBERTa权重,发现MLM的准确率大概是38%左右(如果截断到512,那么大概是55%左右),经过finetune其准确率可以很快(3000步左右)恢复到55%以上。这个结果表明这样延拓出来的位置编码在MLM任务上是行之有效的。如果有空余算力的话,在做其他任务之前先在MLM下继续预训练一会应该是比较好的。同时,我们对不同的$\alpha$也做了实验,表明$\alpha=0.4$确实是一个不错的默认值,如下图所示。
然后测了两个长文本分类问题,分别将长度设为512和1024,其他参数不变进行finetune(直接finetune,没有先进行MLM继续预训练),其中一个数据集的结果没有什么明显变化;另一个数据集在验证集上1024的比512的要高0.5%左右。这再次表明本文所提的层次分解位置编码是能起作用的。所以,大家如果有足够显存的显卡,那就尽管一试吧,尤其是长文本的序列标注任务,感觉应该挺适合的。反正在bert4keras下就是多一行代码的事情,有提升就是赚到了,没提升也没浪费多少精力。欢迎大家报告自己的测试结果。
最后提供一个训练阶段最大长度与最大batch_size的参照表(RoBERTa Base版,24G的TITAN RTX):
$$\begin{array}{c|c}
\hline
\text{序列长度} & \text{batch_size}\\
\hline
512 & 22\\
1024 & 9\\
1536 & 5\\
\hline
\end{array}$$
从这个表中可以看到,其实序列长度翻一倍,显存占用量大约也就是翻一倍(多一点)而已,似乎跟传说中的$\mathcal{O}(n^2)$复杂度不一样?事实上,$\mathcal{O}(n^2)$是针对于足够长的序列的,这个“足够长”是指几千上万的,对于不超过2048的序列来说,其实BERT的复杂度还是近乎线性的,所以这种场景下直接用“BERT+延拓位置编码”的方式比“分句+BERT+LSTM”之类的设计要方便得多。
文章小结 #
本文分享了笔者构思的一种基于层次分解的位置编码延拓方案,通过这个延拓,BERT理论上最多可以处理长度达26万的文本,只要显存管够,就没有BERT处理不了的长文本。
所以,你准备好显存了吗?
转载到请包括本文地址:https://spaces.ac.cn/archives/7947
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 04, 2020). 《层次分解位置编码,让BERT可以处理超长文本 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/7947
@online{kexuefm-7947,
title={层次分解位置编码,让BERT可以处理超长文本},
author={苏剑林},
year={2020},
month={Dec},
url={\url{https://spaces.ac.cn/archives/7947}},
}










October 5th, 2023
想请问一下苏神,当albert的token长度设置为大于512时,总会报错tensorflow的维度准换问题。这与albert能处理的最大文本长度有关嘛?
Incompatible shapes: [1,512,128] vs. [32,528,128]
这与绝对位置编码有关。
March 17th, 2024
苏神您好,看完了你写的关于length extrapolation的文章。心中一直有一个疑问,positional embedding 完成之后,一般用什么方式来实现长度外推,使用滑动窗口吗?
你这个问题,怕是白看了“写的关于length extrapolation的文章”了...
May 7th, 2024
酱紫锐评哈哈哈
January 8th, 2025
有个问题想请教下苏神,本文通过层次分解法解决了长文本位置编码的问题,也就是长文本里超过固定长度(这里假设固定输入长度为512)的部分(比如513到1024位置)的input embedding可以求解出来,我的问题是,input embedding求出来后,输入模型,模型里相应的513~1024位置的矩阵权重怎么获取?备注:这里矩阵权重指的是 全连接权重,kqv参数权重等
长文本的模型的权重,是复制之前的模型权重吗,比如pos=513复制pos=1的模型权重
你可能还需要补习一下Transformer架构的细节,它不存在这个问题。
重新手推了一下,注意力wq wk wv矩阵维度确实与序列长度无关,确实不会存在这个问题。
February 24th, 2025
苏神,能不能请教下,为啥层次分解的基座要在原始的0-512位置的向量中做下变换呢?
如果动机只是为了初始化512-1024的向量,选择一个基座,然后层次分解。那么为啥这个基座不直接选择前512的(只初始化512-1024的向量),而是还要变化下呢?
是因为:这种层次分解能work的前提是,从0-1024点向量,必须是同一个基底?
先假设一种超过512的位置编码形式,然后用前512个已知的位置向量去拟合它呀,其实就是机器学习的思想,只不过这里追求完全拟合
March 4th, 2025
[...]层次分解位置编码,让BERT可以处理超长文本[...]