科学空间|Scientific Spaces

大家知道，从SimBERT到SimBERTv2（RoFormer-Sim），我们算是为中文文本相似度任务建立了一个还算不错的基准模型。然而，SimBERT和RoFormer-Sim本质上都只是“弱监督”模型，跟“无监督”类似，我们不能指望纯弱监督的模型能达到完美符合人的认知效果。所以，为了进一步提升RoFormer-Sim的效果，我们尝试了使用开源的一些标注数据来辅助训练。本文就来介绍我们的探索过程。

有的读者可能想：有监督有啥好讲的？不就是直接训练么？说是这么说，但其实并没有那么“显然易得”，还是有些“雷区”的，所以本文也算是一份简单的“扫雷指南”吧。

前情回顾

笔者发现，自从SimBERT发布后，读者问得最多的问题大概是：

为什么“我喜欢北京”跟“我不喜欢北京”相似度这么高？它们不是意思相反吗？

点击阅读全文...

我们知道，线性回归是比较简单的问题，它存在解析解，而它的变体逻辑回归（Logistic Regression）却没有解析解，这不能不说是一个遗憾。因为逻辑回归虽然也叫“回归”，但它实际上是用于分类问题的，而对于很多读者来说分类比回归更加常见。准确来说，我们说逻辑回归没有解析解，说的是“最大似然估计下逻辑回归没有解析解”。那么，这是否意味着，如果我们不用最大似然估计，是否能找到一个可用的解析解呢？

逻辑回归示意图

本文将会从非最大似然的角度，推导逻辑回归的一个解析解，简单的实验表明它效果不逊色于梯度下降求出来的最大似然解。此外，这个解析解还易于推广到单层Softmax多分类模型。

点击阅读全文...

在本博客中，我们已经多次讨论过线性Attention的相关内容。介绍线性Attention的逻辑大体上都是：标准Attention具有$\mathcal{O}(n^2)$的平方复杂度，是其主要的“硬伤”之一，于是我们$\mathcal{O}(n)$复杂度的改进模型，也就是线性Attention。有些读者看到线性Attention的介绍后，就一直很期待我们发布基于线性Attention的预训练模型，以缓解他们被BERT的算力消耗所折腾的“死去活来”之苦。

然而，本文要说的是：抱有这种念头的读者可能要失望了，标准Attention到线性Attention的转换应该远远达不到你的预期，而BERT那么慢的原因也并不是因为标准Attention的平方复杂度。

BERT之反思

按照直观理解，平方复杂度换成线性复杂度不应该要“突飞猛进”才对嘛？怎么反而“远远达不到预期”？出现这个疑惑的主要原因，是我们一直以来都没有仔细评估一下常规的Transformer模型（如BERT）的整体计算量。

点击阅读全文...

在《Performer：用随机投影将Attention的复杂度线性化》中我们了解到Google提出的Performer模型，它提出了一种随机投影方案，可以将标准Attention转化为线性Attention，并保持一定的近似。理论上来说，只要投影的维度足够大，那么可以足够近似标准Attention。换句话说，标准Attention可以视作一个无限维的线性Attention。

本文将介绍笔者构思的另外两种将标准Attention转换为无限维线性Attention的思路，不同于Performer的随机投影，笔者构思的这两种方案都是确定性的，并且能比较方便地感知近似程度。

简要介绍

关于标准Attention和线性Attention，这里就不多做介绍了，还不了解的读者可以参考笔者之前的文章《线性Attention的探索：Attention必须有个Softmax吗？》和《Transformer升级之路：3、从Performer到线性Attention》。简单来说，标准Attention的计算方式为
\begin{equation}a_{i,j}=\frac{e^{\boldsymbol{q}_i\cdot \boldsymbol{k}_j}}{\sum\limits_j e^{\boldsymbol{q}_i\cdot \boldsymbol{k}_j}}\end{equation}

点击阅读全文...

今天我们来学习Johnson-Lindenstrauss引理，由于名字比较长，下面都简称“JL引理”。

个人认为，JL引理是每一个计算机科学的同学都必须了解的神奇结论之一，它是一个关于降维的著名的结果，它也是高维空间中众多反直觉的“维度灾难”现象的经典例子之一。可以说，JL引理是机器学习中各种降维、Hash等技术的理论基础，此外，在现代机器学习中，JL引理也为我们理解、调试模型维度等相关参数提供了重要的理论支撑。

对数的维度

JL引理，可以非常通俗地表达为：

通俗版JL引理： 塞下$N$个向量，只需要$\mathcal{O}(\log N)$维空间。

点击阅读全文...

在五花八门的预训练任务设计中，NSP通常认为是比较糟糕的一种，因为它难度较低，加入到预训练中并没有使下游任务微调时有明显受益，甚至RoBERTa的论文显示它会带来负面效果。所以，后续的预训练工作一般有两种选择：一是像RoBERTa一样干脆去掉NSP任务，二是像ALBERT一样想办法提高NSP的难度。也就是说，一直以来NSP都是比较“让人嫌弃”的。

不过，反转来了，NSP可能要“翻身”了。最近的一篇论文《NSP-BERT: A Prompt-based Zero-Shot Learner Through an Original Pre-training Task--Next Sentence Prediction》（下面简称NSP-BERT）显示NSP居然也可以做到非常不错的Zero Shot效果！这又是一个基于模版（Prompt）的Few/Zero Shot的经典案例，只不过这一次的主角是NSP。

背景回顾

曾经我们认为预训练纯粹就是预训练，它只是为下游任务的训练提供更好的初始化，像BERT的预训练任务有MLM（Masked Language Model和NSP（Next Sentence Prediction），在相当长的一段时间内，大家都不关心这两个预训练任务本身，而只是专注于如何通过微调来使得下游任务获得更好的性能。哪怕是T5将模型参数训练到了110亿，走的依然是“预训练+微调”这一路线。

点击阅读全文...

在本系列的前面几篇文章中，我们已经从多个角度来理解了VAE，一般来说，用VAE是为了得到一个生成模型，或者是做更好的编码模型，这都是VAE的常规用途。但除了这些常规应用外，还有一些“小众需求”，比如用来估计$x$的概率密度，这在做压缩的时候通常会用到。

本文就从估计概率密度的角度来了解和推导一下VAE模型。

两个问题

所谓估计概率密度，就是在已知样本$x_1,x_2,\cdots,x_N\sim \tilde{p}(x)$的情况下，用一个待定的概率密度簇$q_{\theta}(x)$去拟合这批样本，拟合的目标一般是最小化负对数似然：
\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}[-\log q_{\theta}(x)] = -\frac{1}{N}\sum_{i=1}^N \log q_{\theta}(x_i)\label{eq:mle}\end{equation}

点击阅读全文...

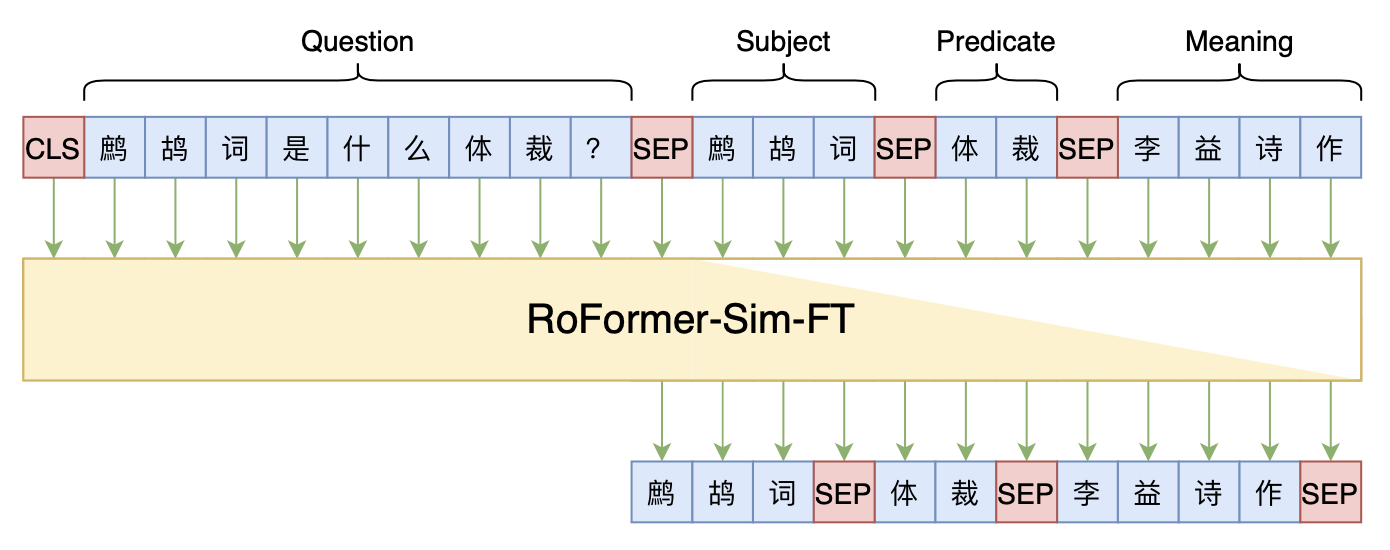
两年前，在《万能的seq2seq：基于seq2seq的阅读理解问答》和《“非自回归”也不差：基于MLM的阅读理解问答》中，我们在尝试过分别利用“Seq2Seq+前缀树”和“MLM+前缀树”的方式做抽取式阅读理解任务，并获得了不错的结果。而在去年的ICLR2021上，Facebook的论文《Autoregressive Entity Retrieval》同样利用“Seq2Seq+前缀树”的组合，在实体链接和文档检索上做到了效果与效率的“双赢”。

事实上，“Seq2Seq+前缀树”的组合理论上可以用到任意检索型任务中，堪称是检索任务的“新范式”。本文将再次回顾“Seq2Seq+前缀树”的思路，并用它来实现最近推出的KgCLUE知识图谱问答榜单的一个baseline。

本文baseline模型示意图

点击阅读全文...