科学空间|Scientific Spaces

新的《量子力学与路径积分》习题解答又放出来啦。与前两个版本不同的是，前两次更新，每次基本上完成了两章的习题，而这一次，只是增加了第6章的22道习题（第6章共有29道）。原因很多，各种忙就不说啦，主要是第6章开始，各种题目开始复杂起来，计算量也增大，虽然笔者是数学系的，可是还是前进得艰难。还有，第4、5两章加起来也只是25道习题，第6章却有29题，因此，本次更新的工作量，远远大于前两次更新的工作量。

为什么只有22题？当然是没有做完啦。为什么没有做完就更新啦？因为笔者觉得右面的题目，跟第7章的联系更为密切，因此，怕读者等不及，所以剩下的题目，跟第7章一起再发吧。

此外，我是看着中文版来做题的，中文版的翻译质量还不错，但是细微之处却有些不妥当，所以笔者要来回参考中英文版，颇累。读者可以发现，这一版中，“勘误”增加了不少。

点击阅读全文...

由于在实习中，事情比较多，做题时间比较少。并且越往后题目难度越大，因此习题解答的更新速度也慢了。现在是0.2版本，基本完成了前五章的习题，并且整理了版面，还加入了新版《量子力学与路径积分》的勘误。

如有问题，请指出，谢谢。

下载：《量子力学与路径积分》习题解答V0.2.pdf

忘了告诉大家，笔者是师范生，目前大四了，按照计划，我已经在一所高中实习了，因此，这两个月更新可能不怎么多，回复也不及时，请大家见谅。

趁这两个月时间，每天做一点《量子力学与路径积分》中的习题，整理与大家分享。目前是V0.1版，暂时只有第二三章的大部分习题解答。

点击阅读全文...

ODE的坐标变换

熟悉理论力学的读者应该能够领略到变分法在变换坐标系中的作用。比如，如果要将下面的平面二体问题方程
$$\left\{\begin{aligned}\frac{d^2 x}{dt^t}=\frac{-\mu x}{(x^2+y^2)^{3/2}}\\
\frac{d^2 y}{dt^t}=\frac{-\mu y}{(x^2+y^2)^{3/2}}\end{aligned}\right.\tag{1}$$
变换到极坐标系下，如果直接代入计算，将会是一道十分繁琐的计算题。但是，我们知道，上述方程只不过是作用量
$$S=\int \left[\frac{1}{2}\left(\dot{x}^2+\dot{y}^2\right)+\frac{\mu}{\sqrt{x^2+y^2}}\right]dt\tag{2}$$
变分之后的拉格朗日方程，那么我们就可以直接对作用量进行坐标变换。而由于作用量一般只涉及到了一阶导数，因此作用量的变换一般来说比较简单。比如，很容易写出，$(2)$在极坐标下的形式为
$$S=\int \left[\frac{1}{2}\left(\dot{r}^2+r^2\dot{\theta}^2\right)+\frac{\mu}{r}\right]dt\tag{3}$$
对$(3)$进行变分，得到的拉格朗日方程为
$$\left\{\begin{aligned}&\ddot{r}=r\dot{\theta}^2-\frac{\mu}{r^2}\\
&\frac{d}{dt}\left(r^2\dot{\theta}\right)=0\end{aligned}\right.\tag{4}$$
就这样完成了坐标系的变换。如果想直接代入$(1)$暴力计算，那么请参考《方程与宇宙》:二体问题的来来去去(一)

点击阅读全文...

我小时候一直有个疑问：

直升机上的螺旋桨能不能用来挡雨？

一般的螺旋桨是若干个“条状”物通过旋转对称而形成的，也就是说，它并非一个面，按常理来说，它是没办法用来挡雨的。但是，如果在高速旋转的情况下，甚至假设旋转速度可以任意大，那么我们任意时刻都没有办法穿过它了，这种情况下，它似乎与一个实在的面无异？

力的无穷分解

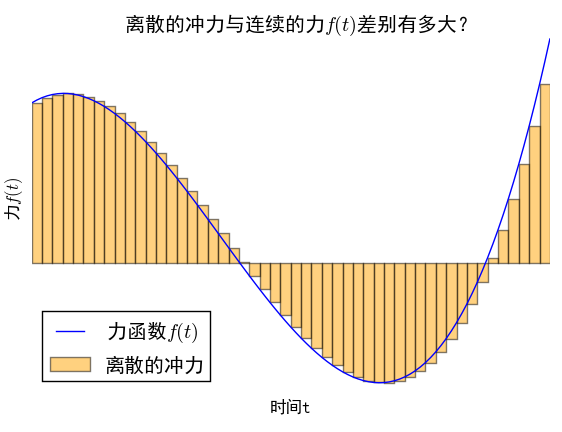
当然，以上只是笔者小时候的一个“异想天开”的念头，读者不必较真。不过，这个疑问跟本文有什么联系呢？我们在研究振动问题之时，通常会遇到在变力的作用下的受迫振动问题，已知变力是时间的函数，比如$f(t)$，然而，虽然知道$f(t)$的具体形式，但是由于$f$的非线性性，加上外力之后的运动，不一定容易求解。然而，如果可以将一个变化的力分段为无数个无穷小时间内的恒力（冲力），那么我们就可以分段讨论我们要研究的运动，而通常来说，恒力的问题会比变力容易。将一个变力离散化，然后再取极限，那么是不是跟原来在变力下的运动是一样的呢？这跟文章开头的疑问有着类似的思想——离线的极限，跟连续本身，是不是等价的？

而让人惊喜的是，在通常的物理系统中，将力分段为无数个小区间内的恒力的做法，能够导致正确的答案，而且，这恰好是线性常微分方程的格林函数法。下面我们来分析这一做法。

点击阅读全文...

最近的很多篇文章都是数论内容，属于纯数学的范畴了，对于很多只爱好物理或应用数学的读者可能会看得头晕了。今天我们来谈些不那么抽象的东西，我们来谈谈风筝，并来分析一下风筝的飞行力学。

爱情就像放风筝，线不能来得太紧，也不能拉得太松，你只会给对方飞翔的空间，他/她始终会回到你身边，因为有一条线系着双方。

风筝，在我们这个地方叫做纸鸢，相信大家童年时一定会放过。笔者小时候放风筝时，已经是小学五年级之前的事了。这个暑假突然童心一起，凭着小时候的回忆，简单做了个风筝来玩，居然真的飞起来了！兴奋之余，与大家分享一下。如今再来放风筝，真心感觉到放风筝也有很多技巧，让风筝飞，还不是件容易的事情呢，真可谓人生处处皆学问呀。上面关于风筝的比喻，正是放风筝的真实写照吧。

风筝可以说是人类摆脱地球重力的最原始尝试吧，跟发射宇宙飞船的火箭不同，风筝是借助风力来抵抗重力，严格来讲，即便是现在的飞机，也离不开这个原理（我们最后会谈到）。简单来讲，风筝就是用轻的支架撑开一个轻盈的平面，然后系上一个线圈。我们简单做一个风筝，只需要一张报纸，两条竹篾和一点透明胶，十分钟内就可以完成一个。当然，现在已经有各种各样的好看的风筝，甚至还有龙形的风筝，但是，自己动手简单做一个风筝，还是相当好玩的。

风筝自然是借助风力飞起来的，可是为什么风筝得用绳子牵着才能飞得更高、绳断了反而掉下来？风大多时，才适合放风筝？飞机又是怎么飞起来的？下面我们试着分析这些问题。

点击阅读全文...

从这个系列的第一篇文章到本文，已经隔了好多天。其实本文的内容是跟第一篇的内容同时完成的，为什么这么久才更新呢？原因有二，其一是随着春天的到来人也开始懒起来了，颓废呀～；其二，我在思考着规范变换的问题。按照朗道《场论》的逻辑，发展完质点力学理论后，下一步就是发展场论，诸如电磁场、引力场等。但是场论中有个让我比较困惑的东西，即场论存在着“规范不变性”。按照一般观点，我们是将规范不变性看作是电磁场方程的一个结果，即推导出电磁场的方程后，“发现”它具有规范不变性。但是如果用本文的方法，即假定场有这种对称性，然后就可以构建出场方程了。可是，为什么场存在着规范不变性，我还未能思考清楚。据我阅读到的资料来看，这个不变性似乎跟广义不变性有关（电磁场也是，这似乎说明即使在平直时空的电磁场理论中也暗示了广义不变性？）。还有，似乎这个不变性需要在量子场论中才能得到比较满意的解释，可是这样的话，就离我还很远了。

好吧，我们还是先回到相对论力学的推导中。

“无”中生有

上一篇文章我们已经构建了相对论力学的无穷小生成元，并进行了延拓。我已经说过，仅需要无穷小的变换形式，就可以构建出完成的相对论力学定律出来（当然这需要一些比较“显然”的假设）。这是个几乎从“无”到有的过程，也是本文标题的含义所在。另一方面，这种从局部到整体的可能性，也给我们带来一些启示：假如方法是普适的，那么可以由此构造出我们需要的物理定律来，包括电磁场、引力场方程等。（当然，我离这个目标还有点远。）

点击阅读全文...

本文很荣幸得到了高教社的王超编辑（新浪微博 @朗道集结号 ）在微信上的推荐，在此表示十分的感谢。

朗道集结号
朗道、费曼、薛定谔、泡利、狄拉克、温伯格……大师在这里等着你，微信号：ldjjhwx

事实上，取这个标题，有点狂妄自大、班门弄斧的感觉。原因之一是我自己并非物理专业学生，也没有学好物理。再者，我自己也没有读过多少费曼和朗道的书，谈不上“饱读”费曼朗道，又何以指导大家呢？

但是，结合自己在阅读他们的著作的感受，以及自己学习科学的过程，谈谈我对他们的著作的看法。

什么才是最简洁的方式？

相信不少读者觉得朗道的教程比费曼的讲义要深，感觉朗道的书总有大量的数学公式，而费曼的书则轻松一些。笔者开始也有这样的感觉，但是慢慢读下去，才感到费曼的书甚至比朗道的困难。

在进入讨论之前，我们不妨先想一下：什么才是理解物理的最简洁方式？数学越复杂，就越不好吗？

点击阅读全文...