Transformer升级之路：7、长度外推性与局部注意力

对于Transformer模型来说，其长度的外推性是我们一直在追求的良好性质，它是指我们在短序列上训练的模型，能否不用微调地用到长序列上并依然保持不错的效果。之所以追求长度外推性，一方面是理论的完备性，觉得这是一个理想模型应当具备的性质，另一方面也是训练的实用性，允许我们以较低成本（在较短序列上）训练出一个长序列可用的模型。

下面我们来分析一下加强Transformer长度外推性的关键思路，并由此给出一个“超强基线”方案，然后我们带着这个“超强基线”来分析一些相关的研究工作。

思维误区 #

第一篇明确研究Transformer长度外推性的工作应该是ALIBI，出自2021年中期，距今也不算太久。为什么这么晚（相比Transformer首次发表的2017年）才有人专门做这个课题呢？估计是因为我们长期以来，都想当然地认为Transformer的长度外推性是位置编码的问题，找到更好的位置编码就行了。

事实上，通过对比现有的一些位置编码的外推效果，确实能找到支撑该观点的一些论据。比如后面分享的多篇实验效果显示，相对位置编码的长度外推性，平均好于绝对位置编码的；像RoPE这样的函数式相对位置编码，又会比训练式相对位置编码的外推效果好些。所以看上去，似乎只要我们不断优化位置编码形式，最终就能给Transformer提供更好的长度外推性，从而解决这个问题。然而，情况没有那么乐观，像RoPE算是外推能力较好的位置编码，也只能外推10%到20%左右的长度而保持效果不变差，再长效果就会骤降。这个比例与预期差太远了，设想中好歹能外推个几倍长度才算是有价值的外推，所以不难想象，单靠改进位置编码改进Transformer的长度外推性，就不知道要等多久才能实现更长的效果了。

在直觉上，相信很多读者觉得像Sinusoidal或RoPE之类的函数式位置编码，它们没有训练参数，长度外推性应该很好才对，但事实上并非如此，这类位置编码并没有在长度外推方面表现出什么优势。为什么会这样呢？其实是大家在假设函数式位置编码的外推性时，忘了它的基本前提——“光滑性”。

其实，外推性就是局部推断整体，对此我们应该并不陌生，泰勒级数近似就是经典的例子，它只需要知道函数某点处若干阶导数的值，就可以对一个邻域内的值做有效估计，它依赖的就是给定函数的高阶光滑性（高阶导数存在且有界）。但是Sinusoidal或RoPE是这种函数吗？并不是。它们是一系列正余弦函数的组合，其相位函数是$k/10000^{2i/d}$，当$2i/d\approx 0$时，函数近似就是$\sin k, \cos k$，这算是关于位置编码$k$的高频振荡函数了，而不是直线或者渐近趋于直线之类的函数，所以基于它的模型往往外推行为难以预估。能否设计不振荡的位置编码？很难，位置编码函数如果不振荡，那么往往缺乏足够的容量去编码足够多的位置信息，也就是某种意义上来说，位置编码函数的复杂性本身也是编码位置的要求。

超强基线 #

事实上，更准确的定位应该是：

长度外推性是一个训练和预测的长度不一致的问题。

具体来说，不一致的地方有两点：

1、预测的时候用到了没训练过的位置编码（不管绝对还是相对）；

2、预测的时候注意力机制所处理的token数量远超训练时的数量。

第1点可能大家都容易理解，没训练过的就没法保证能处理好，这是DL中很现实的现象，哪怕是Sinusoidal或RoPE这种函数式位置编码也是如此。关于第2点，可能读者会有些迷惑，Attention理论上不就是可以处理任意长度的序列吗？训练和预测长度不一致影响什么呢？答案是熵，我们在《从熵不变性看Attention的Scale操作》也已经分析过这个问题，越多的token去平均注意力，意味着最后的分布相对来说越“均匀”（熵更大），即注意力越分散；而训练长度短，则意味着注意力的熵更低，注意力越集中，这也是一种训练和预测的差异性，也会影响效果。

事实上，对于相对位置编码的Transformer模型，通过一个非常简单的Attention Mask，就可以一次性解决以上两个问题，并且取得接近SOTA的效果：

超强基线模型（双向注意力版）

超强基线模型（单向注意力版）

不难理解，这就是将预测时的Attention变为一个局部Attention，每个token只能看到训练长度个token。这样一来，每个token可以看到的token数跟训练时一致，这就解决了第2个问题，同时由于是相对位置编码，位置的计数以当前token为原点，因此这样的局部Attention也不会比训练时使用更多的未知编码，这就解决了第1个问题。所以，就这个简单的Attention Mask一次性解决了长度外推的2个难点，还不用重新训练模型，更令人惊叹的是，各种实验结果显示，如果以它为baseline，那么各种同类工作的相对提升就弱得可怜了，也就是它本身已经很接近SOTA了，可谓是又快又好的“超强基线”。

论文学习 #

自ALIBI起，确实已经有不少工作投入到了Transformer长度外推性的研究中。在这一节中，笔者学习并整理了一下其中的一些代表工作，从中我们也可以发现，它们基本都跟基线模型有着诸多相通之处，甚至可以说它们某种程度上都是基线模型的变体，由此我们将进一步体会到长度外推性与注意力的局部性之间的深刻联系。

ALIBI #

作为“开山之作”，ALIBI是绕不过去的，它出自论文《Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation》。事后来看，ALIBI所做的改动非常简单，只是在Softmax之前，将Attention的计算从$\boldsymbol{q}_m^{\top}\boldsymbol{k}_n$改为
\begin{equation}\boldsymbol{q}_m^{\top}\boldsymbol{k}_n - \lambda|m - n|\label{eq:alibi}\end{equation}
其中$\lambda > 0$是超参数，每个head设置不同的值。从这个定义就可以看出ALIBI跟基线模型的相似之处了，两者都是在Softmax之前减去一个非负矩阵，只不过被减去的非负矩阵有所不同，ALIBI可以看成是基线模型的“光滑版”：

基线模型所减去的矩阵

ALIBI所减去的矩阵

ALIBI是一个很朴素（当然也很有效）的光滑局部注意力技巧，但如果将它理解为“位置编码”，那么应该是不大妥当的，如果就按照式$\eqref{eq:alibi}$来推广到双向注意力，那么由于$|m - n|=|n - m|$，按理说模型就无法区分“左”和“右”，只能识别相对距离的远近，显然是无法准确识别位置信息的。至于它在单向语言模型上效果好，是因为单向语言模型即便不加任何位置编码也能取得非平凡的效果（明显高于随机），ALIBI所施加的局部注意力，起到的是增强局域性的作用，贴合语言模型任务本身的特性。

KERPLE #

KERPLE出自论文《KERPLE: Kernelized Relative Positional Embedding for Length Extrapolation》，它实质上就是ALIBI的简单推广，它引入了两个训练参数$r_1,r_2$来一般化式$\eqref{eq:alibi}$：
\begin{equation}\left\{\begin{aligned}&\boldsymbol{q}_m^{\top}\boldsymbol{k}_n - r_1|m - n|^{r_2} ,\qquad\qquad r_1 >0, 0 < r_2 \leq 2\\
&\boldsymbol{q}_m^{\top}\boldsymbol{k}_n - r_1\log(1+r_2|m - n|),\qquad\qquad r_1, r_2 > 0
\end{aligned}\right.\label{eq:kerple}\end{equation}
又是一般化，又有可训练参数，KERPLE能取得比ALIBI更好的效果并不让人意外。不过这里要严重批评一下KERPLE论文的故弄玄虚，按照排版，原论文第三节是论文的理论支撑，但很明显它只是为了强行提高文章的数学深度而引入的无关篇幅，实质上对理解KERPLE毫无帮助，甚至会降低读者的阅读兴致（说白了，为审稿人服务，不是为读者服务）。

Sandwich #

Sandwich也是KERPLE的作者们搞的，出自《Receptive Field Alignment Enables Transformer Length Extrapolation》，上个月才放到Arxiv上的，它将式$\eqref{eq:alibi}$替换为
\begin{equation}\boldsymbol{q}_m^{\top}\boldsymbol{k}_n + \lambda\boldsymbol{p}_m^{\top}\boldsymbol{p}_n\label{eq:sandwich}\end{equation}
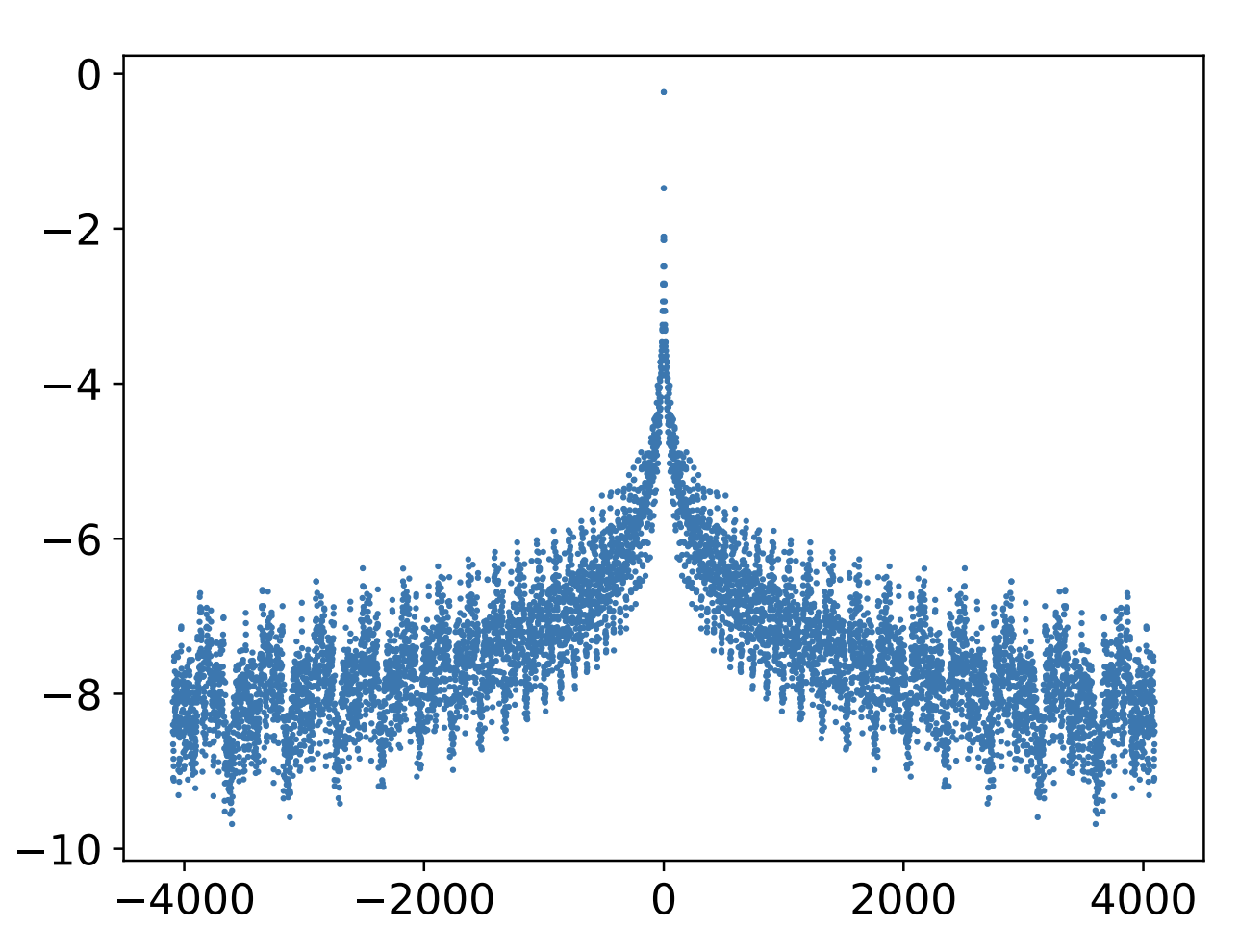
其中$\boldsymbol{p}_m,\boldsymbol{p}_n$是Sinusoidal位置编码，$\lambda > 0$是超参数。从《Transformer升级之路：1、Sinusoidal位置编码追根溯源》我们知道，$\boldsymbol{p}_m^{\top}\boldsymbol{p}_n$是$m-n$的标量函数，并且平均而言是$|m-n|$的单调递增函数，所以它的作用也跟$-\lambda|m-n|$相似。之所以强调“平均而言”，是因为$\boldsymbol{p}_m^{\top}\boldsymbol{p}_n$整体并非严格的单调，而是振荡下降，如图所示：

dot(p_m, p_n) 的函数图像（减去了d/2）

如果有必要，我们也可以将Sandwich转换成RoPE那样“绝对位置编码实现相对位置编码”的形式，这只需要留意到
\begin{equation}\boldsymbol{q}_m^{\top}\boldsymbol{k}_n + \lambda\boldsymbol{p}_m^{\top}\boldsymbol{p}_n = \left[\boldsymbol{q}_m, \sqrt{\lambda}\boldsymbol{p}_m\right]^{\top}\left[\boldsymbol{k}_n, \sqrt{\lambda}\boldsymbol{p}_n\right]\end{equation}
也就是说Sandwich通过拼接的方式补充绝对位置信息，其Attention结果则相当于相对位置编码。不过目前看来这个转换也就只有理论价值，因为拼接增加了向量维度，反而会进一步增加Attention的计算量。

XPOS #

XPOS出自论文《A Length-Extrapolatable Transformer》，跟Sandwich同一天出现在Arxiv上，它是RoPE的一个一脉相承的推广。我们知道，RoPE的基本解是：
\begin{equation}\boldsymbol{q}_m\to \boldsymbol{\mathcal{R}}_m\boldsymbol{q}_m,\quad \boldsymbol{k}_n\to \boldsymbol{\mathcal{R}}_n\boldsymbol{k}_n\end{equation}
其中$\boldsymbol{\mathcal{R}}_n=\begin{pmatrix}\cos n\theta & -\sin n\theta\\ \sin n\theta & \cos n\theta\end{pmatrix}$。笔者当时推导RoPE的时候，假设了“$Q$、$K$做同样的变换”，事实上单从“绝对位置实现相对位置”角度来看，并没有必要限制两者的变换格式一致，比如XPOS考虑的是
\begin{equation}\boldsymbol{q}_m\to \boldsymbol{\mathcal{R}}_m\boldsymbol{q}_m \xi^m,\quad \boldsymbol{k}_n\to \boldsymbol{\mathcal{R}}_n\boldsymbol{k}_n \xi^{-n}\end{equation}
其中$\xi$是一个标量超参，这样以来
\begin{equation}(\boldsymbol{\mathcal{R}}_m\boldsymbol{q}_m \xi^m)^{\top}(\boldsymbol{\mathcal{R}}_n\boldsymbol{k}_n \xi^{-n}) = \boldsymbol{q}_m^{\top}\boldsymbol{\mathcal{R}}_{n-m}\boldsymbol{k}_n \xi^{m-n}\end{equation}
总的结果依然是只依赖于相对位置$m-n$的。然而，现在问题是指数部分是$m-n$而不是$|m-n|$，只要$\xi\neq 1$，那么总有一边是发散的。XPOS的机智之处是它选择了跟很多相关工作一样选定了场景——只关注单向语言模型——这样一来我们只会用到$m\geq n$部分的注意力！此时只需要选择$\xi\in(0,1)$，就可以实现随着相对距离衰减的效果。

事实上，额外引入的指数衰减项$\xi^m$并非XPOS的首创，笔者所阅读的文献中，同样的项最早出现在PermuteFormer中，只不过PermuteFormer主要关心的是线性Attention场景。细节上，XPOS给每个分块都分配了不同的$\xi$，但在跟作者私下交流的时候，作者补做了共享同一个$\xi$的实验，发现设置不同$\xi$带来的提升几乎可以忽略。另外，我们要适当控制$\xi$的值，以防止$\xi^{-n}$在$n$较大的时候溢出。

值得指出的是，这里的随着相对距离衰减，是直接乘在Softmax之前的Attention Score的，结果是相对距离较远的Score变得很接近于0，而不是像前面几种设计那样趋向负无穷。$e^0$并没有趋于零的效果，所以说，这样的设计并非是局部Attention的变体，因此它的效果没有达到SOTA。为弥补这部分差距，XPOS设计了一个特殊的局部Attention（称为Blockwise Causal Attention，简写BCA），加上去之后就能够补足这个差距了。在交流时作者表示使用BCA是因为在实现上有优势，实际上基线模型的局部Attention效果更好，所以，要外推性还是要看局部注意力啊。

原论文的实验还是很丰富很值得参考的，建议大家细读～

文章小结 #

本文总结了增强Transformer的长度外推能力的相关工作，其中包含了一个简单但强大的基线方案，以及若干篇聚焦于长度外推性的相关工作，从中我们可以发现，这些工作本质上都是基线方案——局部注意力的变体，局部注意力是长度外推的关键环节之一。

转载到请包括本文地址：https://spaces.ac.cn/archives/9431

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。