蘑菇的最优形状模型
By 苏剑林 | 2011-04-30 | 61637位读者 |达尔文的进化学说告诉我们,自然界总是在众多的生物中挑出最能够适应环境的物种,赋予它们更高的生存几率,久而久之,这些物种经过亿万年的“优胜劣汰”,进化成了今天的千奇百怪的生物。无疑,经过长期的选择,优良的形状会被累积下来,换句话讲,这些物种在某些环境适应能力方面已经达到最优或近乎最优的状态(又是一个极值问题了)。好,现在我们来考虑蘑菇。
蘑菇是一种真菌生物,一般生长在阴暗潮湿的环境中。喜欢湿润的它自然也不希望散失掉过多的水分,因此,它努力地调整自身的形状,使它的“失水”尽可能地少。假设单位面积的蘑菇的失水速度是一致的,那么问题就变成了使一个给定体积的立体表面积尽可能少的问题了。并且考虑到水平各向同性生长的问题,理想的蘑菇形状应该就是一个平面图形的旋转体。那么这个旋转体是什么呢?聪明的你是否想到了是一个球体(的一部分)呢?
不过很遗憾,答案并非球体。我们来分析下这个问题,即哪种曲线的旋转体表面积最小,该曲线过$(x_1,y_1)$和$(x_2,y_2)$。
若已知曲线$y=f(x)$是满足条件的曲线,由于两个底面都是已知面积的圆,我们只需要考虑侧面积。旋转体的侧面积计算公式为:
$$\begin{aligned}S=\int_{x_1}^{x_2} 2\pi x\sqrt{dx^2+dy^2} \\ =2\pi\int_{x_1}^{x_2} x\sqrt{1+\dot{y}^2}dx\end{aligned}$$
这里$\dot{y}=\frac{dy}{dx}$。上述式子的意思就是将立体无限分割,将每一部分的立体当成一个圆台,用圆台的侧面积近似代替,并累积。
至此,问题变成了求一个函数$y=f(x)$使得积分$S=2\pi\int_{x_1}^{x_2} x\sqrt{1+\dot{y}^2}dx$取极值。根据欧拉-拉格朗日方程,应该有
$$\frac{d}{dx}\left(\frac{\partial \left(x\sqrt{1+\dot{y}^2}\right)}{\partial \dot{y}}\right)=\frac{\partial \left(x\sqrt{1+\dot{y}^2}\right)}{\partial y}=0$$
所以有$\frac{\partial (x\sqrt{1+\dot{y}^2})}{\partial \dot{y}}=\frac{x\dot{y}}{\sqrt{1+\dot{y}^2}}=C_1$,C1是积分常数。继而能够推出
$$\dot{y}=C_1\sqrt{\frac{1}{x^2-C_1^2}}$$
这时候,只要两边积分就可以得到:$y=C_1 ln\left|x+\sqrt{x^2-C_1^2}\right|+C_2$。或者利用双曲函数改写成
$$x=C_1 \cosh\left(\frac{y-C_2}{C_1}\right)$$
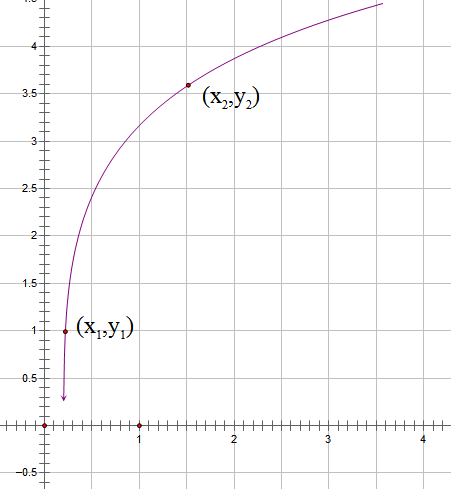
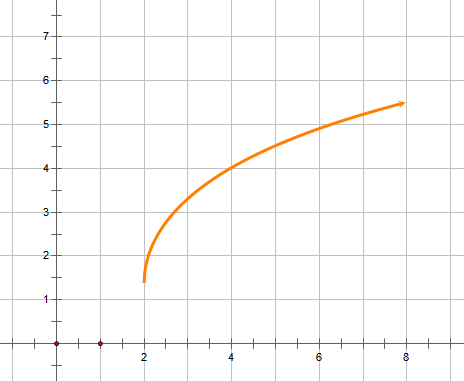
可见,这并不是一个圆。这是一个怎样的形状呢?如果设$C_1=2,C_2=0$,则利用几何画板可以画出
显然,该形状还是比较接近的。另一方面,双曲函数包含着自然对数的底e这个神奇的常数,也就是说,e本来源于自然,也充分体现着自然!这是一个多么和谐的世界!
转载到请包括本文地址:https://spaces.ac.cn/archives/1339
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Apr. 30, 2011). 《蘑菇的最优形状模型 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1339
@online{kexuefm-1339,
title={蘑菇的最优形状模型},
author={苏剑林},
year={2011},
month={Apr},
url={\url{https://spaces.ac.cn/archives/1339}},
}











May 6th, 2011
太酷了,这是什么书上的啊,推荐下
对了,忘了提一下:问题来源自《微分方程与数学物理问题》 By 伊布拉基莫夫(Nail H.Ibragimov)。个人感觉这是一本有关微分方程很好的书。现行的绝大多数微分方程书籍讲的都是定性理论,而该书则介绍了如何通过对称分析(李群)来求微分方程的精确解析解(即定量理论,当然前提是方程可积,因此李群也可以给出了判断方程是否可积的条件,当然此书的绝大多数内容我都看不懂),而群论是求积微分方程的最有效方法。
当然,关于微分方程还有另外一类书籍,即求微分方程的近似解之类的书,我复印了一本叫《微分方程的近似解法》的,不过也没有太多时间和心思去研究(又是一种浪费....^_^)
December 28th, 2011
e常数是怎么产生的?
是1+1/1+1/(2*1)+1/(3*2*1)+1/(4*3*2*1)+……这个算式的极限,大约是2.718281828。
January 21st, 2020
哈哈,有意思
July 11th, 2024
有意思,