n维空间下两个随机向量的夹角分布

昨天群里大家讨论到了$n$维向量的一些反直觉现象，其中一个话题是“一般$n$维空间下两个随机向量几乎都是垂直的”，这就跟二维/三维空间的认知有明显出入了。要从理论上认识这个结论，我们可以考虑两个随机向量的夹角$\theta$分布，并算算它的均值方差。

概率密度 #

首先，我们来推导$\theta$的概率密度函数。呃，其实也不用怎么推导，它是$n$维超球坐标的一个直接结论。

要求两个随机向量之间的夹角分布，很显然，由于各向同性，所以我们只需要考虑单位向量，而同样是因为各向同性，我们只需要固定其中一个向量，考虑另一个向量随机变化。不是一般性，考虑随机向量为
\begin{equation}\boldsymbol{x}=(x_1,x_2,\dots,x_n)\end{equation}
而固定向量为
\begin{equation}\boldsymbol{y}=(1,0,\dots,0)\end{equation}

将$\boldsymbol{x}$变换为超球坐标（关于$n$维球的知识可以参考维基百科）：
\begin{equation}
\left\{\begin{aligned}
x_{1}&=\cos(\varphi_{1})\\
x_{2}&=\sin(\varphi_{1})\cos(\varphi_{2})\\
x_{3}&=\sin(\varphi_{1})\sin(\varphi_{2})\cos(\varphi_{3})\\
&\,\,\vdots \\
x_{n-1}&=\sin(\varphi_{1})\cdots \sin(\varphi_{n-2})\cos(\varphi_{n-1})\\
x_{n}&=\sin(\varphi_{1})\cdots \sin(\varphi_{n-2})\sin(\varphi_{n-1})
\end{aligned}\right.
\end{equation}
其中$\varphi_{n−1}\in [0, 2\pi)$而剩下的$\varphi$范围是$[0, \pi]$。此时，$\boldsymbol{x}$和$\boldsymbol{y}$的夹角是：
\begin{equation}\arccos \langle \boldsymbol{x},\boldsymbol{y}\rangle = \arccos \cos(\varphi_{1}) = \varphi_{1}
\end{equation}
也就是说两者的夹角正好是$\varphi_1$。那么，$\boldsymbol{x}$和$\boldsymbol{y}$的夹角不超过$\theta$的概率是：
\begin{equation}P_n(\varphi_1\leq\theta) = \frac{n\text{维超球面上}\varphi_1\text{不超过}\theta\text{的积分}}{n\text{维超球面上的全积分}}
\end{equation}
而$n$维超球面上的积分微元是$\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}$（可在维基百科找到），所以
\begin{equation}\begin{aligned}
P_n(\varphi_1\leq\theta) =& \frac{\int_0^{2\pi}\cdots\int_0^{\pi}\int_0^{\theta}\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}}{\int_0^{2\pi}\cdots\int_0^{\pi}\int_0^{\pi}\sin^{n-2}(\varphi_{1})\sin^{n-3}(\varphi_{2})\cdots \sin(\varphi_{n-2})\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{n-1}}\\
=&\frac{(n-1)\text{维单位超球的表面积}\times\int_0^{\theta}\sin^{n-2}\varphi_{1} d\varphi_1}{n\text{维单位超球的表面积}}\\
=&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}} \int_0^{\theta}\sin^{n-2}\varphi_1 d\varphi_1
\end{aligned}
\end{equation}
这表明$\theta$的概率密度函数就是
\begin{equation}
p_n(\theta) = \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\sin^{n-2} \theta
\label{eq:theta}\end{equation}
有时候我们想关心$\eta=\cos\theta$的分布，这时候需要做一下概率密度的换元
\begin{equation}\begin{aligned}
p_n(\eta)=&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\sin^{n-2} (\arccos\eta)\left|\frac{d\theta}{d\eta}\right|\\
=&\frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}(1-\eta^2)^{(n-3)/2}\\
\end{aligned}\label{eq:cos}\end{equation}

分布情况 #

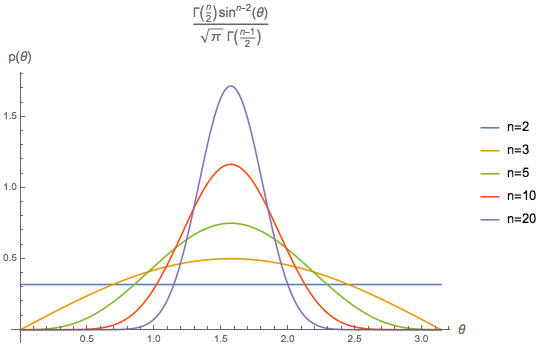
由$\eqref{eq:theta}$和$\eqref{eq:cos}$我们可以看到，当$n=2$时，夹角$\theta$的分布是一个均匀分布，而当$n=3$时，夹角余弦$\cos\theta$的分布是均匀分布。这两个结果说明在我们所能感知到的二维和三维空间中，角度的分布是比较均匀的。但是$n$比较大的时候呢？比如$n=20,50$？

从$p_n(\theta)\sim\sin^{n-2}\theta$的形式可以发现，当$n\geq 3$时，最大概率是$\theta=\frac{\pi}{2}$（即90度），另外$\sin^{n-2}\theta$也是关于$\theta=\frac{\pi}{2}$对称的，所以它的均值也是$\frac{\pi}{2}$。但这还不能充分描述分布情况，我们还需要考虑方差
\begin{equation}
Var_n(\theta) = \frac{\Gamma\left(\frac{n}{2}\right)}{\Gamma\left(\frac{n-1}{2}\right)\sqrt{\pi}}\int_0^{\pi}\left(\theta-\frac{\pi}{2}\right)^2\sin^{n-2} \theta d\theta\end{equation}
这个积分有解析解，但是形式很麻烦（喜欢看的话可以自己用Mathematica去算），我们来看部分数值解就好：
$$\begin{array}{c|c}
\hline
n & \text{方差}\\
\hline
3 & 0.467401\\
10 & 0.110661\\
20 & 0.0525832\\
50 & 0.0204053\\
100 & 0.0101007\\
200 & 0.00502508\\
1000 & 0.001001\\
\hline
\end{array}$$
可以看到，随着$n$的增大，方差越来越小，这意味着高维空间中任意两个向量的夹角几乎都集中在$\frac{\pi}{2}$附近，换言之，高维空间中任意两个向量几乎都是垂直的。

当然，从图像也可以看出：

p(θ)的图像

如果想要近似解析解的读者，可以考虑用拉普拉斯方法，用一个高斯分布去近似$p_n(\theta)$：在$\theta=\frac{\pi}{2}$处对$\ln \sin^{n-2}\theta$进行展开
\begin{equation}\ln \sin^{n-2}\theta=\frac{2-n}{2}\left(\theta - \frac{\pi}{2}\right)^2 + \mathcal{O}\left(\left(\theta - \frac{\pi}{2}\right)^4\right)\end{equation}
即
\begin{equation}\sin^{n-2}\theta\approx \exp\left[-\frac{n-2}{2}\left(\theta - \frac{\pi}{2}\right)^2\right]\end{equation}
从这个近似形式看，我们可以近似地认为$\theta$服从均值为$\frac{\pi}{2}$、方差为$\frac{1}{n-2}$的正态分布，即当$n$较大时，方差近似为$\frac{1}{n-2}$，这也能看出$n$越大，方差越小。

文章小结 #

本文对高维空间的夹角分布进行了推导，记录在此以备忘，同时也供有需要的读者参考。

转载到请包括本文地址：https://spaces.ac.cn/archives/7076

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。