2
Feb
喜迎新春！兔年快乐！2011~
By 苏剑林 | 2011-02-02 | 36791位读者 | 引用
28
May
科学空间：2011年6月重要天象
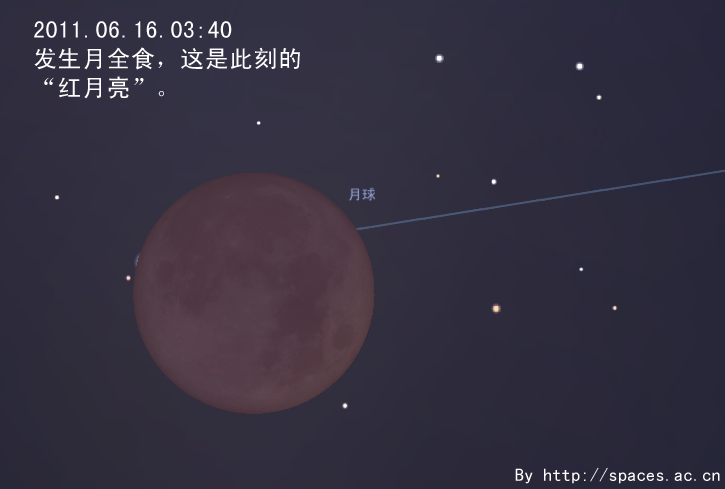
By 苏剑林 | 2011-05-28 | 26605位读者 | 引用
月全食-201106160340
6月中下旬，是北半球一年中黑夜最短的时期。今年6月22日是夏至节气，以北纬40°地区为例，当天天文昏影终到次日天文晨光始的间隔只有不到4小时50分钟。黑夜短暂会使我们可用于天文观测的时间缩短。但在夏至前后，午夜时分太阳也会在地平线下不太低的位置，这样我们就有可能整夜观测到一些类似国际空间站这样的低轨道人造天体。有兴趣的朋友可以查询相关的过境预报，挑战在一晚可以观测到多少次国际空间站过境这类的观测项目。发生在六月的日偏食和月全食，是今年天象的重头戏。接下来笔者就日偏食讲起，跟大家聊聊发生在6月的天象。
5
Mar
科学空间：2011年3月重要天象
By 苏剑林 | 2011-03-05 | 29964位读者 | 引用几颗经典行星，将成为3月星空剧场的主角。其中难得一见的水星将迎来一次观测条件很好的东大距，而到了下旬，土星也几乎整夜可见。随着落下时间的逐渐提前，木星的观测条件正逐渐变差。作为晨星的金星升起的时间也正不断推迟，我们将越来越难观测到它的身影。
天象大观
01日 11:40 金星合月: 1.7° S
11日 12:35 月合昴宿星团: 1.8° N
16日 04:16 水星合木星: 2° N
21日 07:21 春分
21日 19:00 月合角宿一: 2.5° N
21日 19:54 天王星合日
23日 08:59 水星大距: 18.6° E
31日 21:25 金星合月: 6.6° S
4
Apr
科学空间：2011年4月重要天象
By 苏剑林 | 2011-04-04 | 26805位读者 | 引用
28
May
遐思1：n次代数方程的解可以这样表示吗？
By 苏剑林 | 2011-05-28 | 29098位读者 | 引用打从科学空间建立起，就已经设立了“问题百科”这一个分类，但内容一直都很少，主要是平时太懒去总结一些问题。现在得要养成善于思考、总结的习惯了。
前几天到网上印刷了《天遇》和《无法解出的方程》来阅读，两者都是我很感兴趣的书。想当初在初中阶段阅读《数学史选讲》时，我最感兴趣的就是解方程方面的内容（根式解），通过研究理解了1到4次方程的求根公式，并通过阅读知道了4次以上的代数方程没有一般的根式可解。这在当时是多么值得高兴的一件事情！！
现在，稍稍阅读了《无法解出的方程》后，结合我之前在代数方程方面的一些总结，提出一个问题：
若任意的一元n次方程$\sum_{i=0}^{n} a_i x^i=0$的根记为$x_i=R_{n,i}(a_0,a_1,...,a_n)$
那么，是否存在大于3的n，使得任意的一元(n+1)次方程的根能够用加、减、乘、除、幂、开方以及$R_{j,i}$（j可以是1到n的任意整数）通过有限步骤运算出来？
这个问题可以换一个近似但不等价的说法：
若一元1次、2次、...、n次均可以根式解答，那么一元(n+1)次方程能否有根式解？
也就是说，(n+1)次方程的根能够表示成 1到n次方程的根与加、减、乘、除、幂、开方的有限次运算？
（不考虑前提的正确与否，显然n=4已经不成立了，当时n=5,6,7,8,...等有没有可能呢？）
期待有人能够解决^_^
19
Jun
向量结合复数：常曲率曲线(1)
By 苏剑林 | 2011-06-19 | 29590位读者 | 引用在之前的一篇向量系列的文章中，我们通过结合物理与向量来巧妙地推导出了曲线（包括平面和空间的）的曲率半径为
$$R=\frac{v^2}{a_c}=\frac{|\dot{\vec{r}}|^3}{|\dot{\vec{r}}\times \ddot{\vec{r}}|}\tag{1}$$
曲率则是曲率半径的导数：$\rho=\frac{1}{R}$。我们反过来思考一下：曲率恒定的平面曲线是否只有圆？
答案貌似是很显然的，我们需要证明一下。
由于只是考虑平面情况，我们先设$\dot{\vec{r}}=(v cos\theta,v sin\theta)=z=ve^{i\theta}$，代入(1)得到
$\frac{\dot{\theta}}{v}=\rho$————(2)
6
Jul
科学空间：2011年7月重要天象
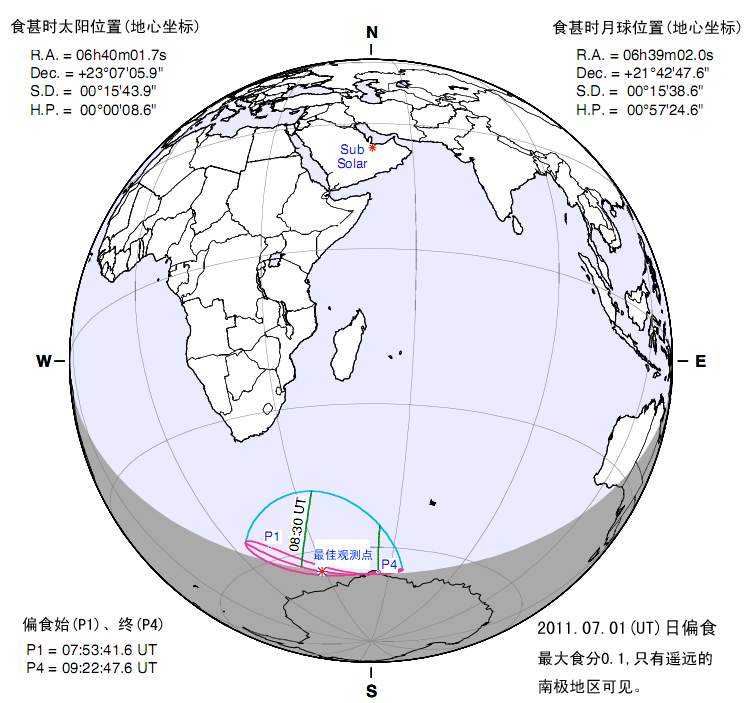
By 苏剑林 | 2011-07-06 | 22965位读者 | 引用
在农村，7月是忙碌的月份，农民们要忙着收割稻谷，收割完后要晒谷，同时还得准备“下秧”，准备新一轮的耕，BoJone家自然也不例外。不过我家田比较少（1亩左右），收割机几分钟搞定，谷也三两天就晒完了。不过在晒谷的时候，BoJone在考虑一个“收谷”问题：
晒谷时得先把成堆的谷子摊开，薄薄地平铺在平地上，等到傍晚或即将下雨时（这是最惨的情况，搞不好会淋谷）就将其收起来。问题就源于这里，一般来说我们会把谷均匀地铺成矩形，要把所有的谷都推到矩形里或外的哪一点上，才使得我们做功做小？
这个问题还可以推广开来，例如对于一地任意形状的谷子（如三角形），把它集中堆到哪个点最“轻松”？一堆固定质量的谷子，要把它平铺成什么形状，才使得收谷时最“轻松”？当然，这个问题的解不仅仅用于“收谷”，在很多规划建设中也可以应用到，例如要在一个人口大致均匀的城市中建设一个服务中心，这个服务中心应该建在哪里？这有点类似于我们之前讨论过的费马点问题 ，都是费马点只考虑了三个点的距离，而这个问题得考虑所有点的距离。
最近评论