基于GRU和AM-Softmax的句子相似度模型
By 苏剑林 | 2018-07-29 | 436095位读者 |搞计算机视觉的朋友会知道,AM-Softmax是人脸识别中的成果。所以这篇文章就是借鉴人脸识别的做法来做句子相似度模型,顺便介绍在Keras下各种margin loss的写法。
背景 #
细想之下会发现,句子相似度与人脸识别有很多的相似之处~
已有的做法 #
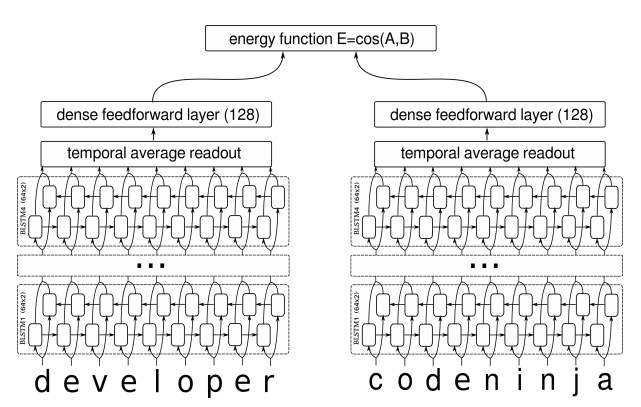
在我搜索到的资料中,深度学习做句子相似度模型,就只有两种做法:一是输入一对句子,然后输出一个0/1标签代表相似程度,也就是视为一个二分类问题,比如《Learning Text Similarity with Siamese Recurrent Networks》中的模型是这样的
包括今年拍拍贷的“魔镜杯”,也是这种格式。另外一种做法是输入一个三元组“(句子A,跟A相似的句子,跟A不相似的句子)”,然后用triplet loss的做法解决,比如文章《Applying Deep Learning To Answer Selection: A Study And An Open Task》中的做法。
这两种做法其实也可以看成是一种,本质上是一样的,只不过loss和训练方法有所差别。但是,这两种方法却都有一个很严重的问题:负样本采样严重不足,导致效果提升非常慢。
使用场景 #
我们不妨回顾一下我们使用句子相似度模型的场景。一般来说,我们事先存好了很多FAQ对,也就是“问题-答案”的语料对。当我们碰到一个新问题时,我们就需要比较这个新问题与原来数据库中所有问题的相似度,找出最相似的那个,根据相似度和阈值决定是否做出回答。
注意,这里边包含了两个要素,第一是“所有”,理论上来说,我们跟数据库中的所有问题都比较一次,然后找出最相似的;第二是“阈值”,我们也不知道新问题在数据库中是否有答案,因此这个阈值决定是我们是否要做出回应。如果不管三七二十一都取top1来作答,那体验也会很差的。
我们主要关心“所有”(事实上,“所有”解决了,“阈值”也就解决了)。“所有”意味着在训练的时候,对于每个句子,除了仅有的几个相似句是正样本,其它所有句子都应该作为负样本。但如果用前面的做法,其实我们很难完整地采样所有的负样本出来,而且就算可以做到,训练时间也非常长。这就是前面说的弊端所在。
来自人脸的帮助 #
我一直觉得,在机器学习领域中,其实不应该过分“划清界线”,比如有些读者觉得自己是做NLP的,于是就不碰图像,反过来做图像的,看到NLP的就远而避之。事实上,整个机器学习领域之间的沟壑并没有那么大,很多东西的本质都是一样的,只是场景不同而已。比如,所谓的句子相似度模型,其实几乎就完全对应于人脸识别任务,而人脸识别目前已经相当成熟了,显然我们是可以借鉴的。
先不说模型,我们来想象一下人脸识别的使用场景。比如公司内可以用人脸识别打卡,当有了一个人脸识别模型后,我们事先会存好一些公司员工的人脸照片,然后每天上班时,先拍一张员工的人脸照(实时拍摄,显然不会跟已经存好的照片完全吻合),然后要判断他/她是不是公司的员工,如果是,还要确定是哪一位员工。
试想一下,将上面的场景中,“人脸”换成“句子”,是不是就是句子相似度模型的使用场景呢?
显然,句子相似度模型可以是说NLP中的人脸识别了。
模型 #
句子相似度和人脸识别在各方面都很相似:从模型的使用到构建乃至数据集的量级上,都是如此地接近。所以,几乎人脸识别的一切模型和技巧,都可以用在句子相似度模型上。
作为分类问题 #
事实上,前面说的triplet loss,也是训练人脸识别模型的标准方法之一。triplet loss本身没有错,反而,如果能精调参数并且重新训练,它效果还可能非常好。只是在很多情况下,它实在是太低效了。当前,更标准的做法是:视为一个多分类问题。
比如,假设训练集里边有10万个不同的人,每个人5张人脸图,那么就有50万张训练图片了。然后我们训练一个CNN模型,对图片提取特征,并构建一个10万分类的模型。没错,就是跟mnist一样的分类问题,只不过这时候分类数目大得多,有多少个不同的人就有多少类。那么,句子相似度问题也可以这样做,可以将训练集划分为很多组“同义句”,然后有多少组就有多少类,也将句子相似度问题当作分类问题来做。
注意,这仅仅是训练,最后训练出来的分类模型可能毫无用处。这不难想象,我们可以用已有的人脸数据库来训练一个人脸识别模型,但我们的使用场景可能是公司打卡,也就是说要识别的人脸是公司内部的员工脸,他们显然不会在公开的人脸数据库中。所以分类模型是没有意义的,真正有意义的是分类之前的特征提取模型。比如,一个典型的CNN分类模型可以简写为两步
$$\begin{aligned}\boldsymbol{z} = CNN(\boldsymbol{x})\\
\boldsymbol{p}=\text{softmax}\big(\boldsymbol{z}\boldsymbol{W}\big)\end{aligned}\tag{1}$$
其中$\boldsymbol{x}$是输入,$\boldsymbol{p}$是每一类的概率输出,这里的softmax不用加偏置项。作为一个分类问题训练时,我们输出的是人脸图片$\boldsymbol{x}$和对应的one hot标签$\boldsymbol{p}$,但是在使用的时候,我们不用整个模型,我们只用$CNN(\boldsymbol{x})$这部分,这部分负责将每一张人脸图片转化为一个固定长度的向量。
有了这个转化模型(编码器,encoder),不管什么场景下,我们都可以对新人脸进行编码,然后转化为这些编码向量之间的比较,从而就不依赖原来的分类模型。所以,分类模型是一个训练方案,一旦训练完成,它就功成身退了,留下的是编码模型。
分类与排序 #
这样就可以了?还没有。前面说到,我们真正要做的是一个特征提取模型(编码器),并且用分类模型作为训练方案,而最后使用的方法是对特征提取模型的特征进行对比排序。
我们要做特征排序,但是借助分类模型训练,这两者等价吗?
答案是:相关但不等价。分类问题是怎么做的呢?直观来看,它是选定了一些类别中心,然后说
每个样本都属于距离它最近的中心的那一类。
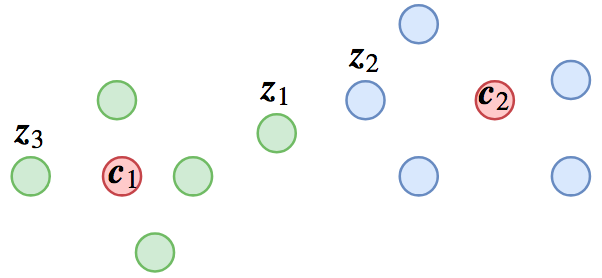
当然这些类别中心也是训练出来的,而这里的“距离”可以有多种可能性,比如欧式距离、cos值、内积都可以,一般的softmax对应的就是内积。分类问题的这种做法,就导致了下面的可能的分类结果:
这个分类结果有什么问题呢?我们留意图上的$\boldsymbol{z}_1,\boldsymbol{z}_2,\boldsymbol{z}_3$三个样本,其中$\boldsymbol{z}_1,\boldsymbol{z}_3$距离$\boldsymbol{c}_1$最近,所以它们是类别1的,$\boldsymbol{z}_2$距离$\boldsymbol{c}_2$最近,所以它是类别2的,假设这个分类没有错,也就是说$\boldsymbol{z}_1,\boldsymbol{z}_3$它们可能是同义句,$\boldsymbol{z}_2$跟它们不是同义的,又或者$\boldsymbol{z}_1,\boldsymbol{z}_3$是同一个人的人脸图,而$\boldsymbol{z}_2$则是另一个人的。
从分类角度,这结果很合理,但我们已经说过,我们最终不要分类模型,我们需要特征之间的比较。这样问题就很明显了:$\boldsymbol{z}_1,\boldsymbol{z}_2$距离这么近,却不是同一类的,$\boldsymbol{z}_1$跟$\boldsymbol{z}_3$距离这么远,却是同一类的。如果我们用特征排序的方法给$\boldsymbol{z}_1$找一个同义句,那么就会找到$\boldsymbol{z}_2$而不是$\boldsymbol{z}_3$,这就导致错误了。
loss #
上面说的,就是分类与排序的不等价性,也就是分类分对了,但是特征排序就会有误。当然,从图上也可以看出,尽管不完全等价,分类模型还是给了大部分的特征一个合理的位置分布,只是在边缘附近的特征,就可能出现问题。
margin softmax #
可以想象,问题出现在分类边界附近的那些点上面,而出现问题的原因,其实就是分类条件过于宽松,如果加强一下分类条件,就可以提升排序效果了,比如改为:
每个样本与它所属类的距离,必须小于它跟其他类的距离的1/2。
原来我们只需要小于它与其他类的距离,现在不但要这样,还要小于其它距离的一半,显然条件加强了,而前一个图所示的分类结果就不够好了,因为虽然如图有$\Vert \boldsymbol{z}_1 - \boldsymbol{c}_1\Vert < \Vert \boldsymbol{z}_1 - \boldsymbol{c}_2\Vert$,但是没有做到$\Vert \boldsymbol{z}_1 - \boldsymbol{c}_1\Vert < \frac{1}{2}\Vert \boldsymbol{z}_1 - \boldsymbol{c}_2\Vert$,所以还需要进一步优化loss。
假如按照这个条件训练完成后,我们可以想象,这时候$\boldsymbol{z}_1,\boldsymbol{z}_2$的距离就被拉大了,而$\boldsymbol{z}_1,\boldsymbol{z}_3$的距离就被缩小了,这正是我们所希望的结果:增大类间距离,缩小类内距离。
事实上,上面所说的方案,可以说就是人脸识别中很著名的方案l-softmax。人脸识别领域中,很多类似的loss被提出来,它们都是针对上述分类问题与排序问题的不等价性设计出来的,比如a-softmax、AM-Softmax、aAM-Softmax等,它们都统称margin softmax。而且,不仅有margin softmax,还有center loss,还有triplet loss的一些改进版本等等。
AM-Softmax #
我不是做图像的,因此人脸识别的故事我就讲不下去了,还是回到本文的正题。上面说到人脸识别不能用纯粹的softmax分类,必须要用margin softmax,而因为句子相似度模型和人脸识别模型的相似性,告诉我们句子相似度模型也是需要margin softmax的。总而言之,至少要挑一个margin softmax来实现呀。
其中,效果比较好而最容易实现的方案,当数AM-Softmax,本文就以它为例子来介绍这一类margin softmax的实现方案,最终实现一个句子相似度模型。
AM-Softmax的做法其实很简单,原来softmax是$\boldsymbol{p}=\text{softmax}\big(\boldsymbol{z}\boldsymbol{W}\big)$,设
$$\boldsymbol{W} = (\boldsymbol{c}_1,\boldsymbol{c}_2,\dots,\boldsymbol{c}_n)\tag{2}$$
那么softmax可以重新写为
$$\boldsymbol{p}=\text{softmax}\big(\langle\boldsymbol{z},\boldsymbol{c}_1\rangle, \langle\boldsymbol{z},\boldsymbol{c}_2\rangle, \dots, \langle\boldsymbol{z},\boldsymbol{c}_n\rangle\big)\tag{3}$$
然后loss取交叉熵,也就是
$$-\log p_t = - \log \frac{e^{\langle\boldsymbol{z},\boldsymbol{c}_t\rangle}}{\sum\limits_{i=1}^n e^{\langle\boldsymbol{z},\boldsymbol{c}_i\rangle}}\tag{4}$$
$t$为目标标签。而AM-Softmax做了两件事情:
1、将$\boldsymbol{z}$和$\boldsymbol{c}_i$都做l2归一化,也就是说,内积变成了cos值;
2、对目标cos值减去一个正数$m$,然后做比例缩放$s$。
即loss变为
$$-\log p_t = - \log \frac{e^{s\cdot(\cos\theta_t -m)}}{e^{s\cdot (\cos\theta_t -m)}+\sum\limits_{i\neq t} e^{s\cdot\cos\theta_i }}\tag{5}$$
其中$\theta_i$代表$\boldsymbol{z},\boldsymbol{c}_i$的夹角。在AM-Softmax原论文中,所使用的是$s=30,m=0.35$。
从AM-Softmax中,我们可以看到针对前面所提的问题的解决方案了。首先,$s$的存在是必要的,因为cos的范围是$[-1, 1]$,需要做好比例缩放,才允许$p_t$能足够接近于1(有必要的话)。当然,$s$并不改变相对大小,因此这不是核心改变,核心是原来应该是$\cos\theta_t $的地方,换成了$\cos\theta_t -m$。
随心所欲地margin #
前面提到,从分类问题到特征排序的不完全等价性,可以通过加强分类条件来解决,所谓加强,其实意思很简单,就是用一个新的函数$\psi(\theta_t) $来代替$\cos\theta_t $,只要
$$\psi(\theta_t) < \cos\theta_t\tag{6}$$
我们都可以认为是一种加强,而AM-Softmax则是取$\psi(\theta_t) =\cos\theta_t -m$,这估计是满足上式的最简单粗暴的方案了(幸好,它效果也很好)。
理解了这种思想之后,其实我们可以构造各种各样的$\psi(\theta_t)$了,毕竟理论上满足$(6)$式的都可以选取。前面我们也提到了l-softmax和a-softmax,它们相当于选择了$\psi(\theta_t)=\cos m\theta_t$,其中$m$是一个整数。但我们知道,$\cos m\theta_t < \cos \theta_t$并非总是成立的,所以论文中基于$\cos m\theta_t$构造了一个分段函数出来,显得特别麻烦,而且也使得模型极难收敛。事实上,我试验过下面的方式
$$\psi(\theta_t) = \min(\cos m\theta_t, \cos\theta_t)\tag{7}$$
结果媲美AM-Softmax(在句子相似度任务上)。所以,上述可以作为l-softmax和a-softmax的一个简单的替代品了吧,我称为simpler-a-softmax,有兴趣的读者可以试试在人脸上的效果。
实现 #
最后介绍本文对这些loss在Keras下的实现。测试环境的Python版本为2.7,Keras版本为2.1.5,tensorflow后端。
基本实现 #
用最基本的方式实现AM-Softmax并不困难,比如
from keras.models import Model
from keras.layers import *
import keras.backend as K
from keras.constraints import unit_norm
x_in = Input(shape=(maxlen,))
x_embedded = Embedding(len(chars)+2,
word_size)(x_in)
x = CuDNNGRU(word_size)(x_embedded)
x = Lambda(lambda x: K.l2_normalize(x, 1))(x)
pred = Dense(num_train,
use_bias=False,
kernel_constraint=unit_norm())(x)
encoder = Model(x_in, x) # 最终的目的是要得到一个编码器
model = Model(x_in, pred) # 用分类问题做训练
def amsoftmax_loss(y_true, y_pred, scale=30, margin=0.35):
y_pred = y_true * (y_pred - margin) + (1 - y_true) * y_pred
y_pred *= scale
return K.categorical_crossentropy(y_true, y_pred, from_logits=True)
model.compile(loss=amsoftmax_loss,
optimizer='adam',
metrics=['accuracy'])
Sparse版实现 #
上面的代码并不难理解,主要基于y_true是目标的one hot输入,这样一来,可以通过普通的乘法来取出目标的cos值,减去margin后再补回其他部分。
如果仅仅是玩个mnist这样的10分类,那么上述代码完全足够了。但在人脸识别或句子相似度场景,我们面对的事实上是数万分类甚至数十万的分类,这种情况下如果还是用one hot输入,就显得非常消耗内存了(主要是准备数据时也麻烦一些)。理想情况下,我们希望y_true只要输入对应分类的整数id。对于普通的交叉熵,Keras也提供了sparse_categorical_crossentropy的方案,便是应对这种需求,那么AM-Softmax能不能写个Sparse版出来呢?
一种比较简单的写法是,将转换one hot的过程写入到loss中,比如:
def sparse_amsoftmax_loss(y_true, y_pred, scale=30, margin=0.35):
y_true = K.cast(y_true[:, 0], 'int32') # 保证y_true的shape=(None,), dtype=int32
y_true = K.one_hot(y_true, K.int_shape(y_pred)[-1]) # 转换为one hot
y_pred = y_true * (y_pred - margin) + (1 - y_true) * y_pred
y_pred *= scale
return K.categorical_crossentropy(y_true, y_pred, from_logits=True)
这样确实能达成目的,但只不过对问题进行了转嫁,并没有真正跳过转one hot。我们可以用tensorflow的gather_nd函数,来实现真正地跳过转one hot的过程,下面是参考的代码
def sparse_amsoftmax_loss(y_true, y_pred, scale=30, margin=0.35):
y_true = K.expand_dims(y_true[:, 0], 1) # 保证y_true的shape=(None, 1)
y_true = K.cast(y_true, 'int32') # 保证y_true的dtype=int32
batch_idxs = K.arange(0, K.shape(y_true)[0])
batch_idxs = K.expand_dims(batch_idxs, 1)
idxs = K.concatenate([batch_idxs, y_true], 1)
y_true_pred = K.tf.gather_nd(y_pred, idxs) # 目标特征,用tf.gather_nd提取出来
y_true_pred = K.expand_dims(y_true_pred, 1)
y_true_pred_margin = y_true_pred - margin # 减去margin
_Z = K.concatenate([y_pred, y_true_pred_margin], 1) # 为计算配分函数
_Z = _Z * scale # 缩放结果,主要因为pred是cos值,范围[-1, 1]
logZ = K.logsumexp(_Z, 1, keepdims=True) # 用logsumexp,保证梯度不消失
logZ = logZ + K.log(1 - K.exp(scale * y_true_pred - logZ)) # 从Z中减去exp(scale * y_true_pred)
return - y_true_pred_margin * scale + logZ
这个代码会比前一个带one hot的代码要略微快一些。实现的关键是用tf.gather_nd把目标列提取出来,然后用logsumexp计算对数配分函数,这估计是实现交叉熵的标准方法了。基于此,可以修改为其它形式的margin softmax loss。现在就可以像sparse_categorical_crossentropy一样只输入类别id了,其它框架也可以参照着实现。
效果预览 #
一个完整的句子相似度模型可以在这里浏览:
https://github.com/bojone/margin-softmax/blob/master/sent_sim.py
这是一个基于字的模型,用GRU做编码器,所用到的语料tongyiju.csv如图(语料不共享,需要运行的读者请自行按照格式准备语料):
其中前面的id表示句子组别,用\t隔开,同一组的句子可以认为都是同一句,不同组的句子则是非同义句。
训练结果:训练集的分类问题上,能达到90%+的准确率,而验证集(evaluate函数)上,几种loss的top1、top5、top10的准确率分别为(没有精细调参)
$$\begin{array}{c|c|c|c}
\hline
& \text{top1 acc} & \text{top5 acc} & \text{top10 acc}\\
\hline
\text{softmax} & 0.9077 & 0.9565 & 0.9673\\
\text{AM-Softmax} & 0.9172 & 0.9607 & 0.9709\\
\text{simpler-asoftmax} & 0.9135 & 0.9587 & 0.9697 \\
\hline
\end{array}$$
值得一提的是,evaluate函数完全是按照真实的使用环境测试的,也就是说,验证集的每一个句子都没有出现过在训练集中,运行evaluate函数时,仅仅是在验证集内部进行排序,如果按相似度排序后的前$n$个句子中出现了输入句子的同义句,那么topn的命中数就加1。
因此,这样看来,准确率是很可观的,能满足工程使用了。下面是随便挑几个匹配的例子:
$$\begin{array}{c|c}
\hline
\text{源句子} & \text{广州的客运站的数目}\\
\hline
\text{相似排序} & \begin{array}{c|c}\text{相似句} & \text{相似度}\\
\hline
\text{广州有多少个客运站?} & 0.8281\\
\text{广州有几个汽车客运站} & 0.7980 \\
\text{广州天河有几个客运站} & 0.6781\\
\text{广州天河区有几个汽车客运站?} & 0.6527\\
\end{array}\\
\hline
\end{array}$$
$$\begin{array}{c|c}
\hline
\text{源句子} & \text{沙发一般有多高}\\
\hline
\text{相似排序} & \begin{array}{c|c}\text{相似句} & \text{相似度}\\
\hline
\text{沙发一般高度是多少} & 0.8658\\
\text{客厅沙发一般多高} & 0.7458 \\
\text{一般沙发普通高度是多少} & 0.7173\\
\text{沙发高度尺寸一般是多少} & 0.6872\\
\end{array}\\
\hline
\end{array}$$
$$\begin{array}{c|c}
\hline
\text{源句子} & \text{ps格式可以转换成ai格式吗}\\
\hline
\text{相似排序} & \begin{array}{c|c}\text{相似句} & \text{相似度}\\
\hline
\text{ps格式的图怎么转换成ai格式的图?} & 0.9351\\
\text{photoshop文件转成什么格式可以ai里面打开} & 0.6825 \\
\text{ps文件可以改成ai格式文件} & 0.6531\\
\text{视频格式转换的转换模式} & 0.5880\\
\end{array}\\
\hline
\end{array}$$
结论 #
本文阐述了笔者对句子相似度模型的理解,认为它的最佳做法并非二分类,也并非triplet loss,而是模仿人脸识别中的margin loss来做,这是能最快速提升效果的方案。当然,我并没有充分比较各种方法,仅仅是从我自己对人脸识别的粗浅了解中觉得应该是那样。欢迎读者测试并一同讨论。
转载到请包括本文地址:https://spaces.ac.cn/archives/5743
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 29, 2018). 《基于GRU和AM-Softmax的句子相似度模型 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5743
@online{kexuefm-5743,
title={基于GRU和AM-Softmax的句子相似度模型},
author={苏剑林},
year={2018},
month={Jul},
url={\url{https://spaces.ac.cn/archives/5743}},
}











March 18th, 2020
您好,读了您的文章后,我自己也开始进行了尝试,本人有一批文本数据,数据形式与文章中一致:数据中有大量group,每个group里有若干语义相同的句子。但是在实际训练中发现效果不佳,我怀疑是数据的问题,因为我的数据量比较大,大概有10W个group,即10W类别,每个类别约有3-5个句子,我在想是不是类别过多,而每类的数据过少导致的?不知道苏神怎么看这个问题?
我原来的数据也有10w个group。此外,基于am-softmax做句向量和检索的模型,我司现在也在用,已经用在工程了,所以思路和方法都不会有问题的。
感谢回复,每个group大概有多少个句子,也是3到5个吗?
一般不超过10个,多数5~10个。
好滴,感谢,我再试试
您好,有个问题想请教下。我在https://github.com/ZhuiyiTechnology/pretrained-models 这里发现了一个SimBERT的模型,这里提到使用UniLM+度量学习得到了和你这边一样的性能。这个SimBERT里使用的度量学习损失函数就是你文中所说的pair对吗,0/1标签,作为分类问题吗?
此外,感觉如果这么做,负例直接选取是否太过简单了,如果选取1个正例、k个负例,计算k+1个值的交叉熵是否合适呢?
“UniLM+度量学习”是另一种方式,确实是选择$k$个负例的,过几天会专门写个文章介绍一下训练方式。
好滴,坐等更新啊,学习一波!
March 24th, 2020
我用am-softmax接上Bert 做同义句多分类(29000),但是就算学习率设很小还是sparse_categorical_crossentropy: nan这样,梯度爆炸了.怎么办?数据没问题
解决了,打扰。
能分享一下你的解决办法吗?非常感谢~
March 30th, 2020
你好,如果我采用few-shot的方式,每次采样一个类中的部分数据,这样公式的分母就少了几项,类别中心就有了偏差,请问有什么方法解决吗?
深度学习的训练,本身就是批采样的呀,难道你还能全量梯度下降么?
明白了,感谢苏神!
April 26th, 2020
[...]为了复现该大神https://kexue.fm/archives/5743的所需要的数据集。[...]
August 24th, 2020
请教分类数据极度不均衡的情况如何处理,有什么建议不?我的场景是大约10w个分类,90%的分类样本数在1-5个内,5%的分类样本数在100-500个。我看到人脸识别的一些做法是删除样本数少于30的类别。说样本数太少的类别无法形成聚类中心。谢谢!
如果你最终的目标是为了学习特征然后去相似度排序,那么可以考虑想办法让每一类均衡化(删除部分过多或者过少的样本)。
November 17th, 2020
y_pred = y_true * (y_pred - margin) + (1 - y_true) * y_pred与直接y_pred - y_true * margin有何区别?
没什么区别。
April 18th, 2021
您好。我用你的方法在我的模型上进行尝试,(模型中用的是Bert和LSTM), 发现sparse_categorical_accuracy一直在一个非常低的值。而且我训练过程特别慢(相当于之前的0/1分类法),一个epoch要运行很久,之前一个epoch运行两个多小时,现在一天多了,还没跑完。希望得到指点,十分感谢~
你觉得就这些信息,我能指点什么呢?全体同义句组作为分类数来做am-softmax,对性能要求确实很高的了,这个没办法。
April 19th, 2021
谢谢你的回复。很抱歉,的确是信息不够。我的改动和我之前的版本主要就是最后的三个dense层变成了 dense(90000):
output1 = tf.keras.layers.Dense(512*2, activation="relu")(dropout)
output2 = tf.keras.layers.Dense(512, activation="softmax")(output1)
output = tf.keras.layers.Dense(1, activation="sigmoid")(output2)
=》
output = tf.keras.layers.Dense(90000, use_bias=False, kernel_constraint=unit_norm())(dropout)
这个改动导致Trainable params: 7,870,465 变成了Trainable params: 179,191,808,应该就是导致一个epoch运行时间从之前的两个半小时变成两天还没有运行完的原因?我用的机器是实验室性能非常好的机器了。但这样的话运行一次就要几十天了,肯定是没法用的。
另外一个改动是loss function 从binary_crossentropy变成了sparse_amsoftmax_loss。
accuracy 也从70%变成了非常低的值,是不是可能训练不够?
我不知道面对这种情况,有没有什么优化的空间?或者我有什么地方没有考虑到或者做错了。非常非常感谢你的指点,让我可以尝试一下?
如果你原来需要两个半小时,那么现在可能是需要翻几倍,但是两天没跑完我确实觉得有点意外,因为90000分类虽然看起来大,但也不算特别大。第一个可以做的尝试是,最后分类的特征维度降低一些(从512降到128或64试试)。
最后我确认一下,你是用cpu跑的还是gpu跑的?
好的,你是说在DENSE(90000)前将输入层(dropout层)的维度降低,对吧? 我试一下,非常感谢。
另外,我用GPU跑的。
谢谢指点,运行长的问题解决了。我把前面几层的维度都降低了,参数再次回到百万级。
现在等运行完epoch再看看accuracy的问题。再次感谢~
好的。
September 18th, 2021
看完之后,有点疑问:得到encoder之后,可以将FAQ库中的问题全部转换成句向量a1,a2-an,然后将query转换成句向量q,那么如何计算q和a之间的相似度呢?
自己写函数计算余弦值...或者用faiss之类的库。