Tiger:一个“抠”到极致的优化器
By 苏剑林 | 2023-03-07 | 44920位读者 | 引用这段时间笔者一直在实验《Google新搜出的优化器Lion:效率与效果兼得的“训练狮”》所介绍的Lion优化器。之所以对Lion饶有兴致,是因为它跟笔者之前的关于理想优化器的一些想法不谋而合,但当时笔者没有调出好的效果,而Lion则做好了。
相比标准的Lion,笔者更感兴趣的是它在$\beta_1=\beta_2$时的特殊例子,这里称之为“Tiger”。Tiger只用到了动量来构建更新量,根据《隐藏在动量中的梯度累积:少更新几步,效果反而更好?》的结论,此时我们不新增一组参数来“无感”地实现梯度累积!这也意味着在我们有梯度累积需求时,Tiger已经达到了显存占用的最优解,这也是“Tiger”这个名字的来源(Tight-fisted Optimizer,抠门的优化器,不舍得多花一点显存)。
此外,Tiger还加入了我们的一些超参数调节经验,以及提出了一个防止模型出现NaN(尤其是混合精度训练下)的简单策略。我们的初步实验显示,Tiger的这些改动,能够更加友好地完成模型(尤其是大模型)的训练。
Lion/Tiger优化器训练下的Embedding异常和对策
By 苏剑林 | 2023-08-28 | 30364位读者 | 引用打从在《Tiger:一个“抠”到极致的优化器》提出了Tiger优化器之后,Tiger就一直成为了我训练模型的“标配”优化器。最近笔者已经尝试将Tiger用到了70亿参数模型的预训练之中,前期效果看上来尚可,初步说明Tiger也是能Scale Up的。不过,在查看训练好的模型权重时,笔者发现Embedding出现了一些异常值,有些Embedding的分量达到了$\pm 100$的级别。
经过分析,笔者发现类似现象并不会在Adam中出现,这是Tiger或者Lion这种带符号函数$\text{sign}$的优化器特有的问题,对此文末提供了两种参考解决方案。本文将记录笔者的分析过程,供大家参考。
现象
接下来,我们的分析都以Tiger优化器为例,但分析过程和结论同样适用于Lion。
从Hessian近似看自适应学习率优化器
By 苏剑林 | 2024-11-29 | 9708位读者 | 引用这几天在重温去年的Meta的一篇论文《A Theory on Adam Instability in Large-Scale Machine Learning》,里边给出了看待Adam等自适应学习率优化器的新视角:它指出梯度平方的滑动平均某种程度上近似于在估计Hessian矩阵的平方,从而Adam、RMSprop等优化器实际上近似于二阶的Newton法。
这个角度颇为新颖,而且表面上跟以往的一些Hessian近似有明显的差异,因此值得我们去学习和思考一番。
牛顿下降
设损失函数为$\mathcal{L}(\boldsymbol{\theta})$,其中待优化参数为$\boldsymbol{\theta}$,我们的优化目标是
\begin{equation}\boldsymbol{\theta}^* = \mathop{\text{argmin}}_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\label{eq:loss}\end{equation}
假设$\boldsymbol{\theta}$的当前值是$\boldsymbol{\theta}_t$,Newton法通过将损失函数展开到二阶来寻求$\boldsymbol{\theta}_{t+1}$:
\begin{equation}\mathcal{L}(\boldsymbol{\theta})\approx \mathcal{L}(\boldsymbol{\theta}_t) + \boldsymbol{g}_t^{\top}(\boldsymbol{\theta} - \boldsymbol{\theta}_t) + \frac{1}{2}(\boldsymbol{\theta} - \boldsymbol{\theta}_t)^{\top}\boldsymbol{\mathcal{H}}_t(\boldsymbol{\theta} - \boldsymbol{\theta}_t)\end{equation}
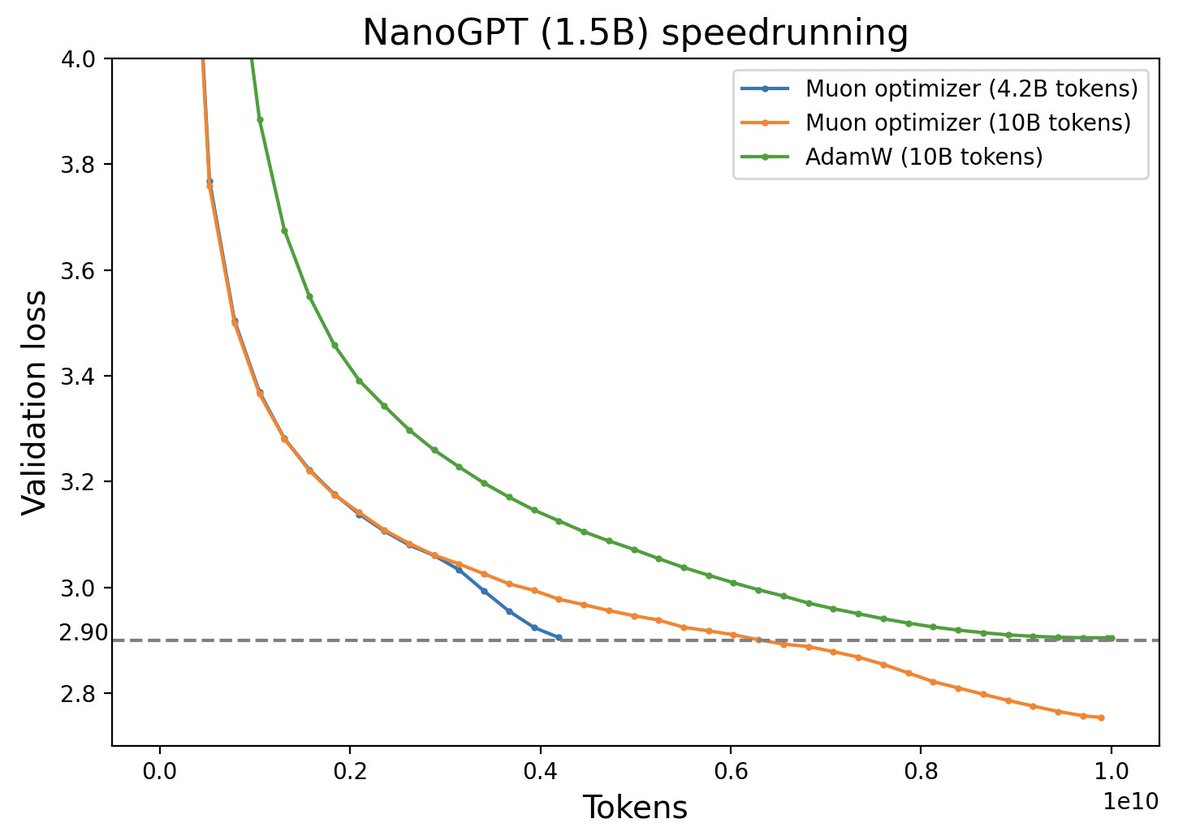
Muon优化器赏析:从向量到矩阵的本质跨越
By 苏剑林 | 2024-12-10 | 8225位读者 | 引用随着LLM时代的到来,学术界对于优化器的研究热情似乎有所减退。这主要是因为目前主流的AdamW已经能够满足大多数需求,而如果对优化器“大动干戈”,那么需要巨大的验证成本。因此,当前优化器的变化,多数都只是工业界根据自己的训练经验来对AdamW打的一些小补丁。
不过,最近推特上一个名为“Muon”的优化器颇为热闹,它声称比AdamW更为高效,且并不只是在Adam基础上的“小打小闹”,而是体现了关于向量与矩阵差异的一些值得深思的原理。本文让我们一起赏析一番。
Adam的epsilon如何影响学习率的Scaling Law?
By 苏剑林 | 2024-11-18 | 13461位读者 | 引用上一篇文章《当Batch Size增大时,学习率该如何随之变化?》我们从多个角度讨论了学习率与Batch Size之间的缩放规律,其中对于Adam优化器我们采用了SignSGD近似,这是分析Adam优化器常用的手段。那么一个很自然的问题就是:用SignSGD来近似Adam究竟有多科学呢?
我们知道,Adam优化器的更新量分母会带有一个$\epsilon$,初衷是预防除零错误,所以其值通常很接近于零,以至于我们做理论分析的时候通常选择忽略掉它。然而,当前LLM的训练尤其是低精度训练,我们往往会选择偏大的$\epsilon$,这导致在训练的中、后期$\epsilon$往往已经超过梯度平方大小,所以$\epsilon$的存在事实上已经不可忽略。
因此,这篇文章我们试图探索$\epsilon$如何影响Adam的学习率与Batch Size的Scaling Law,为相关问题提供一个参考的计算方案。
从动力学角度看优化算法(四):GAN的第三个阶段
By 苏剑林 | 2019-05-03 | 97612位读者 | 引用在对GAN的学习和思考过程中,我发现我不仅学习到了一种有效的生成模型,而且它全面地促进了我对各种模型各方面的理解,比如模型的优化和理解视角、正则项的意义、损失函数与概率分布的联系、概率推断等等。GAN不单单是一个“造假的玩具”,而是具有深刻意义的概率模型和推断方法。
作为事后的总结,我觉得对GAN的理解可以粗糙地分为三个阶段:
1、样本阶段:在这个阶段中,我们了解了GAN的“鉴别者-造假者”诠释,懂得从这个原理出发来写出基本的GAN公式(如原始GAN、LSGAN),比如判别器和生成器的loss,并且完成简单GAN的训练;同时,我们知道GAN有能力让图片更“真”,利用这个特性可以把GAN嵌入到一些综合模型中。
2、分布阶段:在这个阶段中,我们会从概率分布及其散度的视角来分析GAN,典型的例子是WGAN和f-GAN,同时能基本理解GAN的训练困难问题,比如梯度消失和mode collapse等,甚至能基本地了解变分推断,懂得自己写出一些概率散度,继而构造一些新的GAN形式。
3、动力学阶段:在这个阶段中,我们开始结合优化器来分析GAN的收敛过程,试图了解GAN是否能真的达到理论的均衡点,进而理解GAN的loss和正则项等因素如何影响的收敛过程,由此可以针对性地提出一些训练策略,引导GAN模型到达理论均衡点,从而提高GAN的效果。
基于fine tune的图像分类(百度分狗竞赛)
By 苏剑林 | 2017-10-13 | 28923位读者 | 引用前两年百度的大数据竞赛都是自然语言处理方面的,今年画风一转,变成了图像的细颗粒度分类,赛题内容就是将宠物狗归为100类中的其中一类。这个任务本身是很平凡的,做法也很常规,无外乎就是数据扩增、imagenet模型的fine tune、模型集成三个方面。笔者并不擅长于模型集成,只做了前面两个步骤,成绩也非常一般(准确率80%上下)。但感觉里边的某些代码可能对读者有帮助,遂共享一翻。下面结合着代码来讲解。
比赛官网(随时有失效的可能):http://js.baidu.com
模型
模型主要用tensorflow+keras实现。首先自然是导入各种模块
#! -*- coding:utf-8 -*-
import numpy as np
from scipy import misc
import tensorflow as tf
from keras.applications.xception import Xception,preprocess_input
from keras.layers import Input,Dense,Lambda,Embedding
from keras.layers.merge import multiply
from keras import backend as K
from keras.models import Model
from keras.optimizers import SGD
from tqdm import tqdm
import glob
np.random.seed(2017)
tf.set_random_seed(2017)
基于Conv1D的光谱分类模型(一维序列分类)
By 苏剑林 | 2018-05-02 | 119397位读者 | 引用前段时间天池出了个天文数据挖掘竞赛——LAMOST光谱分类(将对应的光谱识别为4类中的一类),虽然没有奖金,但还是觉得挺有意思,所以就报名参加了。做了一段时间,成绩自我感觉还可以,然而最后我却忘记了(或者说根本就没留意到)初赛最后两天还有一步是提交新的测试集结果,然后就没有然后了,留下了一个未竟的模型,可谓“出师未捷身先死”,还是被自己弄死的~
后来跟其他参赛选手讨论了一下,发现其实我的这个模型还是不错的。当时我记得初赛第一名的成绩是0.83+,而我当时的成绩是0.82+,排名大概是第4、5左右,而且据说很多分数在0.8+的队伍都已经使用了融合模型,而我这0.82+的成绩仅仅是单模型的结果~在平时的群聊中发现也有不少朋友在做一维序列分类模型,而光谱分类本质上也就是一个一维的序列分类,所以分享一下模型,估计对相关朋友会有一定的参考价值。
模型
事实上也不是什么特别的模型,就是普通的一维卷积加残差,对于熟悉图像处理的朋友,这实在是再普通不过的结构了。









最近评论