31
Jul
关于无理数及其和的证明
By 苏剑林 | 2009-07-31 | 25444位读者 | 引用 在中学,有理数的定义为整数和分数的集合,统一来说就是能够写成两个整数之比的数。那相对地,无理数自然就是不能写成两个整数之比的数了,也就是无限不循环小数,比如π,√2等等。历史上无理数的发现带来了第一次数学危机,并生下了一颗“金蛋”,不过发现者却因此丢掉了生命。让我们永远铭记——希帕索斯(Hippasus)。
在中学,有理数的定义为整数和分数的集合,统一来说就是能够写成两个整数之比的数。那相对地,无理数自然就是不能写成两个整数之比的数了,也就是无限不循环小数,比如π,√2等等。历史上无理数的发现带来了第一次数学危机,并生下了一颗“金蛋”,不过发现者却因此丢掉了生命。让我们永远铭记——希帕索斯(Hippasus)。
历史:
http://baike.baidu.com/view/1167.htm#2
在这里对无理数就不多说些什么了,主要是谈谈相关的证明而已。
先说明,以下是我自己的证明方法,当然我相信有一种方法是通用的,但是我没有找出来。
31
Jul
【NASA每日一图】木星的新疤痕
By 苏剑林 | 2009-07-31 | 18004位读者 | 引用椭圆面积和周长的求法,看上去没有什么区别。不过实际上它们的难度有着天壤之别。
椭圆所包围的面积是S=πab,这里的a和b是半长轴和半短轴。仅根据椭圆标准方程就可以推导出来。
目前还没有找到椭圆周长的一般公式,要想精确求解,只有代入以下无穷级数:
C=2πa[1−(1/2)2(ca)2−(1⋅3/2⋅4)2c4/3a4−(1⋅3⋅5/2⋅4⋅6)2c6/5a6−...]
可以写成:
C=2πa∞∑n=0−[n∏m=1(2m−1/2m)]2c2n/a2n(2n−1)
距离c 叫做椭圆的线性离心率,等于从中心到任一焦点的距离
1
Aug
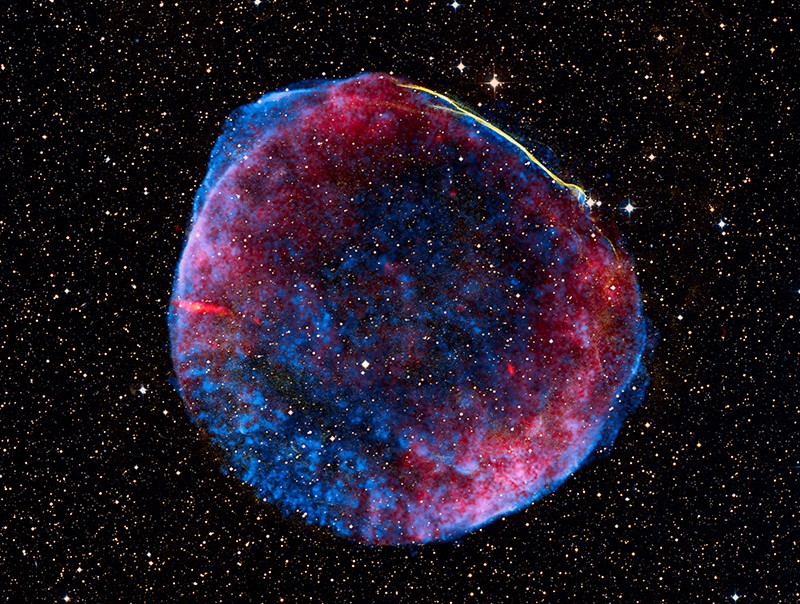
【NASA每日一图】明亮的超新星爆发
By 苏剑林 | 2009-08-01 | 19632位读者 | 引用
2
Aug
一道级数求和证明题(非数学归纳法)
By 苏剑林 | 2009-08-02 | 19351位读者 | 引用
2
Aug
【NASA每日一图】NGC 6559 的恒星,尘埃和星云
By 苏剑林 | 2009-08-02 | 27860位读者 | 引用
3
Aug
【NASA每日一图】正在形成的恒星
By 苏剑林 | 2009-08-03 | 19038位读者 | 引用
4
Aug












最近评论