1
Feb
新春快乐！2011年2月重要天象
By 苏剑林 | 2011-02-01 | 29797位读者 | 引用相对于其他月份，2月的天空总显得有些寂寞。不过，这并不影响我们开心的情绪。因为通常中国最重要的节日——春节都发生在二月，今年也不例外。春节是农历年的开始，对中国人来说，它才是真正的2011的第一天！新年伊始，科学空间大家天天快乐，心想事成，愿BoJone的人生之旅上能够一直与各位科学爱好者相伴。
天象大观：
01日 金星距太阳: 45.4° W
05日 00:49 火星合日
08日 半人马α流星雨极大
12日 05:32 月合昴宿星团: 1.5° N
17日 17:15 海王星合日
22日 09:02 月合角宿一: 2.8° N
25日 13:26 月合心宿二: 2.9° S
25日 16:27 水星上合日.
3
Feb
[SETI-50周年]茫茫宇宙觅知音
By 苏剑林 | 2011-02-03 | 19632位读者 | 引用转载自2011年1月的《天文爱好者》 作者：薛国轩
“多萝西计划”再探地外文明
据美国空间网站2010年11月13日报道，在人类“探索地外文明”（英文缩写为SETI）50周年纪念之际，世界多个国家的天文学家从本月起再度展开“且听外星人”的联合行动，以延续开始于1960年的“奥兹玛计划”。新的探索活动被命名为“多萝西计划”（Project Dorothy），已于11月5日正式启动，将持续整整一个月时间，来自澳大利亚、日本、韩国、意大利、荷兰、法国、阿根廷和美国的天文学家参与其中。他们将把大大小小的望远镜指向地球周围的一些星球，以期收听到外星人的“天外来音”。
Allen Telescope Array
6
Feb
[SETI-50周年]送给外星人的礼物
By 苏剑林 | 2011-02-06 | 34692位读者 | 引用转载自2011年1月的《天文爱好者》 作者：钟晚晴
生命出现是天体演化的必然结果
探索地外文明
15世纪时，欧洲的文艺复兴运动引起了人们宇宙观的大革命。哥白尼学说的主要传播者之一，意大利思想家布魯诺毫不含糊地宣扬日心说并且提及“外星人”是否存在问题，他这样写到：“宇宙中存在着无数的太阳，存在着无数绕自己太阳运转的地球，就像我们的七个行星绕着我们的太陌运转似的……。在这些世界上居住着各种生物。”科学大师伽利略率先把望远镜指向星空，继而几百年以来有了一系列天文发现。太空视野的大幵阔常引发人类这样的追问：除了地球之外，茫茫宇宙中还存在别的文明星球吗？如果存在，能否找到人类的知音一智慧生命？
科学家通过研究地球化石发现，早在35亿年前地球上就已有了一种发育得比较高级的单细胞生物，即蓝藻类;根据恒星演化理论以及对地球上古老岩石和陨星物质分析知道，太阳和地球的形成比这种生物的出现至少还要早约十几亿年左右。太阳系自原始星云形成后大约经过50亿年地球上才有人类。此外，科学考察表明，在最近五亿年来（根据化石考查）已经有过五次生命大灭绝，人类是五亿年来最后一次灭绝以后从猿进化而来。天体的环境变化往往决定着许许多多生命的命运，例如6500万年前恐龙的绝灭，据说就是遭遇了寒冷的冰期或地球被一颗直径十几千米的小天体撞击的结果。
从20世纪初以来，天文学的研究成果是显著的，例如关于银河系的许多发现，河外星系及宇宙膨胀的发现，特别是后来发现类星体、星际分子、脉冲星、河外星系超新星爆发等等。在进入空间科学和电子计算机科学时代以来，人们对宇宙天体的研究更加深入，每年都有许多新的天体被发现、探究。
4
Feb
《方程与宇宙》:限制性三体的那些事儿(八)
By 苏剑林 | 2011-02-04 | 26619位读者 | 引用在上一些关于限制性三体问题的探讨中，我们得出了在平面上的方程：
$$\ddot{R}+2i\omega \dot{R}=\omega^2 R-GM\frac{R-l_1}{|R-l_1|^3}-Gm\frac{R-l_2}{|R-l_2|^3}\tag{32}$$
能量积分为：
$$\frac{1}{2}|\dot{R}|^2=\frac{1}{2} \omega^2 |R|^2+\frac{GM}{|R-l_1|}+\frac{Gm}{|R-l_2|}-C\tag{33}$$
下面就以这两个方程为基础，再说说限制性三体问题的那些事儿...
28
May
科学空间：2011年6月重要天象
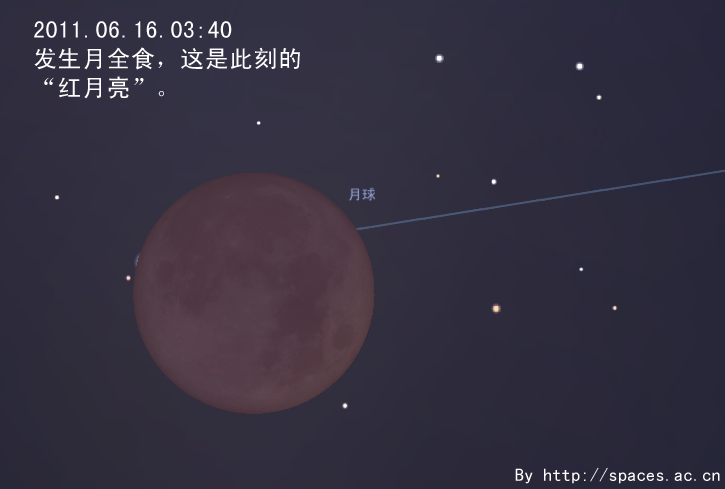
By 苏剑林 | 2011-05-28 | 26361位读者 | 引用
月全食-201106160340
6月中下旬，是北半球一年中黑夜最短的时期。今年6月22日是夏至节气，以北纬40°地区为例，当天天文昏影终到次日天文晨光始的间隔只有不到4小时50分钟。黑夜短暂会使我们可用于天文观测的时间缩短。但在夏至前后，午夜时分太阳也会在地平线下不太低的位置，这样我们就有可能整夜观测到一些类似国际空间站这样的低轨道人造天体。有兴趣的朋友可以查询相关的过境预报，挑战在一晚可以观测到多少次国际空间站过境这类的观测项目。发生在六月的日偏食和月全食，是今年天象的重头戏。接下来笔者就日偏食讲起，跟大家聊聊发生在6月的天象。
5
Mar
科学空间：2011年3月重要天象
By 苏剑林 | 2011-03-05 | 29703位读者 | 引用几颗经典行星，将成为3月星空剧场的主角。其中难得一见的水星将迎来一次观测条件很好的东大距，而到了下旬，土星也几乎整夜可见。随着落下时间的逐渐提前，木星的观测条件正逐渐变差。作为晨星的金星升起的时间也正不断推迟，我们将越来越难观测到它的身影。
天象大观
01日 11:40 金星合月: 1.7° S
11日 12:35 月合昴宿星团: 1.8° N
16日 04:16 水星合木星: 2° N
21日 07:21 春分
21日 19:00 月合角宿一: 2.5° N
21日 19:54 天王星合日
23日 08:59 水星大距: 18.6° E
31日 21:25 金星合月: 6.6° S
12
Mar
历史上的谜案——刘徽有没有使用外推法？
By 苏剑林 | 2011-03-12 | 29748位读者 | 引用
刘徽
话说当年我国古代数学家刘徽创立“割圆术”计算圆周率的事迹，在今天已被不少学生知晓；虽不能说家喻户晓，但是也为各教科书以及老师津津乐道。和古希腊的“数学之神”阿基米德同出一辙，刘徽也是使用圆的内接、外切正多边形来逼近圆形的；不一样的是，刘徽使用的方法是计算半径为1的圆的内接、外切正多边形的面积，而阿基米德计算的则是直径为1的圆的内接、外切正多边形的周长。两者的计算效果有什么区别呢？其实阿基米德的方法应该更快一点，阿基米德算到正n边形所得到的值，相当于刘徽算到正2n边形了。
在此我们不再对两者的计算方法进行区分，因为两者的本质都是一样的。按照现代数学的写法，“割圆术”的理论依据是
$$lim_{n\to \infty} n \sin(\frac{\pi}{n})=\pi\tag{1}$$
当然，刘徽不可能有现代计算正弦函数值的公式（现在计算正弦函数值一般用泰勒级数展开，而泰勒级数展开需要用到$\pi$的值），甚至在他那个时代就连笔墨也没有，据我所知即使是后来的祖冲之推算圆周率时，唯一的计算工具也只是现在称为“算筹”的小棍。不过刘徽还是凭借着超强的毅力，利用递推的方法逐步求圆周率。
20
Mar
最近评论