把地球放到“宇宙中心”...
By 苏剑林 | 2010-02-21 | 39258位读者 |虽然地心说早已站不住脚了,但是我们的确是站在地球上观测宇宙的,我们得把地球视为静止的,才能满足我们日常的观测所需。也就是说,必须得以地球为参照系。这样,我们其实也就重新树立了地球的“宇宙中心”地位。最典型的模型就是所谓的天球坐标系,它的本质就是把地球看做宇宙的中心...
从物理的角度来看,参考系的选择是随意的,等价于数学上坐标系的选择也是很随意的。有些时候,把地球看作“宇宙中心”,会给一些问题带来方便。不过要注意的是,我不是推崇地心说,而是仅仅选择了地球作为参考系!让我们来看看在这种情况下,火星的轨道如何?
首先我们来讨论一下参考系变换问题:在一个直角坐标系中,两个不同的质点$m_1,m_2$的运动轨迹分别为$[x(t),y(t)]$和$[X(t),Y(t)]$,那么,如果以$m_1$作为原点(也就是以$m_1$为参照系),那么$m_2$的轨迹变为$[X(t)-x(t),Y(t)-y(t)]$。原来的原点是静止的,但是选择了$m_1$为参照系之后就变成运动的,轨迹变为$[-x(t),-y(t)]$
我们不妨把火星和地球的轨道看做以太阳为圆心的正圆,并且以冲的位置(也就是三星成一线)作为X轴,那么可以很容易得出行星运动方程(以太阳为参照系)
火星的:
$$\begin{aligned}x=R_m \cos(\frac{v_m t}{R})=R_m \cos(\frac{2\pi t}{T_e}) \\ y=R_m \sin(\frac{v_m t}{R})=R_m \sin(\frac{2\pi t}{T_e})\end{aligned}$$
地球的:
$$\begin{aligned}x=R_e \cos(\frac{v_e t}{R})=R_e \cos(\frac{2\pi t}{T_e}) \\ y=R_e \sin(\frac{v_e t}{R})=R_e \sin(\frac{2\pi t}{T_e})\end{aligned}$$
要是选择地球为参照系,则运动轨迹由下列参数方程得出:
$$\begin{aligned}x=R_m \cos(\frac{2\pi t}{T_e})-R_e \cos(\frac{2\pi t}{T_e}) \\ y=R_m \sin(\frac{2\pi t}{T_e})-R_e \sin(\frac{2\pi t}{T_e})\end{aligned}$$
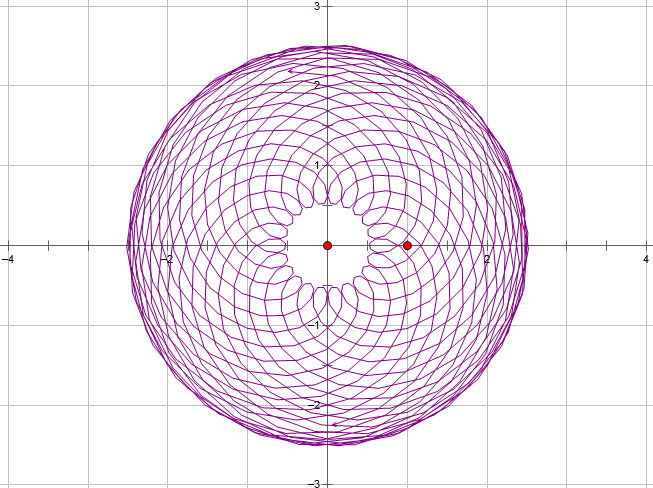
这样是一条怎样的曲线呢?把数据输入,可以得出这样的一个曲线(原点是地球):
(如此看来,地心说是一个非常不明智的选择...)
我们把上述参数方程两边平方,然后相加,可以得到:
$$x^2+y^2=R_m^2+R_e^2-2R_m R_m \cos(\frac{2\pi t}{T_e}-\frac{2\pi t}{T_m})$$
其中$x^2+y^2$即是火星到地球的距离的平方,它是关于时间t的函数
我们可以求得当$t=\frac{1}{1/{T_e}-1/{T_m}}$时,上式左端取得最小值,换句话说,(地外的)行星“冲”后$\frac{1}{1/{T_e}-1/{T_m}}$的时候,再次迎来“冲”。
当$\frac{2\pi t}{T_e}-\frac{2\pi t}{T_m}=\frac{\pi}{2}$时,即$t=\frac{1}{4(1/{T_e}-1/{T_m})}$,上式左端取得最大值,换句话说,行星“冲”后$\frac{1}{4(1/{T_e}-1/{T_m})}$的时候,迎来“合”。
转载到请包括本文地址:https://spaces.ac.cn/archives/477
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Feb. 21, 2010). 《把地球放到“宇宙中心”... 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/477
@online{kexuefm-477,
title={把地球放到“宇宙中心”...},
author={苏剑林},
year={2010},
month={Feb},
url={\url{https://spaces.ac.cn/archives/477}},
}










February 22nd, 2010
I
这图相当于:太阳绕地球作圆周运动,火星同时绕太阳作圆周运动。
II
另外想到一个问题:地球绕太阳公转的轨道平面(黄道平面)跟火星绕太阳公转的轨道平面(称之为火星黄道平面?)两者之间应该有个夹角的吧?
@II 这个只是考虑一级近似,描绘出大致形状,夹角很小忽略,精确描述还要考虑很多...