5
Mar
科学空间：2011年3月重要天象
By 苏剑林 | 2011-03-05 | 30853位读者 | 引用几颗经典行星，将成为3月星空剧场的主角。其中难得一见的水星将迎来一次观测条件很好的东大距，而到了下旬，土星也几乎整夜可见。随着落下时间的逐渐提前，木星的观测条件正逐渐变差。作为晨星的金星升起的时间也正不断推迟，我们将越来越难观测到它的身影。
天象大观
01日 11:40 金星合月: 1.7° S
11日 12:35 月合昴宿星团: 1.8° N
16日 04:16 水星合木星: 2° N
21日 07:21 春分
21日 19:00 月合角宿一: 2.5° N
21日 19:54 天王星合日
23日 08:59 水星大距: 18.6° E
31日 21:25 金星合月: 6.6° S
20
Mar
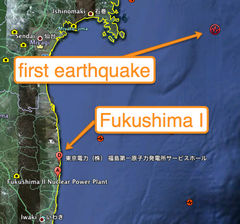
【福岛核电站】“最坏情况”有多坏？
By 苏剑林 | 2011-03-20 | 25345位读者 | 引用
5
Apr
重提“旋转弹簧伸长”问题（变分解法）
By 苏剑林 | 2011-04-05 | 20375位读者 | 引用感谢Awank-Newton读者的来信，本文于2013.01.30作了修正，主要是弹性势能的正负号问题。之前连续犯了两个错误，导致得出了正确答案。现在已经修正。参考《平衡态公理的修正与思考》
在下面的两篇文章中，BoJone已经介绍了这个“旋转弹簧伸长”的问题，并从两个角度提供了两种解答方法。前者列出了一道积分方程，然后再转变为微分方程来解；后者直接从弹性力学的角度来列出一道二阶微分方程，两者殊途同归。
http://kexue.fm/archives/782/
今天，再经过一段时间的变分法涉猎后，BoJone尝试从变分的角度（总能量最小）来给出一种新的解法。同样设r为旋转达到平衡后弹簧上一点到旋转中心的距离，该点的线密度为$\lambda =\lambda (r)$，该点到中心的弹簧质量为$m=m(r)$，旋转前的长度为$l_0$，旋转平衡后的长度为$l_1$。由于弹簧旋转后已经达到了平衡状态，由平衡态公理（参看《自然极值》系列），平衡意味着总能量“动能-势能”取极值。
23
Apr
2010年广东省高中学生化学竞赛试题和答案
By 苏剑林 | 2011-04-23 | 22723位读者 | 引用
23
Apr
看完了刘亦菲版《倩女幽魂》
By 苏剑林 | 2011-04-23 | 32238位读者 | 引用自《仙剑奇侠传1》开始，BoJone一直都有追看刘亦菲和胡歌的影视作品，尤其是古装片。胡歌版的《神雕英雄传》、《仙剑奇侠传3》连续剧分别只花了4天时间就把它们看完了（有点狂...），还有他的《神话》等。至于刘亦菲，在我的印象里她这两年没有拍过古装片了，上一部好像就是《功夫之王》了，不过这部电影我不大喜欢（有点看不懂...）。不过刘亦菲的几部古装连续剧，如《神雕侠侣》、《天龙八部》还有《仙剑奇侠传1》中的“神仙姐姐”形象颇让人深刻，也许这正是她的清纯气质吧。
倩女幽魂
我记得去年就在广州日报上看到新版《倩女幽魂》的拍摄消息了，一直都有关注其拍摄进度。好像是在本月初就定下4月22日公映了，但事实上提前公映了。据说影迷本对这部影片不抱太大希望，但是上映后人们大都改观了，好评很多，票房也一路飙升。
其实BoJone是不懂得去欣赏一部电影的。只要影片中的情节不是特别地烂，我都觉得影片不错。看了这句话，一些资深影迷基本可以忽略我了，因为本文几乎没有什么可参考的价值。^_^
29
Apr
从对称角度看代数方程
By 苏剑林 | 2011-04-29 | 26470位读者 | 引用
大马国油双峰塔
这些日子来，BoJone迷上了两个东西：最小作用量和对称。这两个“东西”在物理学中几乎占据着最重要的地位，前边已经说过，通过最小作用量原理能够构建起当代整个物理学的框架，体现着自然界的“经济头脑”；后者则是守恒的体现，也对应着自然界的“美感”。本文主要是从最简单的层面谈谈对称。
对称的东西很重要，很美。当然，这里所指的是数学上的对称。数学上有很多问题都可以列出对称的式子，而且由于其对称性，因此求解过程一般比不对称的式子简单不少。据说，当代最前沿的物理学框架都是用群论描述的（包括广义相对论），而群论正是用来研究对称的有力工具，可见，对称和对称的方法在实际中有着广泛的应用。（当然本文不讨论群论，关键是BoJone也不懂群论...^_^）
我们先来看二次方程，根据韦达定理，二次方程都可以表达成下面的形式：
$$\begin{aligned}x_1+x_2=a \\ x_1 x_2=b\end{aligned}$$
这是一个多对称的形式！这里的对称体现在将$x_1,x_2$互相替换后方程形式依然不变。如果我们设$x_1=y_1+y_2,x_2=y_1-y_2$，就可以变成
$$2y_1=a,y_1^2-y_2^2=b$$
这样很快就求出$y_1,y_2$了，继而能够求出方程的两个根。
28
May
两本通俗读物：混沌和对称
By 苏剑林 | 2011-05-28 | 17949位读者 | 引用第一本：《天遇——混沌与稳定性的起源》
一个天体力学中的N体问题的研究，竟然发展出了如此多的现代数学理论，这不能不说是一个令人意外的事情。而事实上，N体问题至今仍是无解，这也许并非坏事，因为未被完全攻克，就意味着“N体问题”仍然还是一只“会下金蛋的母鸡”！
本书是普林斯顿文集之一。作者通过大众化的语言，叙述了天体力学和动力系统理论的历史发展，让读者感到其中那激动人心的故事。BoJone认为，要想了解分析动力学（尤其是天体力学）的发展，本书是一本难得的读物。作为混沌和稳定性理论的入门前读物，本书也是非常适合的。读历史的关键是：学会思想！
6
Jun
只要我们曾经拥有过——《萍聚》
By 苏剑林 | 2011-06-06 | 22311位读者 | 引用这首歌是凤儿介绍的，去年我们学校高一夏令营的“主题歌曲”。她说歌词写得很好，我感觉也挺不错的^_^
萍，指的是漂浮在水面上的一种藻类，风吹过来，它们就会在风的作用力下聚在一起。人好象是浮在水面上的荷叶，聚散不过都是风吹动所致，到处飘散而已。因此便有了“萍水相逢”这一成语，指的是无心的邂逅或偶然的相遇。“萍聚”亦然。
曾有宋词写道“风中柳絮水中萍,聚散两无情”，这便让我们倍感人生悲欢离合的无奈。在这个充斥着高考的离别的六月里，离愁味道更浓了。可是，不论如何，明天的事情与我们无关，我们要珍惜今天事，珍惜今天人，尽我所能把握好我所拥有的。正如——
Cherish someone special for you and let them know you cherish them.
这样，当我们真的面临无可奈何的离别时，也能够含泪而微笑地挥手，唱着“只要我们曾经拥有过...”。这就是《萍聚》的声音！
最近评论