科学空间|Scientific Spaces

众所周知，分类模型通常都是先得到编码向量，然后接一个Dense层预测每个类别的概率，而预测时则是输出概率最大的类别。但大家是否想过这样一种可能：训练好的分类模型可能存在“无法预测的类别”，即不管输入是什么，都不可能预测出某个类别$k$，类别$k$永远不可能成为概率最大的那个。

当然，这种情况一般只出现在类别数远远超过编码向量维度的场景，常规的分类问题很少这么极端的。然而，我们知道语言模型本质上也是一个分类模型，它的类别数也就是词表的总大小，往往是远超过向量维度的，那么我们的语言模型是否有“无法预测的词”？（只考虑Greedy解码）

是否存在

ACL2022的论文《Low-Rank Softmax Can Have Unargmaxable Classes in Theory but Rarely in Practice》首先探究了这个问题，正如其标题所言，答案是“理论上存在但实际出现概率很小”。

点击阅读全文...

最近在用VAE处理一些文本问题的时候遇到了对离散形式的后验分布求期望的问题，于是沿着“离散分布 + 重参数”这个思路一直搜索下去，最后搜到了Gumbel Softmax，从对Gumbel Softmax的学习过程中，把重参数的相关内容都捋了一遍，还学到一些梯度估计的新知识，遂记录在此。

文章从连续情形出发开始介绍重参数，主要的例子是正态分布的重参数；然后引入离散分布的重参数，这就涉及到了Gumbel Softmax，包括Gumbel Softmax的一些证明和讨论；最后再讲讲重参数背后的一些故事，这主要跟梯度估计有关。

基本概念

重参数（Reparameterization）实际上是处理如下期望形式的目标函数的一种技巧：
\begin{equation}L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\label{eq:base}\end{equation}
这样的目标在VAE中会出现，在文本GAN也会出现，在强化学习中也会出现（$f(z)$对应于奖励函数），所以深究下去，我们会经常碰到这样的目标函数。取决于$z$的连续性，它对应不同的形式：
\begin{equation}\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\end{equation}
当然，离散情况下我们更喜欢将记号$z$换成$y$或者$c$。

点击阅读全文...

能提升模型性能的方法有很多，多任务学习（Multi-Task Learning）也是其中一种。简单来说，多任务学习是希望将多个相关的任务共同训练，希望不同任务之间能够相互补充和促进，从而获得单任务上更好的效果（准确率、鲁棒性等）。然而，多任务学习并不是所有任务堆起来就能生效那么简单，如何平衡每个任务的训练，使得各个任务都尽量获得有益的提升，依然是值得研究的课题。

最近，笔者机缘巧合之下，也进行了一些多任务学习的尝试，借机也学习了相关内容，在此挑部分结果与大家交流和讨论。

加权求和

从损失函数的层面看，多任务学习就是有多个损失函数$\mathcal{L}_1,\mathcal{L}_2,\cdots,\mathcal{L}_n$，一般情况下它们有大量的共享参数、少量的独立参数，而我们的目标是让每个损失函数都尽可能地小。为此，我们引入权重$\alpha_1,\alpha_2,\cdots,\alpha_n\geq 0$，通过加权求和的方式将它转化为如下损失函数的单任务学习
\begin{equation}\mathcal{L} = \sum_{i=1}^n \alpha_i \mathcal{L}_i\label{eq:w-loss}\end{equation}
在这个视角下，多任务学习的主要难点就是如何确定各个$\alpha_i$了。

点击阅读全文...

时至目前为止，理论物理上最深奥的问题之一，就是调和广义相对论与量子力学，而一个令物理学家们无比兴奋的，同时也争论不休的量子引力新模型，是否能重新书写物理学理论？针对不久前诞生于美国劳伦斯伯克利实验室的“霍扎瓦模型”，美国得克萨斯A&M大学科学家对其进一步研究后得出中肯的结论，并将结果与值得商榷的内容发表于8月24日出版的《物理评论快报》杂志。

量子引力的新曙光

量子引力主要就是尝试将量子力学与广义相对论合并在一起，描述对重力场进行量子化，属于万有理论之一隅。但应该如何结合，又如何让二者在微观长度等级下维持正确性，以及任何候选的量子引力论又能提供什么样可证实的预测，这是当前的物理学悬而未决的问题。遗憾的是，量子引力所探讨的能量与尺度，乃是此前实验室条件下无法观测得到的，尽管可能，且可以透过天文观测来检验，但仍属少数特例，关于量子引力理论发展上的提示一直未能成功。

点击阅读全文...

写在前面：本文是笔者数学建模课的作业，探讨了两生物种群竞争的常微分方程组模型的解的性质，展示了微分方程定性理论的基本思想。当然，本文最重要的目的，是展示LaTeX与Python的完美结合。（本文的图均由Python的Matplotlib模块生成；而文档则采用LaTeX编辑。）

问题提出

研究在同一个自然环境中生存的两个种群之间的竞争关系。假设两个种群独自在这个自然环境中生存时数量演变都服从Logistic规律，又假设当它们相互竞争时都会减慢对方数量的增长，增长速度的减小都与它们数量的乘积成正比。按照这样的假设建立的常微分方程模型为
$$\begin{equation}\label{eq:jingzhengfangcheng}\left\{\begin{aligned}\frac{dx_1}{dt}=r_1 x_1\left(1-\frac{x_1}{N_1}\right)-a_1 x_1 x_2 \\
\frac{dx_2}{dt}=r_2 x_2\left(1-\frac{x_2}{N_2}\right)-a_2 x_1 x_2\end{aligned}\right.\end{equation}$$
本文分别通过定量和定性两个角度来分析该方程的性质。

点击阅读全文...

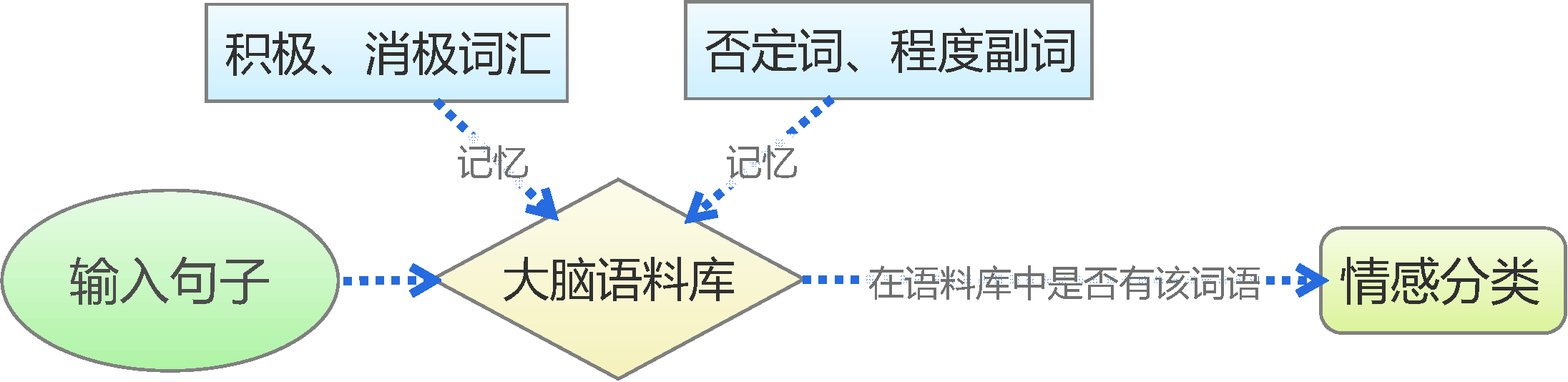
前言：四五月份的时候，我参加了两个数据挖掘相关的竞赛，分别是物电学院举办的“亮剑杯”，以及第三届 “泰迪杯”全国大学生数据挖掘竞赛。很碰巧的是，两个比赛中，都有一题主要涉及到中文情感分类工作。在做“亮剑杯”的时候，由于我还是初涉，水平有限，仅仅是基于传统的思路实现了一个简单的文本情感分类模型。而在后续的“泰迪杯”中，由于学习的深入，我已经基本了解深度学习的思想，并且用深度学习的算法实现了文本情感分类模型。因此，我打算将两个不同的模型都放到博客中，供读者参考。刚入门的读者，可以从中比较两者的不同，并且了解相关思路。高手请一笑置之。

基于情感词典

人的最简单的判断思维

点击阅读全文...

很多人觉得“模型”、“大数据”、“机器学习”这些字眼很高大很神秘，事实上，它跟我们生活中选水果差不了多少。本文用了几千字，来试图教会大家怎么选芒果...

模型的比喻

芒果

假如我要从一批芒果中，找出好吃的那个来。而我不能直接切开芒果尝尝，所以我只能观察芒果，能观察到的量有颜色、表面的气味、大小等等，这些就是我们能够收集到的信息（特征）。

生活中还要很多这样的例子，比如买火柴（可能年轻的城里人还没见过火柴？），如何判断一盒火柴的质量？难道要每根火柴都划划，看看着不着火？显然不行，我们最多也只能划几根，全部划了，火柴也不成火柴了。当然，我们还能看看火柴的样子，闻闻火柴的气味，这些动作是可以接受的。

点击阅读全文...

语言处理

在《文本情感分类（一）：传统模型》一文中，笔者简单介绍了进行文本情感分类的传统思路。传统的思路简单易懂，而且稳定性也比较强，然而存在着两个难以克服的局限性：一、精度问题，传统思路差强人意，当然一般的应用已经足够了，但是要进一步提高精度，却缺乏比较好的方法；二、背景知识问题，传统思路需要事先提取好情感词典，而这一步骤，往往需要人工操作才能保证准确率，换句话说，做这个事情的人，不仅仅要是数据挖掘专家，还需要语言学家，这个背景知识依赖性问题会阻碍着自然语言处理的进步。

点击阅读全文...