“维度灾难”之Hubness现象浅析

这几天读到论文《Exploring and Exploiting Hubness Priors for High-Quality GAN Latent Sampling》，了解到了一个新的名词“Hubness现象”，说的是高维空间中的一种聚集效应，本质上是“维度灾难”的体现之一。论文借助Hubness的概念得到了一个提升GAN模型生成质量的方案，看起来还蛮有意思。所以笔者就顺便去学习了一下Hubness现象的相关内容，记录在此，供大家参考。

坍缩的球 #

“维度灾难”是一个很宽泛的概念，所有在高维空间中与相应的二维、三维空间版本出入很大的结论，都可以称之为“维度灾难”，比如《n维空间下两个随机向量的夹角分布》中介绍的“高维空间中任何两个向量几乎都是垂直的”。其中，有不少维度灾难现象有着同一个源头——“高维空间单位球与其外切正方体的体积之比逐渐坍缩至0”，包括本文的主题“Hubness现象”亦是如此。

在《鬼斧神工：求n维球的体积》中，我们推导过$n$维球的体积公式，从中可知$n$维单位球的体积为
\begin{equation}V_n = \frac{\pi^{n/2}}{\Gamma\left(\frac{n}{2}+1\right)}\end{equation}
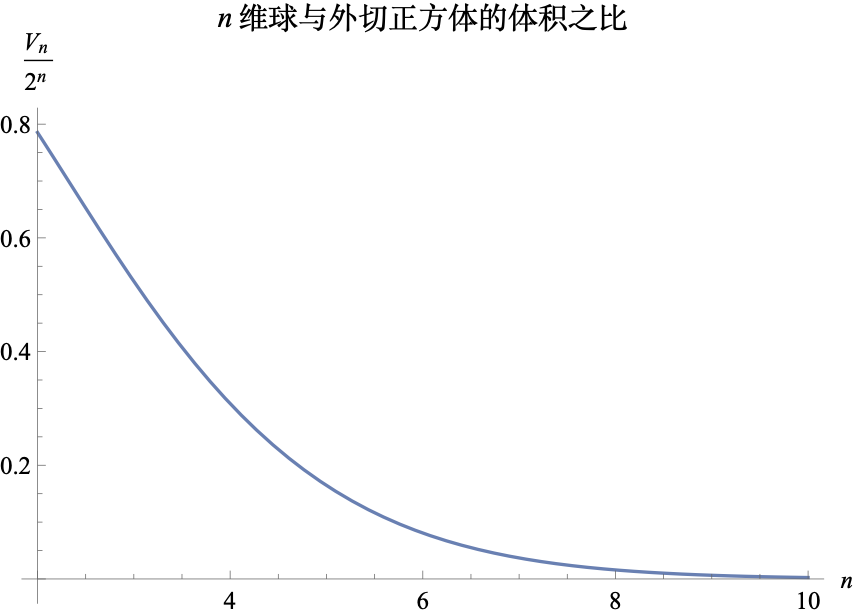
对应的外切正方体边长为$2$，体积自然为$2^n$，所以对应的体积比为$V_n / 2^n$，其图像如下图：

可以看到，随着维度的增大，这个比例很快就趋于0了。这个结论的一个形象说法是“随着维度增加，球变得越来越微不足道”，它告诉我们，如果通过“均匀分布 + 拒绝采样”的方式去实现球内的均匀采样，那么在高维空间中效率将会非常低（拒绝率接近100%）。还有一种理解方式是“高维球内的点大部分都集中在球表面附近”，球中心到球表面附近的区域占比越来越小。

Hubness现象 #

现在我们转到Hubness现象，它说的是在高维空间中随机选一批点，那么“总有一些点经常出现在其他点的$k$邻近中”。

具体怎么理解这句话呢？假设我们有$N$个点$x_1,x_2,\cdots,x_N$，对于每个$x_i$，我们都可以找出与之最相近的$k$个点，这$k$个点都称为“$x_i$的$k$邻近”。有了$k$邻近的概念后，我们可以统计每个点出现在其他点的$k$邻近的次数，这个次数称为“Hub值”，也就是说Hub值越大，它就越容易出现在其他点的$k$邻近中。

所以，Hubness现象说的是：总有那么几个点，它的Hub值显然特别大。如果Hub值代表着“财富”，那么一个形象的比喻就是“80%的财富集中在20%的人手中”，并且随着维度增大，这个“贫富差距”就越来越大；如果Hub值代表着“人脉”，那么也可以形象地比喻为“社群中总有那么几个人拥有非常广泛的人脉资源”。

Hubness现象是怎么出现的呢？其实也跟前一节说的$n$维球的坍缩有关。我们知道，与所有点距离平方和最小的点，正好是均值点：
\begin{equation}\frac{1}{N} \sum_{i=1}^N x_i = c^* = \mathop{\text{argmin}}_c \sum_{i=1}^N \Vert x_i - c\Vert^2\end{equation}
这也就意味着，在均值向量附近的点，与所有点的平均距离较小，有更大的机会成为更多点的$k$邻近。而$n$维球的坍缩现象则告诉我们，“均值向量附近的点”，即以均值向量为球心的一个球邻域，其占比是非常小的。于是就出现了“非常少的点出现在很多点的$k$邻近中”这一现象了。当然，这里的均值向量是比较直观的理解，在一般的数据点中，应该是越靠近密度中心的点，其Hub值会变得越大。

提升采样 #

那么本文开头说的提升GAN模型生成质量的方案，跟Hubness现象又有什么关系呢？论文《Exploring and Exploiting Hubness Priors for High-Quality GAN Latent Sampling》提出了一个先验假设：Hub值越大，对应点的生成质量就越好。

具体来说，一般GAN的采样生成流程是$z\sim \mathcal{N}(0,1), x=G(z)$，我们可以从$\mathcal{N}(0,1)$中先采样$N$个样本点$z_1,z_2,\cdots,z_N$，然后就可以算出每个样本点的Hub值，原论文发现Hub值跟生成质量是正相关的，所以只保留Hub值大于等于阈值$t$的样本点用来做生成。这是一种“事前”的筛选思路，参考代码如下：

def get_z_samples(size, t=50):
    """通过Hub值对采样结果进行筛选
    """
    Z = np.empty((0, z_dim))
    while len(Z) < size:
        z = np.random.randn(10000, z_dim)
        s = np.zeros(10000)
        for i in range(10):
            zi = z[i * 1000:(i + 1) * 1000]
            d = (z**2).sum(1)[:, None] + (zi**2).sum(1)[None] - 2 * z.dot(zi.T)
            for j in d.argsort(0)[1:1 + 5].T:
                s[j] += 1
        z = z[s > t]
        Z = np.concatenate([Z, z], 0)[:size]
        print('%s / %s' % (len(Z), size))
    return Z

为什么通过Hub值来筛选呢？由前面的讨论可以知道，Hub值越大，那么就越接近样本中心，其实更准确率来说是接近密度中心，意味着周围有很多临近点，那么它就不大可能是没有被充分训练的离群点，因此采样质量相对高一些。论文的多个实验结果肯定了这一结论。

文章小结 #

本文主要简介了“维度灾难”中的Hubness现象，并介绍了它在提升GAN生成质量方面的应用。

转载到请包括本文地址：https://spaces.ac.cn/archives/9147

更详细的转载事宜请参考：《科学空间FAQ》