科学空间|Scientific Spaces

本来笔者已经决心不玩RNN了，但是在上个星期思考时忽然意识到RNN实际上对应了ODE（常微分方程）的数值解法，这为我一直以来想做的事情——用深度学习来解决一些纯数学问题——提供了思路。事实上这是一个颇为有趣和有用的结果，遂介绍一翻。顺便地，本文也涉及到了自己动手编写RNN的内容，所以本文也可以作为编写自定义的RNN层的一个简单教程。

注：本文并非前段时间的热点“神经ODE”的介绍（但有一定的联系）。

RNN基本

什么是RNN？

众所周知，RNN是“循环神经网络（Recurrent Neural Network）”，跟CNN不同，RNN可以说是一类模型的总称，而并非单个模型。简单来讲，只要是输入向量序列$(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_T)$，输出另外一个向量序列$(\boldsymbol{y}_1,\boldsymbol{y}_2,\dots,\boldsymbol{y}_T)$，并且满足如下递归关系
$$\boldsymbol{y}_t=f(\boldsymbol{y}_{t-1}, \boldsymbol{x}_t, t)\tag{1}$$
的模型，都可以称为RNN。也正因为如此，原始的朴素RNN，还有改进的如GRU、LSTM、SRU等模型，我们都称为RNN，因为它们都可以作为上式的一个特例。还有一些看上去与RNN没关的内容，比如前不久介绍的CRF的分母的计算，实际上也是一个简单的RNN。

说白了，RNN其实就是递归计算。

点击阅读全文...

搞计算机视觉的朋友会知道，AM-Softmax是人脸识别中的成果。所以这篇文章就是借鉴人脸识别的做法来做句子相似度模型，顺便介绍在Keras下各种margin loss的写法。

背景

细想之下会发现，句子相似度与人脸识别有很多的相似之处～

已有的做法

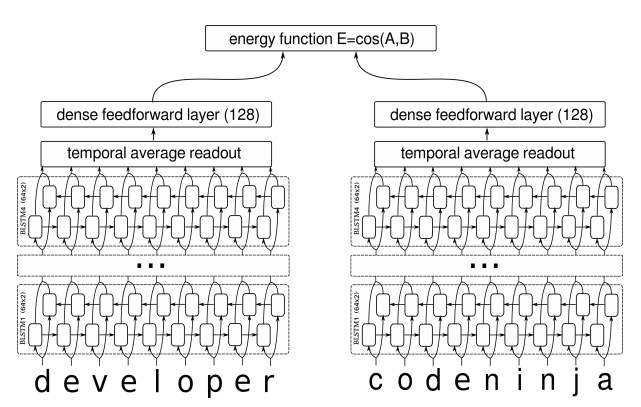
在我搜索到的资料中，深度学习做句子相似度模型，就只有两种做法：一是输入一对句子，然后输出一个0/1标签代表相似程度，也就是视为一个二分类问题，比如《Learning Text Similarity with Siamese Recurrent Networks》中的模型是这样的

将句子相似度视为二分类模型

包括今年拍拍贷的“魔镜杯”，也是这种格式。另外一种做法是输入一个三元组“（句子A，跟A相似的句子，跟A不相似的句子）”，然后用triplet loss的做法解决，比如文章《Applying Deep Learning To Answer Selection: A Study And An Open Task》中的做法。

这两种做法其实也可以看成是一种，本质上是一样的，只不过loss和训练方法有所差别。但是，这两种方法却都有一个很严重的问题：负样本采样严重不足，导致效果提升非常慢。

点击阅读全文...

在这个系列中，我们来关心优化算法，而本文的主题则是SGD（stochastic gradient descent，随机梯度下降），包括带Momentum和Nesterov版本的。对于SGD，我们通常会关心的几个问题是：

SGD为什么有效？
SGD的batch size是不是越大越好？
SGD的学习率怎么调？
Momentum是怎么加速的？
Nesterov为什么又比Momentum稍好？
...

这里试图从动力学角度分析SGD，给出上述问题的一些启发性理解。

梯度下降

既然要比较谁好谁差，就需要知道最好是什么样的，也就是说我们的终极目标是什么？

训练目标分析

假设全部训练样本的集合为$\boldsymbol{S}$，损失度量为$L(\boldsymbol{x};\boldsymbol{\theta})$，其中$\boldsymbol{x}$代表单个样本，而$\boldsymbol{\theta}$则是优化参数，那么我们可以构建损失函数
$$L(\boldsymbol{\theta}) = \frac{1}{|\boldsymbol{S}|}\sum_{\boldsymbol{x}\in\boldsymbol{S}} L(\boldsymbol{x};\boldsymbol{\theta})\tag{1}$$
而训练的终极目标，则是找到$L(\boldsymbol{\theta})$的一个全局最优点（这里的最优是“最小”的意思）。

点击阅读全文...

前言：我小学开始就喜欢纯数学，后来也喜欢上物理，还学习过一段时间的理论物理，直到本科毕业时，我才慢慢进入机器学习领域。所以，哪怕在机器学习领域中，我的研究习惯还保留着数学和物理的风格：企图从最少的原理出发，理解、推导尽可能多的东西。这篇文章是我这个理念的结果之一，试图以变分推断作为出发点，来统一地理解深度学习中的各种模型，尤其是各种让人眼花缭乱的GAN。本文已经挂到arxiv上，需要读英文原稿的可以移步到《Variational Inference: A Unified Framework of Generative Models and Some Revelations》。

下面是文章的介绍。其实，中文版的信息可能还比英文版要稍微丰富一些，原谅我这蹩脚的英语...

摘要：本文从一种新的视角阐述了变分推断，并证明了EM算法、VAE、GAN、AAE、ALI(BiGAN)都可以作为变分推断的某个特例。其中，论文也表明了标准的GAN的优化目标是不完备的，这可以解释为什么GAN的训练需要谨慎地选择各个超参数。最后，文中给出了一个可以改善这种不完备性的正则项，实验表明该正则项能增强GAN训练的稳定性。

近年来，深度生成模型，尤其是GAN，取得了巨大的成功。现在我们已经可以找到数十个乃至上百个GAN的变种。然而，其中的大部分都是凭着经验改进的，鲜有比较完备的理论指导。

本文的目标是通过变分推断来给这些生成模型建立一个统一的框架。首先，本文先介绍了变分推断的一个新形式，这个新形式其实在博客以前的文章中就已经介绍过，它可以让我们在几行字之内导出变分自编码器（VAE）和EM算法。然后，利用这个新形式，我们能直接导出GAN，并且发现标准GAN的loss实则是不完备的，缺少了一个正则项。如果没有这个正则项，我们就需要谨慎地调整超参数，才能使得模型收敛。

点击阅读全文...

话说自称搞了这么久的NLP，我都还没有真正跑过NLP与深度学习结合的经典之作——seq2seq。这两天兴致来了，决定学习并实践一番seq2seq，当然最后少不了Keras实现了。

seq2seq可以做的事情非常多，我这挑选的是比较简单的根据文章内容生成标题（中文），也可以理解为自动摘要的一种。选择这个任务主要是因为“文章-标题”这样的语料对比较好找，能快速实验一下。

seq2seq简介

所谓seq2seq，就是指一般的序列到序列的转换任务，比如机器翻译、自动文摘等等，这种任务的特点是输入序列和输出序列是不对齐的，如果对齐的话，那么我们称之为序列标注，这就比seq2seq简单很多了。所以尽管序列标注任务也可以理解为序列到序列的转换，但我们在谈到seq2seq时，一般不包含序列标注。

要自己实现seq2seq，关键是搞懂seq2seq的原理和架构，一旦弄清楚了，其实不管哪个框架实现起来都不复杂。早期有一个第三方实现的Keras的seq2seq库，现在作者也已经放弃更新了，也许就是觉得这么简单的事情没必要再建一个库了吧。可以参考的资料还有去年Keras官方博客中写的《A ten-minute introduction to sequence-to-sequence learning in Keras》。

点击阅读全文...

沿着之前的《“让Keras更酷一些！”：精巧的层与花式的回调》写下去～

今天我们来看一个小众需求：自定义优化器。

细想之下，不管用什么框架，自定义优化器这个需求可谓真的是小众中的小众。一般而言，对于大多数任务我们都可以无脑地直接上Adam，而调参炼丹高手一般会用SGD来调出更好的效果，换言之不管是高手新手，都很少会有自定义优化器的需求。

那这篇文章还有什么价值呢？有些场景下会有一点点作用。比如通过学习Keras中的优化器写法，你可以对梯度下降等算法有进一步的认识，你还可以顺带看到Keras的源码是多么简洁优雅。此外，有时候我们可以通过自定义优化器来实现自己的一些功能，比如给一些简单的模型（例如Word2Vec）重写优化器（直接写死梯度，而不是用自动求导），可以使得算法更快；自定义优化器还可以实现诸如“软batch”的功能。

Keras优化器

我们首先来看Keras中自带优化器的代码，位于：
https://github.com/keras-team/keras/blob/master/keras/optimizers.py

点击阅读全文...

在《从动力学角度看优化算法（一）：从SGD到动量加速》一文中，我们提出SGD优化算法跟常微分方程（ODE）的数值解法其实是对应的，由此还可以很自然地分析SGD算法的收敛性质、动量加速的原理等等内容。

在这篇文章中，我们继续沿着这个思路，去理解优化算法中的自适应学习率算法。

RMSprop

首先，我们看一个非常经典的自适应学习率优化算法：RMSprop。RMSprop虽然不是最早提出的自适应学习率的优化算法，但是它却是相当实用的一种，它是诸如Adam这样的更综合的算法的基石，通过它我们可以观察自适应学习率的优化算法是怎么做的。

算法概览

一般的梯度下降是这样的：
$$\begin{equation}\boldsymbol{\theta}_{n+1}=\boldsymbol{\theta}_{n} - \gamma \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n})\end{equation}$$
很明显，这里的$\gamma$是一个超参数，便是学习率，它可能需要在不同阶段做不同的调整。

而RMSprop则是
$$\begin{equation}\begin{aligned}\boldsymbol{g}_{n+1} =& \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n})\\
\boldsymbol{G}_{n+1}=&\lambda \boldsymbol{G}_{n} + (1 - \lambda) \boldsymbol{g}_{n+1}\otimes \boldsymbol{g}_{n+1}\\
\boldsymbol{\theta}_{n+1}=&\boldsymbol{\theta}_{n} - \frac{\tilde{\gamma}}{\sqrt{\boldsymbol{G}_{n+1} + \epsilon}}\otimes \boldsymbol{g}_{n+1}
\end{aligned}\end{equation}$$

点击阅读全文...

前言：去年写过一篇WGAN-GP的入门读物《互怼的艺术：从零直达WGAN-GP》，提到通过梯度惩罚来为WGAN的判别器增加Lipschitz约束（下面简称“L约束”）。前几天遐想时再次想到了WGAN，总觉得WGAN的梯度惩罚不够优雅，后来也听说WGAN在条件生成时很难搞（因为不同类的随机插值就开始乱了...），所以就想琢磨一下能不能搞出个新的方案来给判别器增加L约束。

闭门造车想了几天，然后发现想出来的东西别人都已经做了，果然是只有你想不到，没有别人做不到。主要包含在这两篇论文中：《Spectral Norm Regularization for Improving the Generalizability of Deep Learning》和《Spectral Normalization for Generative Adversarial Networks》。

所以这篇文章就按照自己的理解思路，对L约束相关的内容进行简单的介绍。注意本文的主题是L约束，并不只是WGAN。它可以用在生成模型中，也可以用在一般的监督学习中。

L约束与泛化

扰动敏感

记输入为$x$，输出为$y$，模型为$f$，模型参数为$w$，记为
$$\begin{equation}y = f_w(x)\end{equation}$$
很多时候，我们希望得到一个“稳健”的模型。何为稳健？一般来说有两种含义，一是对于参数扰动的稳定性，比如模型变成了$f_{w+\Delta w}(x)$后是否还能达到相近的效果？如果在动力学系统中，还要考虑模型最终是否能恢复到$f_w(x)$；二是对于输入扰动的稳定性，比如输入从$x$变成了$x+\Delta x$后，$f_w(x+\Delta x)$是否能给出相近的预测结果。读者或许已经听说过深度学习模型存在“对抗攻击样本”，比如图片只改变一个像素就给出完全不一样的分类结果，这就是模型对输入过于敏感的案例。

点击阅读全文...