低秩近似之路(四):ID
By 苏剑林 | 2024-10-30 | 5194位读者 | 引用这篇文章的主角是ID(Interpolative Decomposition),中文可以称之为“插值分解”,它同样可以理解为是一种具有特定结构的低秩分解,其中的一侧是该矩阵的若干列(当然如果你偏好于行,那么选择行也没什么问题),换句话说,ID试图从一个矩阵中找出若干关键列作为“骨架”(通常也称作“草图”)来逼近原始矩阵。
可能很多读者都未曾听说过ID,即便维基百科也只有几句语焉不详的介绍(链接),但事实上,ID跟SVD一样早已内置在SciPy之中(参考scipy.linalg.interpolative),这侧面印证了ID的实用价值。
基本定义
前三篇文章我们分别介绍了伪逆、SVD、CR近似,它们都可以视为寻找特定结构的低秩近似:
\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\end{equation}
科学空间:2009年11月重要天象
By 苏剑林 | 2009-10-18 | 22053位读者 | 引用转眼间已经快到年底了,11月天象的重头戏,仍将是流星雨。2009年的狮子座流星雨,是否会出现预测的较大爆发,这个月我们将找到答案。此外,南北金牛座流星雨、麒麟座a流星雨等几个传统的流星雨也将在本月达到极大,它们同样是值得爱好者观测的目标。适合在11月观测的行星主要是木星和火星,前者的最佳观测时机是在日落后不久,而后者在下半夜的观测条件不错。
提醒各位天文爱好者一点,制定观测计划之前一定要先查看天气预报,而且在这个寒冷的季节观测流星雨,一定要注意保暖!
主要天象:
01日 火星近鬼星团
05日 南金牛座流星雨极大(ZHR=5)
09日 火星合月
12日 北金牛座流星雨极大(ZHR=5)
13日 土星合月
16日 金星合月
17日 水星合月
18日 月掩心宿二;狮子座流星雨极大(05:45, ZHR=100+)
21日 麒麟座α流星雨极大(23:25, ZHR=5~400+?)
24日 木星合月/海王星合月
27日 天王星合月
科学空间:2011年6月重要天象
By 苏剑林 | 2011-05-28 | 26473位读者 | 引用6月中下旬,是北半球一年中黑夜最短的时期。今年6月22日是夏至节气,以北纬40°地区为例,当天天文昏影终到次日天文晨光始的间隔只有不到4小时50分钟。黑夜短暂会使我们可用于天文观测的时间缩短。但在夏至前后,午夜时分太阳也会在地平线下不太低的位置,这样我们就有可能整夜观测到一些类似国际空间站这样的低轨道人造天体。有兴趣的朋友可以查询相关的过境预报,挑战在一晚可以观测到多少次国际空间站过境这类的观测项目。发生在六月的日偏食和月全食,是今年天象的重头戏。接下来笔者就日偏食讲起,跟大家聊聊发生在6月的天象。
引力透镜——用经典力学推导光的偏转公式
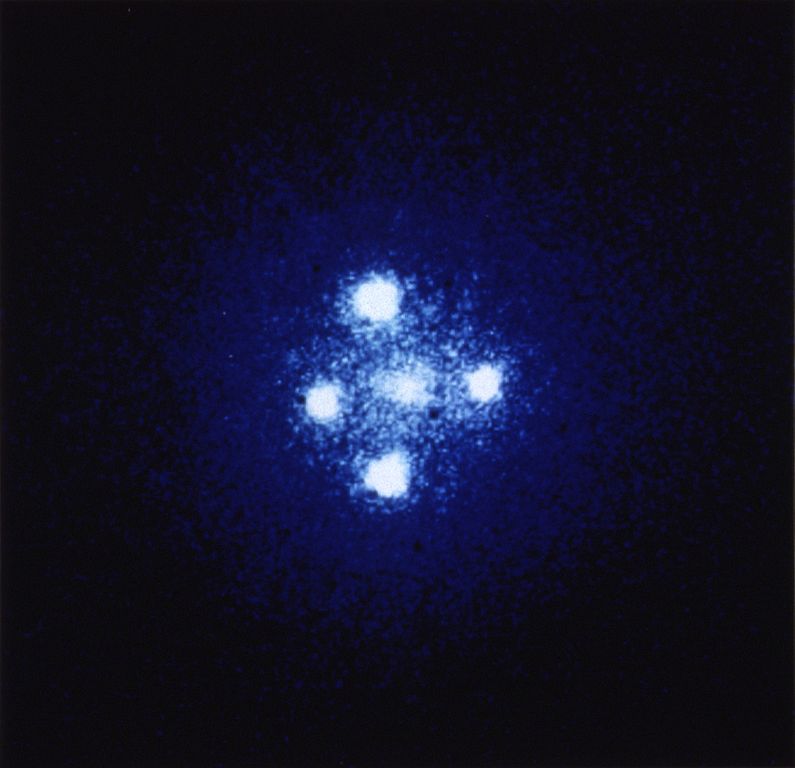
By 苏剑林 | 2012-04-30 | 62322位读者 | 引用引力透镜
————用经典力学推导光的引力偏转角公式
在2012年第四期的《天文爱好者》上,Richard de Grijs(何锐思)教授的《引力透镜——再领科学潮》一文详细而精彩地讲述了有关引力透镜方面的知识,尤其是它在天文方面的重要应用,让我收获颇丰。笔者在赞叹作者优美的文笔和译者程思浩同好的生动翻译之余,也感到了一丝不足。文章主要讲了引力透镜在天文研究中所扮演的重要角色,却未对引力透镜的原理、本质方面多加描述。时空的扭曲是广义相对论给出的答案,可是难道仅仅从经典力学就不能领略丝毫?藉此,BoJone这在里对引力透镜多说些东西,与大家相互学习研究。当然,由于我只是一个初出茅庐的业余爱好者,其中的不当之处还望各位斧正。
《新理解矩阵1》:矩阵是什么?
By 苏剑林 | 2012-10-29 | 74683位读者 | 引用前边我承诺过会写一些关于自己对矩阵的理解。其实孟岩在《理解矩阵》这三篇文章中,已经用一种很直观的方法告诉了我们有关矩阵以及线性代数的一些性质和思想。而我对矩阵的理解,大多数也是来源于他的文章。当然,为了更好地理解线性代数,我还阅读了很多相关书籍,以求得到一种符合直觉的理解方式。孟岩的blog已经很久没有更新了,在此谨引用他的标题,来叙述我对矩阵的理解。
当然,我不打算追求那些空间、算子那些高抽象性的问题,我只是想发表一下自己对线性代数中一些常用工具的看法,比如说矩阵、行列式等。同时,文章命名为“理解矩阵”,也就是说这不是矩阵入门教程,而是与已经有一定的线性代数基础的读者一起探讨关于矩阵的其他理解方式,仅此而已。我估计基本上学过线性代数的读者都能够读懂这篇文章。
首先,我们不禁要追溯一个本源问题:矩阵是什么?
从动力学角度看优化算法(一):从SGD到动量加速
By 苏剑林 | 2018-06-27 | 157010位读者 | 引用在这个系列中,我们来关心优化算法,而本文的主题则是SGD(stochastic gradient descent,随机梯度下降),包括带Momentum和Nesterov版本的。对于SGD,我们通常会关心的几个问题是:
SGD为什么有效?
SGD的batch size是不是越大越好?
SGD的学习率怎么调?
Momentum是怎么加速的?
Nesterov为什么又比Momentum稍好?
...
这里试图从动力学角度分析SGD,给出上述问题的一些启发性理解。
梯度下降
既然要比较谁好谁差,就需要知道最好是什么样的,也就是说我们的终极目标是什么?
训练目标分析
假设全部训练样本的集合为$\boldsymbol{S}$,损失度量为$L(\boldsymbol{x};\boldsymbol{\theta})$,其中$\boldsymbol{x}$代表单个样本,而$\boldsymbol{\theta}$则是优化参数,那么我们可以构建损失函数
$$L(\boldsymbol{\theta}) = \frac{1}{|\boldsymbol{S}|}\sum_{\boldsymbol{x}\in\boldsymbol{S}} L(\boldsymbol{x};\boldsymbol{\theta})\tag{1}$$
而训练的终极目标,则是找到$L(\boldsymbol{\theta})$的一个全局最优点(这里的最优是“最小”的意思)。
从DCGAN到SELF-MOD:GAN的模型架构发展一览
By 苏剑林 | 2019-04-19 | 79206位读者 | 引用事实上,O-GAN的发现,已经达到了我对GAN的理想追求,使得我可以很惬意地跳出GAN的大坑了。所以现在我会试图探索更多更广的研究方向,比如NLP中还没做过的任务,又比如图神经网络,又或者其他有趣的东西。
不过,在此之前,我想把之前的GAN的学习结果都记录下来。
这篇文章中,我们来梳理一下GAN的架构发展情况,当然主要的是生成器的发展,判别器一直以来的变动都不大。还有,本文介绍的是GAN在图像方面的模型架构发展,跟NLP的SeqGAN没什么关系。
此外,关于GAN的基本科普,本文就不再赘述了。
突破瓶颈,打造更强大的Transformer
By 苏剑林 | 2020-04-13 | 124291位读者 | 引用自《Attention is All You Need》一文发布后,基于Multi-Head Attention的Transformer模型开始流行起来,而去年发布的BERT模型更是将Transformer模型的热度推上了又一个高峰。当然,技术的探索是无止境的,改进的工作也相继涌现:有改进预训练任务的,比如XLNET的PLM、ALBERT的SOP等;有改进归一化的,比如Post-Norm向Pre-Norm的改变,以及T5中去掉了Layer Norm里边的beta参数等;也有改进模型结构的,比如Transformer-XL等;有改进训练方式的,比如ALBERT的参数共享等;...
以上的这些改动,都是在Attention外部进行改动的,也就是说它们都默认了Attention的合理性,没有对Attention本身进行改动。而本文我们则介绍关于两个新结果:它们针对Multi-Head Attention中可能存在建模瓶颈,提出了不同的方案来改进Multi-Head Attention。两篇论文都来自Google,并且做了相当充分的实验,因此结果应该是相当有说服力的了。
再小也不能小key_size
第一个结果来自文章《Low-Rank Bottleneck in Multi-head Attention Models》,它明确地指出了Multi-Head Attention里边的表达能力瓶颈,并提出通过增大key_size的方法来缓解这个瓶颈。









最近评论