科学空间|Scientific Spaces

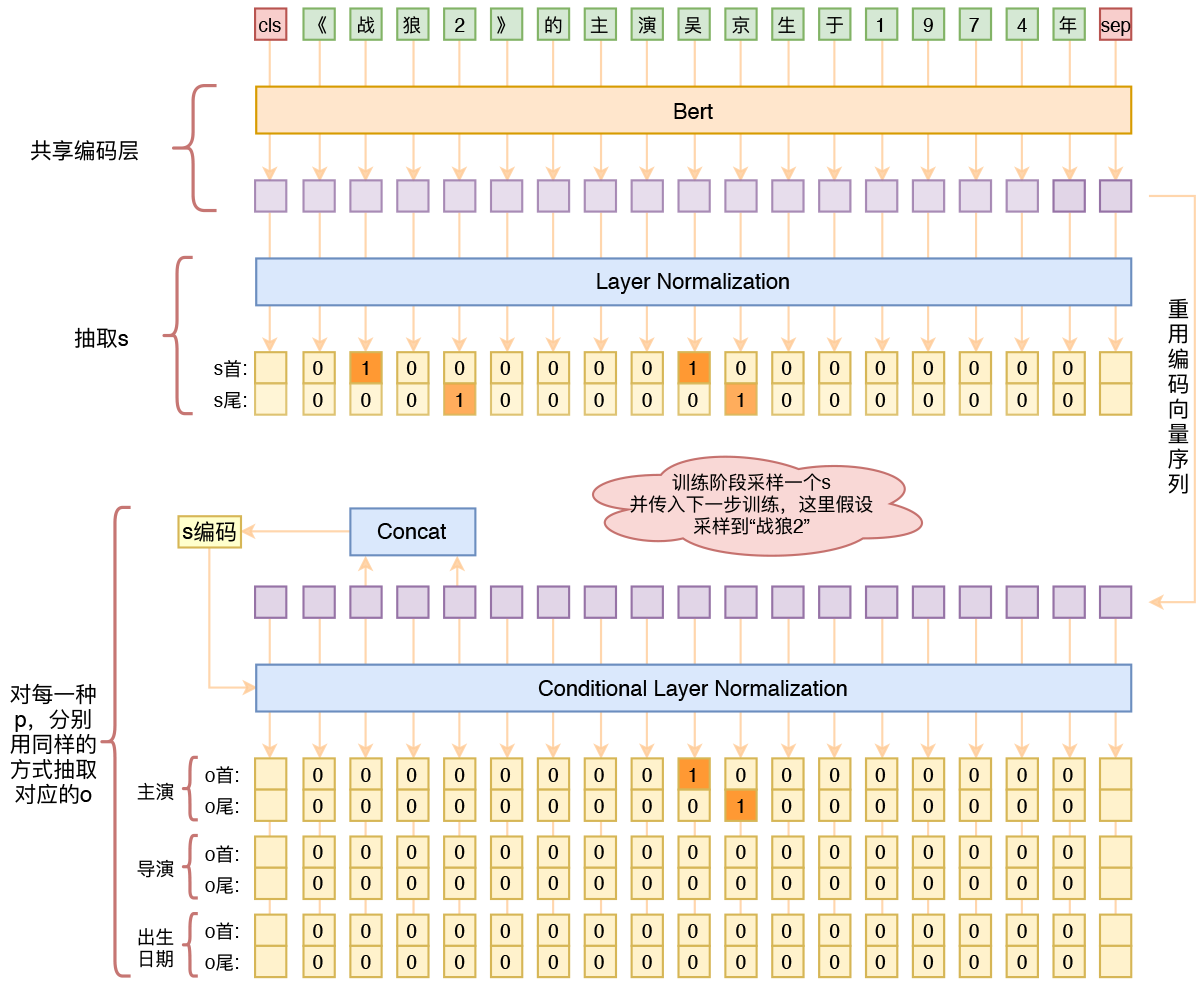
在开发bert4keras的时候就承诺过，会逐渐将之前用keras-bert实现的例子逐渐迁移到bert4keras来，而那里其中一个例子便是三元组抽取的任务。现在bert4keras的例子已经颇为丰富了，但还没有序列标注和信息抽取相关的任务，而三元组抽取正好是这样的一个任务，因此就补充上去了。

基于Bert的三元组抽取模型结构示意图

点击阅读全文...

在文章《玩转Keras之seq2seq自动生成标题》中我们已经基本探讨过seq2seq，并且给出了参考的Keras实现。

本文则将这个seq2seq再往前推一步，引入双向的解码机制，它在一定程度上能提高生成文本的质量（尤其是生成较长文本时）。本文所介绍的双向解码机制参考自《Synchronous Bidirectional Neural Machine Translation》，最后笔者也是用Keras实现的。

背景介绍

研究过seq2seq的读者都知道，常见的seq2seq的解码过程是从左往右逐字（词）生成的，即根据encoder的结果先生成第一个字；然后根据encoder的结果以及已经生成的第一个字，来去生成第二个字；再根据encoder的结果和前两个字，来生成第三个词；依此类推。总的来说，就是在建模如下概率分解
\begin{equation}p(Y|X)=p(y_1|X)p(y_2|X,y_1)p(y_3|X,y_1,y_2)\cdots\label{eq:p}\end{equation}

点击阅读全文...

中国象棋

不知道读者有没有看过量子位年初的文章《最强写作AI竟然学会象棋和作曲，语言模型跨界操作引热议，在线求战》，里边提到有网友用GPT2模型训练了一个下国际象棋的模型。笔者一直在想，这么有趣的事情怎么可以没有中文版呢？对于国际象棋来说，其中文版自然就是中国象棋了，于是我一直有想着把它的结果在中国象棋上面复现一下。拖了大半年，在最近几天终于把这个事情完成了，在此跟大家分享一下。

象棋谱式
将军不离九宫内，士止相随不出官。
象飞四方营四角，马行一步一尖冲。
炮须隔子打一子，车行直路任西东。
唯卒只能行一步，过河横进退无踪。

点击阅读全文...

相信不少读者这几天都看到了清华大学与智源人工智能研究院一起搞的“清源计划”（相关链接《中文版GPT-3来了？智源研究院发布清源 CPM —— 以中文为核心的大规模预训练模型》），里边开源了目前最大的中文GPT2模型CPM-LM（26亿参数），据说未来还会开源200亿甚至1000亿参数的模型，要打造“中文界的GPT3”。

官方给出的CPM-LM的Few Shot效果演示图

我们知道，GPT3不需要finetune就可以实现Few Shot，而目前CPM-LM的演示例子中，Few Shot的效果也是相当不错的，让人跃跃欲试，笔者也不例外。既然要尝试，肯定要将它适配到自己的bert4keras中才顺手，于是适配工作便开始了。本以为这是一件很轻松的事情，谁知道踩坑踩了快3天才把它搞好，在此把踩坑与测试的过程稍微记录一下。

点击阅读全文...

可能有读者留意到，这次更新相对来说隔得比较久了。事实上，在上周末时就开始准备这篇文章了，然而笔者低估了这个问题的难度，几乎推导了整整一周，仍然还没得到一个完善的结果出来。目前发出来的，仍然只是一个失败的结果，希望有经验的读者可以指点指点。

在文章《将“Softmax+交叉熵”推广到多标签分类问题》中，我们提出了一个多标签分类损失函数，它能自动调节正负类的不平衡问题，后来在《多标签“Softmax+交叉熵”的软标签版本》中我们还进一步得到了它的“软标签”版本。本质上来说，多标签分类就是“$n$个2分类”问题，那么相应的，“$n$个$m$分类”的损失函数又该是怎样的呢？

这就是本文所要探讨的问题。

点击阅读全文...

对于很多读者来说，生成扩散模型可能是他们遇到的第一个能够将如此多的数学工具用到深度学习上的模型。在这个系列文章中，我们已经展示了扩散模型与数学分析、概率统计、常微分方程、随机微分方程乃至偏微分方程等内容的深刻联系，可以说，即便是做数学物理方程的纯理论研究的同学，大概率也可以在扩散模型中找到自己的用武之地。

在这篇文章中，我们再介绍一个同样与数学物理有深刻联系的扩散模型——由“万有引力定律”启发的ODE式扩散模型，出自论文《Poisson Flow Generative Models》（简称PFGM），它给出了一个构建ODE式扩散模型的全新视角。

万有引力

中学时期我们就学过万有引力定律，大概的描述方式是：

两个质点彼此之间相互吸引的作用力，是与它们的质量乘积成正比，并与它们之间的距离成平方反比。

点击阅读全文...

在前面的介绍中，我们多次提及“得分匹配”和“条件得分匹配”，它们是扩散模型、能量模型等经常出现的概念，特别是很多文章直接说扩散模型的训练目标是“得分匹配”，但事实上当前主流的扩散模型如DDPM的训练目标是“条件得分匹配”才对。

那么“得分匹配”与“条件得分匹配”具体是什么关系呢？它们两者是否等价呢？本文详细讨论这个问题。

得分匹配

首先，得分匹配（Score Matching）是指训练目标：
\begin{equation}\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\left[\left\Vert\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t) - \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)\right\Vert^2\right]\label{eq:sm}\end{equation}
其中$\boldsymbol{\theta}$是训练参数。很明显，得分匹配是想学习一个模型$\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)$来逼近$\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)$，这里的$\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)$我们就称为“得分”。

点击阅读全文...

在《从熵不变性看Attention的Scale操作》、《熵不变性Softmax的一个快速推导》中笔者提出了熵不变性Softmax，简单来说就是往Softmax之前的Attention矩阵多乘上一个$\log n$，理论上有助于增强长度外推性，其中$n$是序列长度。$\log n$这个因子让笔者联系到了JL引理（Johnson-Lindenstrauss引理），因为JL引理告诉我们编码$n$个向量只需要$\mathcal{O}(\log n)$的维度就行了，大家都是$\log n$，这两者有没有什么关联呢？

熵不变性

我们知道，熵是不确定性的度量，用在注意力机制中，我们将它作为“集中注意力的程度”。所谓熵不变性，指的是不管序列长度$n$是多少，我们都要将注意力集中在关键的几个token上，而不要太过分散。为此，我们提出的熵不变性Attention形式为
\begin{equation}Attention(Q,K,V) = softmax\left(\frac{\log_{512} n}{\sqrt{d}}QK^{\top}\right)V\label{eq:core}\end{equation}

点击阅读全文...