简单得令人尴尬的FSQ：“四舍五入”超越了VQ-VAE

正如“XXX is all you need”一样，有不少论文都以“简单得令人尴尬”命名（An Embarrassingly Simple XXX），但在笔者看来，这些论文大多数都是噱头多于实力。不过，笔者最近阅读到的一篇论文，真的让人不由得发出“简单得令人尴尬”的感叹～

论文的标题是《Finite Scalar Quantization: VQ-VAE Made Simple》，顾名思义，这是一篇旨在用FSQ（Finite Scalar Quantization）简化VQ-VAE的工作。随着生成模型、多模态LLM的逐渐流行，VQ-VAE及其后续工作也作为“图像的Tokenizer”而“水涨船高”。然而，VQ-VAE的训练本身也存在一些问题，而FSQ这篇论文则声称通过更简单的“四舍五入”就可以达到同样的目的，并且有着效果更好、收敛更快、训练更稳的优点。

FSQ真有这么神奇？接下来我们一起学习一下。

VQ #

首先，我们来了解一下“VQ”。VQ全称是“Vector Quantize”，可以翻译为“向量量子化”或者“向量量化”，是指将无限、连续的编码向量映射为有限、离散的整数数字的一种技术。如果我们将VQ应用在自编码器的中间层，那么可以在压缩输入大小的同时，让编码结果成为一个离散的整数序列。

假设自编码器的重构损失能够让我们满意，那么这个整数序列就是原始图像的等价物，所有关于原始图像的操作都可以转化为整数序列上的操作。比如我们想训练图像生成模型，就只需要训练整数序列生成模型，而这跟本文生成等价，所以我们可以用它来训练一个GPT，模型和流程都跟文本一模一样，训练完成后，我们就可以从GPT模型中采样整数序列，然后送到解码器中得到图像，从而完完成了图像生成模型的构建。说白了，“VQ+自编码器”将任意输入都转化为跟文本一致的整数序列，统一了不同模态数据的输入形式，同时也统一了它们的处理和生成模型。

而这样的一个带有VQ功能的自编码器，就被称为“VQ-VAE”。

AE #

早在四年前的文章《VQ-VAE的简明介绍：量子化自编码器》中我们就介绍过了VQ-VAE，尽管被冠以“VAE（Variational AutoEncoder）”之名，但它实际上跟VAE没啥关系，如上一节所说，它只是一个带有VQ功能的AE（AutoEncoder）。

既然是AE，那么有encoder和decoder，一个普通的AE是这样的：
\begin{equation}z = encoder(x),\quad \hat{x}=decoder(z),\quad \mathcal{L}=\Vert x - \hat{x}\Vert^2 \end{equation}
VQ-VAE则稍微复杂一些：
\begin{equation}\begin{aligned}
z =&\, encoder(x)\\[5pt]
z_q =&\, z + \text{sg}[e_k - z],\quad k = \mathop{\text{argmin}}_{i\in\{1,2,\cdots,K\}} \Vert z - e_i\Vert\\
\hat{x} =&\, decoder(z_q)\\[5pt]
\mathcal{L} =&\, \Vert x - \hat{x}\Vert^2 + \beta\Vert e_k - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[e_k]\Vert^2
\end{aligned}\label{eq:vqvae}\end{equation}

让我们来逐步解释一下。首先，第一步是相同的，输入$x$到encoder中，输出编码向量$z$。然而，我们并不是直接将$z$输入到decoder中，而是先维护一个编码向量表$\{e_1,e_2,\cdots,e_K\}$（Codebook），从中选取与$z$最相近的一个$e_k$送入到decoder中进行重构$x$。由于编码表是有限的，所以我们也可以将实际的编码结果理解为一个整数（即与$z$最相近的$e_k$的$k$），这就是VQ-VAE中“VQ”的含义。

当然，实际应用中，为了保证重构的清晰度，encoder的输出可能是多个向量，每个向量经历同样的量化步骤变成一个整数，所以结果就是一张原本在连续实数空间的图片，被编码VQ-VAE编码为了一个整数的序列，这跟文本Tokenizer的作用是类似的，所以就有了“图像的Tokenizer”的说法。

梯度 #

然而，由于整个前向计算的流程中出现了$\mathop{\text{argmin}}$，所以梯度无法回传到encoder，这意味着我们无法优化encoder。此时常见的手段是Gumbel Softmax，但Gumbel Softmax的效果通常也是次优的，所以作者巧妙地借助了Straight-Through为VQ-VAE设计了更好的梯度。可以说，这是VQ-VAE最精彩的内容，它告诉我们什么“Attention is all you need”都是虚的，“Gradient”才是真正的“all we need”！

具体来说，VQ-VAE利用了深度学习框架基本上都自带的stop_gradient（即公式中的$\text{sg}$）函数来自定义梯度，所有经过$\text{sg}$的输入，都会保持同样的输出，但梯度被强迫为零。所以对于式$\eqref{eq:vqvae}$中的$z_q$，我们有
\begin{equation}z_q = e_k,\quad \nabla z_q = \nabla z\label{eq:sg}\end{equation}
这样一来，送入decoder的还是量化过后的$e_k$，但优化器求梯度时用的是$z$，而$z$是encoder出来的，所以encoder也能够被优化了。这个操作就叫做“Straight-Through Estimator（STE）”，是为神经网络的不可导模块设计梯度的常用技巧之一。

由于基于梯度的优化器依然是当前的主流，所以直接设计梯度往往比设计loss更贴近本质，当然通常也更难、更让人由衷地赞叹。

Loss #

不顾，事情还没完，此时有两个问题：1、现在encoder是有梯度了，但是编码表$e_1,e_2,\cdots,e_K$却没了梯度；2、$\text{sg}$虽然可以随意定义梯度，但不是胡乱定义一个梯度都可以成功优化模型的。从$\eqref{eq:sg}$可以看成，要使它在数学上严格成立，那么唯一的解是$e_k=z$，这告诉我们如果STE是合理的，那么$e_k$与$z$至少是相近的。于是为了梯度的合理性，同时也为了优化编码表，我们还可以补充一项辅助loss：
\begin{equation}\Vert e_k - z\Vert^2\label{eq:ez}\end{equation}
这样既可以迫使$e_k$与$z$接近，又可以让$e_k$也拥有了梯度，一举两得！但细想之下，还是有点美中不足：理论上encoder和decoder的重构loss已经足够优化$z$了，所以额外引入的一项应该主要用来优化$e_k$，而不应该反过来明显影响$z$。为此，我们再次利用$\text{sg}$技巧，不难证明式$\eqref{eq:ez}$的梯度等价于
\begin{equation}\Vert e_k - \text{sg}[z]\Vert^2 + \Vert z - \text{sg}[e_k]\Vert^2\end{equation}
第一项把$z$的梯度停掉了，剩下$e_k$的梯度，第二项则反过来，目前两项是$1:1$的权重求和，意味着两项相同程度地相互影响，而刚才我们说了，这辅助loss应该主要用来优化$e_k$而不是$z$，所以我们引入$\beta > \gamma > 0$，将辅助loss改为
\begin{equation}\beta\Vert e_k - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[e_k]\Vert^2\label{eq:ez2}\end{equation}
然后再加到重构loss中，就得到了VQ-VAE总的loss了

除此之外，$e_k$的优化还有另外的方案：首先将式$\eqref{eq:ez2}$的$\beta$置零，这样一来$e_k$就又没有梯度了；然后我们观察到，VQ-VAE的VQ操作其实跟K-Means聚类是有点相似的，$e_1,e_2,\cdots,e_K$相当于是$K$个聚类中心。根据我们对K-Means的了解，聚类中心等于该类的所有向量的平均，所以$e_k$的一种优化方案就是$z$的滑动平均
\begin{equation}e_k^{(t)} = \alpha e_k^{(t-1)} + (1-\alpha) z \end{equation}
这等价于指定使用SGD优化$\Vert e_k - \text{sg}[z]\Vert^2$这一项loss（其他项可以用Adam等）。该方案被VQ-VAE-2所使用。

FSQ #

可能有些读者疑惑，本文的主题不是FSQ吗？前面介绍VQ-VAE的篇幅是不是有点多了？事实上，由于FSQ完全对得起“简单得令人尴尬”这个评价，相比VQ-VAE，介绍FSQ只需要“寥寥几行”，所以VQ-VAE不写长点，这篇博客就没几个字了哈～当然，将VQ-VAE写详细一点，也能让大家更深刻体会到FSQ的简单。

准确来说，FSQ只是用来替代VQ-VAE中的“VQ”的，它的离散化思路非常非常简单，就是“四舍五入”。首先，假设我们有一个标量$t\in\mathbb{R}$，我们定义：
\begin{equation}\text{FSQ}(t)\triangleq \text{Round}[(L-1)\sigma(t)] \end{equation}
这里的$L\in\mathbb{N}$是一个超参数，$\sigma(x)=1/(1+e^{-x})$就是sigmoid函数（原论文用了$\tanh$，笔者认为用sigmoid更科学），$\text{Round}$就是四舍五入为一个整数，所以不难看出$\text{FSQ}(t)\in\{0,1,\cdots,L-1\}$，即FSQ运算将输出限制在了$L$个整数之中，从而实现了离散化。当然，多数情况下一个标量还不够，对于$z\in\mathbb{R}^d$，每一维可以执行FSQ运行，于是
\begin{equation}\text{FSQ}(z) = \text{Round}[(L-1)\sigma(z)]\in\{0,1,\cdots,L-1\}^d \end{equation}
即$d$维向量$z$被离散为$L^d$个整数之一。但要注意，$\text{Round}$操作同样是没有梯度的（或者说梯度为零），不过经过VQ-VAE的铺垫，有些读者可能已经猜到接下来要做什么了：同样是利用STE技巧
\begin{equation}\text{FSQ}(z) = (L-1)\sigma(z) + \text{sg}\big[\text{Round}[(L-1)\sigma(z)] - (L-1)\sigma(z)\big] \end{equation}
即反向传播用$\text{Round}$之前的$(L-1)\sigma(z)$求梯度。由于$\text{Round}$前后本身是数值近似的，所以FSQ不需要额外loss来迫使近似的出现，也没有额外的编码表需要更新，FSQ的简洁可见一斑！

实验 #

如果将VQ理解为直接将编码向量聚类为$K$个不同的类别，那么FSQ就是将编码向量归纳出$d$个属性，每个属性划分为了$L$个等级，从而直接表达了$L^d$个不同的整数。当然，从最一般的考虑，每个属性的等级数也可以是不相同的$L_1,L_2,\cdots,L_d$，从而不同的组合数为$L_1 L_2\cdots L_d$。

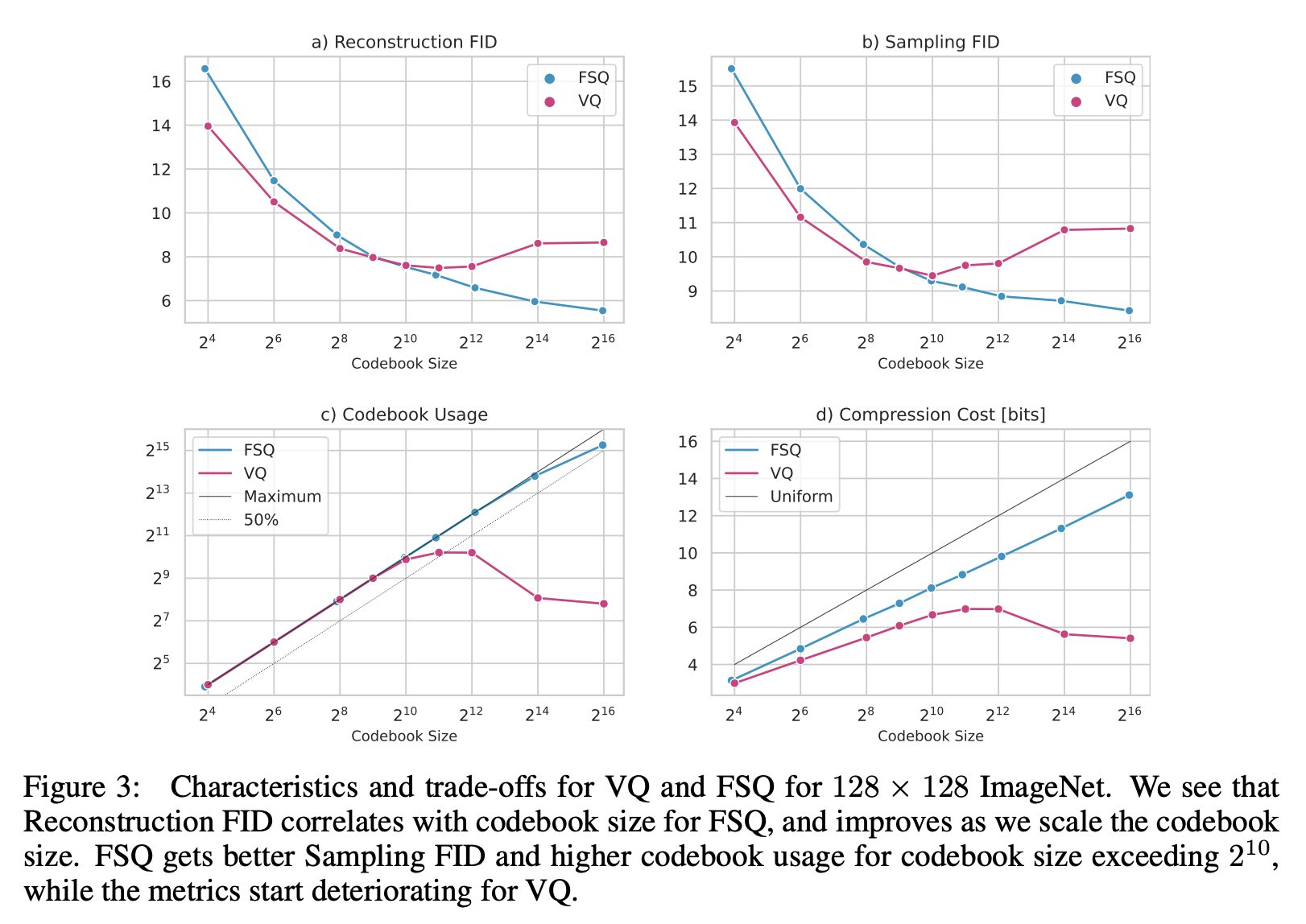
按照原论文的建议$L\geq 5$（之前的LFQ则相当于$L=2$），所以如果要对齐VQ-VAE的编码数量$K$的话，对于FSQ来说应该有$d = \log_L K$，即FSQ对编码向量的维度$d$是有限制的（一般就只是个位数），并且通常是远小于VQ-VAE的编码维度（一般是三位数），这个直接后果是当编码总数$K$比较小（从而$d$也比较小）时，FSQ的效果通常不如VQ：

从图上可以看到，当编码表大小在1000左右时，FSQ与VQ的效果接近；当编码表大小明显超过1000时，FSQ占优；反之当编码表大小明显小于1000时，则VQ占优，这跟笔者自己的实验结果相近。笔者的参考代码为：

Github: https://github.com/bojone/FSQ

其他实验就是比较常规的证明FSQ比VQ更优异的各种任务实验了，读者自行阅读原论文就好。

思考 #

从形式上来看，假设$K=L^d$，那么VQ就好比是“一个$L^d$类的分类器”，而FSQ则是“$d$个$L$级的打分器”，不管是从参数量、几何直观或者表达能力来看，其实FSQ都不如VQ，但为什么FSQ有机会取得比VQ更好的结果呢？笔者认为有两方面的原因。

第一个原因，是encoder和decoder太强。虽然FSQ本身弱一些，但是encoder和decoder都足够强了，所以基于神经网络的万能拟合能力假设，FSQ相对于VQ的劣势，完全可以在encoder和decoder中弥补过来。而在$K=L^d$的设定下，两者的离散化程度都是一样的，也就是说encoder与decoder之间的“信息瓶颈”是一样的，因此FSQ本身的问题就显得微不足道了。

第二个原因，是VQ的“队友”（梯度）太弱。VQ的经典问题是编码表坍缩：当编码表增大时，编码表并没有被充分利用起来，反而由于恶性竞争导致编码表聚集到一块了，经典表现就是一个5000的编码表，最终效果还不如500的编码表。归根结底，这是梯度不够合理所致，尽管VQ已经巧妙地设计了梯度，但对于$\mathop{\text{argmin}}$这种硬指派的运算，基于梯度的优化都存在“赢者通吃”问题，这是坍缩的根本原因，而FSQ的$\text{Round}$运算并不涉及到指派，它是直接取的近似值。当然，往大了讲，其实跟VQ类似的K-Means经常也有聚类中心坍缩的问题，可见$\mathop{\text{argmin}}$难优化已经是一个老大难的问题了。因此与其说FSQ太强，倒不如说是VQ的“队友”太弱。

从以上两点分析可以看出，FSQ要想超过VQ，除了编码表要足够大之外，还有encoder与decoder要足够复杂，但这并非总能满足，比如有些场景下，我们希望模型的每一层输出都被量化，这时候平摊下来的encoder和decoder未必足够复杂，此时FSQ本身的不足就成为效果的瓶颈了。此外，VQ之后的向量维度没有变化，可以是任意多维，而FSQ之前的向量必须投影到$d = \log_L K$维，这是很严重的降维，当我们需要用到投影之前的高维度近似向量时，就很难靠FSQ之后的低维向量简单恢复过来。

所以，如果单纯是作为“图像的Tokenzier”，那么FSQ或许已经可以取代VQ，但这并不意味着任意场景下VQ都可以被FSQ取代。

小结 #

本文介绍了VQ-VAE的“VQ”的一个及其简单的替代品——FSQ（Finite Scalar Quantization），它直接通过四舍五入来对连续向量进行离散化，并且不需要额外的loss进行辅助。实验结果表明，当编码表足够大时，FSQ比VQ更有优势。

转载到请包括本文地址：https://spaces.ac.cn/archives/9826

更详细的转载事宜请参考：《科学空间FAQ》