科学空间|Scientific Spaces

在此之前，BoJone的相册用的是phpyou相册程序，本来是喜欢它的简洁方便的，所以它这么多年不更新也没有介意。后来才发现，这个程序糟糕透了（不知道是不是我下载的版本不对）。昨天查了一下数据库，我发现我的数据库有16M大小，而一个phpyou就占用了12M，更离谱的是，它里边似乎镶嵌着许多不良敏感信息，所以，BoJone坚决抛弃它了。

现在使用的是kh_mod（中文网址），而它也是基于之前的MG2架设的，也是属于简洁相册的类型。新相册基本保留了原来的目录结构和图片。当然，之前的相册已经很久没有更新了，以后会多与大家分享一些瞬间的^_^

新相册

方轮自行车

你见过正方形轮子的自行车吗？一般认为，只有圆形的车轮才能使我们的车子平稳向前移动，但这只是针对平直道路而言的。谁规定路一定是平的？只要铺好一条适当的道路，正方形车轮的自行车照样可以平稳前行！本文就让我们为方轮自行车铺一条路。

其实，方轮自行车已经不是新鲜玩意了，它早已出现在不少科技馆中。从图片中可以看到，它的特殊轨道是有许多段弧组成的，每一段弧的长度等于正方形的边长。车轮前行时，正方形会保持与弧形相切（确保不会打滑）。这样的路的形状是什么曲线呢？很幸运，它并不十分复杂，而且让人意外的是，它就是我们之前已经研究过的“悬链线”！原来，要设计这样的一个曲线的轨道，不需要多么高深的设计师，只需要我们手拿一条铁链，让它自由垂下......

点击阅读全文...

计算机模拟的希格斯粒子（“上帝粒子”）衰变

笔者：对于科学界来说，七月份最重大的事情莫过于在LHC我们终于发现了希格斯玻色子的踪迹。BoJone到《新科学家》网站上选取了一篇文章进行翻译，让大家了解其中的一些事情。当然，发现这个希格斯玻色子已经是七月四号的事情了，现在已经是非常迟到了，中间的原因就是宇宙驿站的故障了......迟到总比没到好，现在发出来，与大家共勉。翻译得不好，请指出毛病，高手见笑了^_^

庆祝希格斯玻色子的最终发现！

作者：日内瓦的CERN 的Celeste Biever 2012年7月4日

点击阅读全文...

分类：千奇百怪,物理化学 标签：翻译, 模型, 粒子, 玻色子 阅读全文 3 评论

笔者这段时间对复数尤其感兴趣，当然，严格来讲应该是复变函数内容，其中一个原因是通过它，我们可以把一些看似毫不相关的内容联系了起来，体现了数学的简洁美和统一美。我相当有兴趣的其中一个内容是实分析中的泰勒级数和傅里叶级数。这两者都是关于某个函数的级数展开式，其中泰勒级数是用于一般函数展开的，其各项系数通过求n阶导数得到；傅里叶级数的对象是周期函数，其各项系数是通过定积分求得的。在实数世界里，两者毫不相关，但是，复分析却告诉我们：它们只是同一个东西！只是将其在不同的角度“投影”到实数世界里，就产生了不同的“物像”，以至于我们认为它们是不同东西而已。

我们直接来看一个变魔术般的运算：
我们知道，在实数世界里头，我们有
$ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+...$，其中$|x| < 1$

点击阅读全文...

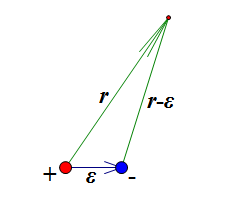
设想两个带有等量异号电荷的点电荷，它们之间的距离足够小，这样的一个模型被称为电偶极子（electric dipole）。我们研究电偶极子，主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述，比如一个小磁体周围的磁场，还有地球本身也可以近似看做一个偶极子来描述它的磁力情况，以及一些双原子分子的模型也被可以看做一个电偶极子模型，等等。在电偶极子模型中，两电荷的距离足够小，以至于我们忽略了一些关于距离的高次方项，只保留了线性部分，但对于物理探索来说，它已经足够精确，更重要的是，它足够简单，以至于我们可以容易把它清晰地描述出来。

我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q，两者距离为ε，根据库仑定律，一个点电荷产生的电势，正比于该电荷的电荷量，同时反比于到该点电荷的距离。那么，一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)

点击阅读全文...

上网的那些事儿

从申请帐号到接通校园网络，昨天晚上我总共花了将近3个小时才实现了在校内上网......

其实这本来不是一件很复杂的事情，但对于我的笔记本就是挺麻烦的。首先是申请，向隔壁师兄咨询了网管所在后，几分钟就申请到了账号，然后回到宿舍配置电脑。按照说明，是需要安装一个锐捷客户端的，通过手机把笔记本连上网络后，花了差不多20M流量下载了这个客户端，然后发现它竟然不能在Windows 8 64bit上运行。这就头疼了，我的笔记本只有Windows8和ubuntu呀，总不能为了上网换回Windows 7吧？就这样在两个系统中来来回回弄了两个小时，期间尝试过用mentohust来替换它，但发现在Windows 8上还是很头疼地不行。最后只能通过兼容模式来解决：

右击“锐捷客户端”的安装程序——属性——兼容性——选择以Windows 7兼容模式
右击“锐捷客户端”的安装程序——以管理员身份运行——安装程序——重新启动
然后就可以启动锐捷客户端了。我们用的是4.31版本。

点击阅读全文...

军训是比较辛苦，可是总有一些无聊的时刻。比如我们每次集合后的第一件事基本上都是站军姿，少则五分钟，长则二三十分钟，在这段时间里，头脑总得找点东西想才行，不然一动不动的，非常难熬。我就是在军训那些无聊的时刻里通过想数学问题来度过的。比如一有空余时间，我的头脑就浮现着级数$\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{p}$、哥德巴赫猜想、稳定性问题啦等等，并不是说要做出什么大发现，只是为了渡过无聊时间，也是对自己的思维能力和想象能力的锻炼吧。

之前提到过，昨天我们的“格斗方阵”去大学城表演了。在去大学城的过程中，我的一位“战友”问了我一个这样的问题：

在一个相互握手的人群中，握手奇数次的人总是有偶数个。每两个人可以握多于一次的手

他还说这是爱因斯坦提问的。这可把我的兴致给调动起来了。（后来我在网上搜索，却发现不了这个问题跟爱因斯坦的任何联系...）下边是我的颇有戏剧性的思考过程。

人群的握手问题

点击阅读全文...

其实很早之前我就想学习一款数学软件的使用，以前很感兴趣的是mathematica，也玩弄过一阵子，但毕竟在高中没有多大需要，也就没有坚持下来。更重要的是，这些软件都是要收费的。上了大学后，听了师兄姐对数学建模的讲述，发现他们基本上也是用mathematica或者matlab的，但这两个软件都是要收费的，我不大想用破解版本。既然我都已经用上了ubuntu了，那么我就该好好利用它。据说命令跟matlab很相似的软件是scilab，还有octave，不同的是这些都是开源免费的。

出于熟悉代码操作和数学软件编程的目的，我选择了学习scilab。虽然网上说octave与matlab的相似程度更高，但是我感觉scilab比octave用的更广一些，所以就用它。所谓“一理通百理明”，先专心学好一个。

下面是我编写的第一个scialb程序，利用威尔逊方法来进行素性测试。这个代码的主要目的是练习条件语句和循环语句，以及一些输出输入的技巧而已。程序本身比较丑陋。

//我的第一个scilab程序
//完成于2012.09.27

label1=['p:';];  //定义标签
B=x_mdialog(['本程序使用威尔逊方法判断进行素数测试。';'请输入要判断的数'],label1,['127';]);  //输入框
p=evstr(B(1));  //提取输入框里边的数字进行赋值
i=1;
j=1;
q=p-1;
while i<q
    j=j*i;
    j=modulo(j,p);//这个是模函数。
    i=i+1;
end
if j==1
    messagebox(['这是一个素数';],['测试结果']);  //输出，其中后边的“测试结果”是输入框的标题
else
    messagebox(['这是一个合数';],['测试结果']);
end

点击阅读全文...