费曼积分法——积分符号内取微分(1)
By 苏剑林 | 2012-06-10 | 78615位读者 | 引用椭圆内的一根定长弦(化圆法)
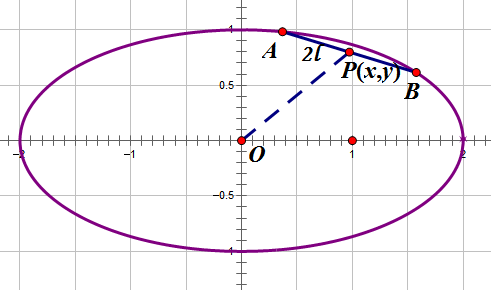
By 苏剑林 | 2012-07-06 | 30694位读者 | 引用在上一篇文章《抛物线内的一根定长弦》中,我们解决了抛物线内的定长弦中点轨迹问题,那还算是一个比较简单的问题。虽然同是圆锥曲线,但把同样的问题延伸到椭圆上,却不是那么简单了。因为椭圆的轨迹方程的x,y坐标通过平方相互“纠缠”在一起,不像抛物线方程那样可以容易分离开来(指的是分离成$y=f(x)$的形式)。BoJone尝试了若干种方法,还是难以把它的轨迹求出来。最后通过“化圆法”,终得轨迹方程。
所谓化圆法,就是将椭圆通过拉伸变成一个圆,利用圆的性质来解决一些问题。众所周知,相比椭圆,圆具有相当多的简单性。这是我高考前研究各种各样的高考圆锥曲线题时,所总结出来的一种方法。有时候,把椭圆拉伸为圆后,结论就相当显然了;同时,圆作为一个特殊的椭圆,椭圆的一般结论,放在圆上自然也是成立的。所以要研究椭圆问题,不妨先研究它的特例——圆问题;另一方面,利用圆的对称性等等,也可以大幅度地减少计算量,所以BoJone很喜欢这个方法。更想不到的是,它居然在求本文的轨迹时派上用场了。
“未解之谜”:为何不讲中点矩形法则?
By 苏剑林 | 2012-07-20 | 53522位读者 | 引用前言
在之前的一些文章中,我们已经指出过现行教材的一些毛病。比如主次不当(最明显的是那些一上来就讲线性方程组的线性代数教程)、缺乏直观性、缺少引导性等,我想其中最主要的原因可能是过于随大流了,别人怎么编我们也跟着怎么编,缺乏自己的观点和逻辑,因此导致一些常见的毛病就一直流传了下来。也许正因如此,就导致了有那么一种奇怪的现象——明明有一种计算量少的、精确度高一些的方法,教科书几乎从未提及;另外一种计算量稍大、精确度稍低的方法,但每一本同类教科书都讲述了它。不能不说这是一个“未解之谜”......
本文要讲的就是这样的两种方法,它们分别是用来求定积分近似值的“中点矩形法则”和“梯形法则”。对于后者我想绝大多数学习过微积分的朋友都会有印象,它就是那个几乎出现在了所有微积分教材的方法;而前者我相信不少读者都未曾听闻,但让人意外的是,它的计算量稍低,精确度却稍高。本文就简单介绍这两种方法,并且比较它们的精度。而本文的独特之处在于,证明过程沿用了《复分析:可视化方法》的思路,使用几何方法漂亮地估计误差!
我们的目标是在难以精确计算的情况下,通过一定的方法求出$\int_a^b f(x)dx$的近似值,这些方法基本上都是利用了积分即面积的思想。
两种不同的方法
高考早已成为了历史,报考、录取等也已经成为了过去,由于高考发挥不大好,所以最终我进了华南师范大学的数学勷勤创新班,在石牌校区(华师本部)的数学科学院。
有人曾问我考得这样的成绩遗憾吗?我说的确会有些遗憾,毕竟当初很有大志地冲着更加名牌的大学;不过要是问我后不后悔这样过了高三,我会坚决地说绝不后悔,而且我会非常高兴我是这样过了。(备考、研究、玩闹......)不管怎样,我会好好把握在大学的日子,专心研究,细细品味。我不相信一个大学就可以决定我的人生,但我肯定我的大学将会是我人生中重要的一部分。
要问我未来的计划,我只能说没有什么计划。是呀,未来这么远,这么“混沌”,怎么可能预测的了呢?不过还是可以“定性”地估计一下大概方向的,以后就想做研究型的工作,虽然学习的是数学,但还是努力将其结合物理一起来学吧。所以以后可能从事物理或数学相关工作,当然,要是这些都实现不了的话,我还可以去当一个老师,毕竟,教育也是我挺有兴趣的领域(尤其是看了宝莱坞的《三个傻瓜》之后)。如果自己不是人才,就希望能够培养一些人才出来^_^。
军训结束了,基本在华师安家了
By 苏剑林 | 2012-09-21 | 17224位读者 | 引用上网的那些事儿
从申请帐号到接通校园网络,昨天晚上我总共花了将近3个小时才实现了在校内上网......
其实这本来不是一件很复杂的事情,但对于我的笔记本就是挺麻烦的。首先是申请,向隔壁师兄咨询了网管所在后,几分钟就申请到了账号,然后回到宿舍配置电脑。按照说明,是需要安装一个锐捷客户端的,通过手机把笔记本连上网络后,花了差不多20M流量下载了这个客户端,然后发现它竟然不能在Windows 8 64bit上运行。这就头疼了,我的笔记本只有Windows8和ubuntu呀,总不能为了上网换回Windows 7吧?就这样在两个系统中来来回回弄了两个小时,期间尝试过用mentohust来替换它,但发现在Windows 8上还是很头疼地不行。最后只能通过兼容模式来解决:
右击“锐捷客户端”的安装程序——属性——兼容性——选择以Windows 7兼容模式
右击“锐捷客户端”的安装程序——以管理员身份运行——安装程序——重新启动
然后就可以启动锐捷客户端了。我们用的是4.31版本。
在上一篇文章中,我们已经得到了电偶极子的等势面和电场线方程,这应该可以让我们对电偶极子的力场情况有个大致的了解了。当然,我们还是希望能够求出在这样的一个受力情况下,一个带电粒子是如何运动的。简单起见,在下面的探讨中,我们假定带电粒子的质量和电荷量均为1,至于电荷的正负,可以通过改变在$U=-\frac{k \cos\theta}{r^2}$中的k值的正负来控制。我们使用的工具依旧是理论力学中的欧拉-拉格朗日方程。
也许不少读者始终对公式感到头疼,更不用说是博大精深的理论力学了。但是请相信我,如果你花一点点心思去弄懂用变分法研究力学(或其他物理系统,但我目前只会用于力学)的基本思路和步骤,那么对你的物理研究是大有裨益的。因为在我眼中,学习了一丁点的理论力学知识后,我看到的只有物理的简洁与和谐。有兴趣的朋友可以看看我的那几篇《自然极值》等相关文章。
首先写出动能的表达式:$T=\frac{1}{2} (\dot{r}^2+r^2 \dot{\theta}^2)$
还有势能:$U=-\frac{k \cos\theta}{r^2}$
高斯说过“数学是科学的皇后,而算术则是数学的女王。”这里的“算术”,其实就是我们现在所说的数论。从很小的时候开始,我便对数论情有独钟。虽然后来接触了很多更为有趣的数学分支,但是对数学的热情依然不减。我想,这大概是因为小时候的情结吧。小学时候,小小年纪的我,刚刚学完素数、合数、约数、整除等等概念,对数字尤其有兴趣。我想,在那时候我唯一能够读懂的数学难题只有数论这一领域吧。比如费马大定理,$x^n+y^n=z^n$,对于n大于2没有正整数解,很容易就知道它在讲什么;再比如,哥德巴赫猜想,每个大于4的偶数都可以分拆成两个奇素数之和,也很简单就弄懂它讲的是什么。所以,小小的我看懂了这些问题后就饶有兴致地摆弄数字啦,也许正因为如此,才让我对数字乃至对数学都有深厚的爱。
哥德巴赫猜想,无疑是数论中的一个璀璨明珠,可是目前来讲,它还是可望不可即的。一个看似如此简单的猜想,却困惑了数学家几百年,至今无人能解。尽管如此,我还是愿意细细地研究它,慢慢地品味它,在“论证”、或者说验算它的时候,欣赏到数学那神秘的美妙。本文主要就是研究给定偶数的“哥德巴赫分拆数”,即通过实际验算得出每个偶数分拆为两个素数之和的不同分拆方式的数目,比如6=3+3,只有一种分拆方式;8=3+5=5+3;有两种分拆方式;10=3+7=5+5=7+3,有三种分拆方式;等等。偶数2n的分拆数记为$G_2 (2n)$。
(这里定义的“分拆数”跟网上以及一般文献中的定义不同,这里把3+5和5+3看成是两种分拆方式,而网上一般的定义是只看成一种。我这里的定义的好处在于分拆方式的数目实际表示了分拆中涉及到的所有素数的个数。)
哥德巴赫猜想很难,这话没错,但是事实上哥德巴赫猜想是一个非常弱的命题。它说“每个大于4的偶数至少可以分拆成两个奇素数之和”,用上面的术语来说,就是每个偶数的“哥德巴赫分拆数”大于或等于1。可是经过实际验算发现,偶数越大,它的哥德巴赫分拆数越大,两者整体上是呈正相关关系的,比如$G_2 (100)=12,G_2 (1000)=56,G_2 (10000)=254$......所以,从强弱程度上来讲,这和“少于n的素数至少有一个”是差不多的(当然,难度有天壤之别)。
相对论和量子力学的初探
By 苏剑林 | 2012-10-16 | 33733位读者 | 引用=====大学学习=====
上大学已经一个多月了,除去军训的两周和国庆放假的一周,到现在已经是第三周上课了。我是数学专业的,由于是那个勷勤创新班,它希望我们都向研究型数学的方向发展,所以给我们“更多的自由研究时间”,所以课程比一般的班还少一点。由于高中已经对高等数学有个大概的了解,所以一开始让很多同学都喊苦的数学分析、解析几何于我而言都还是比较容易接受的。但从另外一个角度上来讲,我感觉我学得快的原因,倒不全是以前的积累,而是因为个人的学习方式。我不喜欢跟着老师的步伐走,我喜欢而且需要深入地思考和理解一个问题,希冀达到一理通百理明的效果,而不是做完一题紧接着下一题。因为我认为这种竞赛式的学习不能给我们带来实质性的进步,而且有可能抹杀了我们的创造力。
没有应用的数学是很枯燥乏味的,数学不能脱离物理、化学等领域。当然“应用”这个词有很广泛的意思,它不一定在实际生活中起到了立竿见影的作用,而是所有在非数学领域中体现了数学之美的例子都可以叫做数学应用,或者有趣的数学。所以,在经历了一两周纯粹地研究数学之后,我感觉我不能再这样下去了,与其零散地涉猎各个方面的知识,倒不如现在开始就系统地学习一些学科以外的科学知识。于是,我决定重拾高中还没有完成的事情——学习相对论和量子力学——所谓现代物理的两大支柱。











最近评论