科学空间|Scientific Spaces

词向量，英文名叫Word Embedding，按照字面意思，应该是词嵌入。说到词向量，不少读者应该会立马想到Google出品的Word2Vec，大牌效应就是不一样。另外，用Keras之类的框架还有一个Embedding层，也说是将词ID映射为向量。由于先入为主的意识，大家可能就会将词向量跟Word2Vec等同起来，而反过来问“Embedding是哪种词向量？”这类问题，尤其是对于初学者来说，应该是很混淆的。事实上，哪怕对于老手，也不一定能够很好地说清楚。

这一切，还得从one hot说起...

五十步笑百步

one hot，中文可以翻译为“独热”，是最原始的用来表示字、词的方式。为了简单，本文以字为例，词也是类似的。假如词表中有“科、学、空、间、不、错”六个字，one hot就是给这六个字分别用一个0-1编码：
$$\begin{array}{c|c}\hline\text{科} & [1, 0, 0, 0, 0, 0]\\
\text{学} & [0, 1, 0, 0, 0, 0]\\
\text{空} & [0, 0, 1, 0, 0, 0]\\
\text{间} & [0, 0, 0, 1, 0, 0]\\
\text{不} & [0, 0, 0, 0, 1, 0]\\
\text{错} & [0, 0, 0, 0, 0, 1]\\
\hline
\end{array}$$

点击阅读全文...

2016年即将画上句号了，在此祝各位读者2017年快乐，新的一年事事大顺哈～

happy new year 2017

所谓新年新气象，科学空间也换上新外衣。咦，怎么感觉没什么变化？别急，请继续看下去。

点击阅读全文...

中文语料库中，质量高而又容易获取的语料库，应该就是维基百科的中文语料了，而且维基百科相当厚道，每个月都把所有条目都打包一次（下载地址在这里：https://dumps.wikimedia.org/zhwiki/），供全世界使用，这才是真正的“取之于民，回馈于民”呀。遗憾的是，由于天朝的无理封锁，中文维基百科的条目到目前只有91万多条，而百度百科、互动百科都有千万条了（英文维基百科也有上千万了）。尽管如此，这并没有阻挡中文维基百科成为几乎是最高质量的中文语料库。（百度百科、互动百科它们只能自己用爬虫爬取，而且不少记录质量相当差，几乎都是互相复制甚至抄袭。）

门槛

尽量下载很容易，但是使用维基百科语料还是有一定门槛的。直接下载下来的维基百科语料是一个带有诸多html和markdown标记的文本压缩包，基本不能直接使用。幸好，已经有热心的高手为我们写好了处理工具，主要有两个：1、Wikipedia Extractor；2、gensim的wikicorpus库。它们都是基于python的。

然而，这两个主流的处理方法都不能让我满意。首先，Wikipedia Extractor提取出来的结果，会去掉{{}}标记的内容，这样会导致下面的情形

西方语言中“数学”（；）一词源自于古希腊语的（）

点击阅读全文...

这个系列慢慢写到第7篇，基本上也把分词的各种模型理清楚了，除了一些细微的调整（比如最后的分类器换成CRF）外，剩下的就看怎么玩了。基本上来说，要速度，就用基于词典的分词，要较好地解决组合歧义何和新词识别，则用复杂模型，比如之前介绍的LSTM、FCN都可以。但问题是，用深度学习训练分词器，需要标注语料，这费时费力，仅有的公开的几个标注语料，又不可能赶得上时效，比如，几乎没有哪几个公开的分词系统能够正确切分出“扫描二维码，关注微信号”来。

本文就是做了这样的一个实验，仅用一个词典，就完成了一个深度学习分词器的训练，居然效果还不错！这种方案可以称得上是半监督的，甚至是无监督的。

点击阅读全文...

魏尔斯特拉斯定理

将狄拉克函数理解为函数的极限，可以衍生出很丰富的内容，而且这些内容离严格的证明并不遥远。比如，定义
$$\delta_n(x)=\left\{\begin{aligned}&\frac{(1-x^2)^n}{I_n},x\in[-1,1]\\
&0,\text{其它情形}\end{aligned}\right.$$
其中$I_n = \int_{-1}^1 (1-x^2)^n dx$，于是不难证明
$$\delta(x)=\lim_{n\to\infty}\delta_n(x)$$
这样，对于$[a,b]$上的连续函数$f(x)$，我们就得到
$$f(x)=\int_{-1}^1 f(y)\delta(x-y)dy = \lim_{n\to\infty}\int_{-1}^1 f(y)\delta_n(x-y) dy$$
这里$-1 < a < b < 1$，并且我们已经“不严谨”地交换了积分号和极限号，但这不是特别重要。重要的是它的结果：可以看到
$$P_n(x)=\int_{-1}^1 f(y)\delta_n(x-y) dy$$
是$x$的一个$2n$次多项式，因此上式表明$f(x)$是一个$2n$次的多项式的极限！这就引出了著名的“魏尔斯特拉斯定理”：

闭区间上的连续函数都可以用多项式一致地逼近。

点击阅读全文...

咋看上去，SVD分解是比较传统的数据挖掘手段，自编码器是深度学习中一个比较“先进”的概念，应该没啥交集才对。而本文则要说，如果不考虑激活函数，那么两者将是等价的。进一步的思考就可以发现，不管是SVD还是自编码器，我们降维，并不是纯粹地为了减少储存量或者减少计算量，而是“智能”的初步体现。

等价性

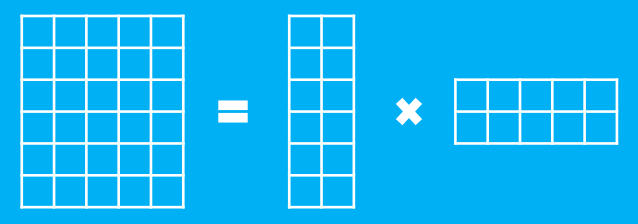
假设有一个$m$行$n$列的庞大矩阵$M_{m\times n}$，这可能使得计算甚至存储上都成问题，于是考虑一个分解，希望找到矩阵$A_{m\times k}$和$B_{k\times n}$，使得
$$M_{m\times n}=A_{m\times k}\times B_{k\times n}$$
这里的乘法是矩阵乘法。如图

SVD

点击阅读全文...

提前祝各位读者新年快乐，2017行好运～

这篇文章主要想回答两个“为什么”的问题：1、为啥我就对SVD感兴趣了？；2、为啥我说SVD是一个聚类过程？回答的内容纯粹个人思辨结果，暂无参考文献。

为什么要研究SVD？

从2015年接触深度学习到现在，已经研究了快两年的深度学习了，现在深度学习、数据科学等概念也遍地开花。为什么在深度学习火起来的时候，我反而要回去研究“古老”的SVD分解呢？我觉得，SVD作为一个矩阵分解算法，它的价值不仅仅体现在它广泛的应用，它背后还有更加深刻的内涵，即它的可解释性。在深度学习流行的今天，不少人还是觉得深度学习（神经网络）就是一个有效的“黑箱”模型。但是，仅用“黑箱”二字来解释深度学习的有效性显然不能让人满意。前面已经说过，SVD分解本质上与不带激活函数的三层自编码机等价，理解SVD分解，能够为神经网络模型寻求一个合理的概率解释。

点击阅读全文...

过程

在Python中，如果要多进程运算，一般是通过multiprocessing来实现的，常用的是multiprocessing中的进程池，比如：

from multiprocessing import Pool
import time

def f(x):
    time.sleep(1)
    print x+1
    return x+1

a = range(10)
pool = Pool(4)
b = pool.map(f, a)
pool.close()
pool.join()

print b

这样写简明清晰，确实方便，有趣的是，只需要将multiprocessing换成multiprocessing.dummy，就可以将程序从多进程改为多线程了。

点击阅读全文...