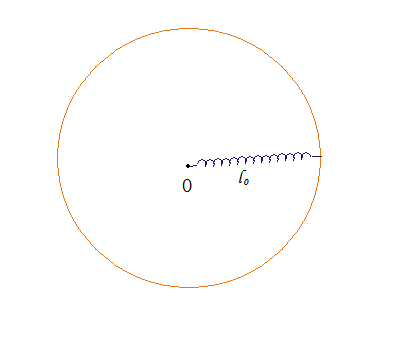
旋转的弹簧将如何伸长?
By 苏剑林 | 2010-07-30 | 95408位读者 | 引用【科学松鼠会】猫江湖(科学也是可以很有趣的)
By 苏剑林 | 2010-08-02 | 18369位读者 | 引用不要认为科学是一门多么枯燥、深奥的的学科,只要有点创意,科学也可以有趣起来。这种创意并非来源于专业人员,而是来源于生活,来源于关注 ,来源于一颗好奇而勇敢的心。下面请看科学松鼠会推出的《猫江湖》。
我有一个梦想,这个种群将会觉醒,实现其立群信条的真谛:猫猫生而平等;
我有一个梦想,在食堂垃圾桶边,阉割猫和健全公猫能同席而坐,共叙兄弟情谊;
我有一个梦想,甚至连临时喂食点这个正义匿迹、压迫成风的地方,也将变成平等和自由的绿洲;
我有一个梦想,让天下的猫孩儿都有爸爸,我的四个孩子将在一个不是以他们的毛色,而是以健康优劣作为评判标准的国家里生活;
科学空间:2010年8月重要天象
By 苏剑林 | 2010-08-02 | 25839位读者 | 引用三次方程的三角函数解法
By 苏剑林 | 2010-08-08 | 83859位读者 | 引用对于解方程,代数学家希望能够从理论上证明解的存在性以及解的求法,所以就有了1到4次方程的求根公式、5次及以上的代数方程没有根式可解等重要理论;然而,通常的学者(如物理学家、天文学家)都不需要这些内容,他们只关心如何尽可能快地求出指定方程的根(尤其是实数根),所以他们通常关注的是方程的数值算法,当然,如果能有一个相对简单的求根公式,也是他们所希望的。而接下来所要介绍的内容,则是满足了这一需要的三次方程的求根公式,其中用到的相当一部分的理论,是与三角函数相关的。
储备
\begin{equation}\frac{2}{\tan 2A}=\frac{1}{\tan A}-\tan A\end{equation}
\begin{equation}\frac{2}{\sin 2A}=\frac{1}{\tan A}+\tan A\end{equation}
\begin{equation}\cos(3A)=4\cos^3 A-3\cos A\end{equation}
旋转的弹簧将如何伸长(2)?
By 苏剑林 | 2010-08-07 | 27579位读者 | 引用《方程与宇宙》:拉格朗日点的点点滴滴(四)
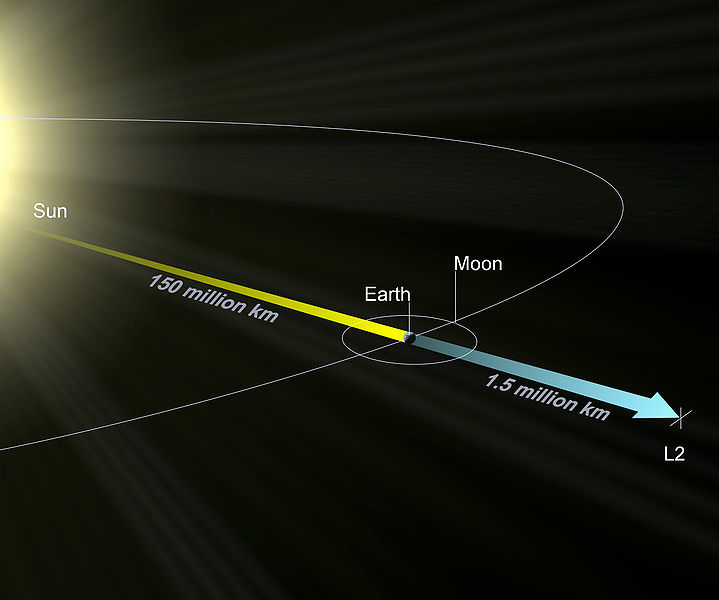
By 苏剑林 | 2010-08-15 | 91612位读者 | 引用The New Calculation Of Lagrangian Point 1,2,3
关于n体问题,选择质心或其他定点为参考点,我们可以列出下面的运动方程:
$$\ddot{\vec{r}}_k=\sum_{i=1,i != k}^{n} Gm_i\frac{\vec{r}_i-\vec{r}_k}{|\vec{r}_i-\vec{r}_k|^3}\tag{19}$$
现在我们只考虑三体问题。天文学家一直希望能够找到三体问题的简洁解,可是很遗憾,庞加莱已经证明了三体问题的解是混沌的,也就是说任何微小的扰动都有可能造成不可预料的后果(可以形象的比喻为:巴西的一只蝴蝶翅膀的扇动,有可能因此美国的一场龙卷风)。
《方程与宇宙》:拉格朗日点,复数,向量(五)
By 苏剑林 | 2010-08-16 | 51031位读者 | 引用The New Calculation Of Lagrangian Point 4,5
上一回我们已经求出了拉格朗日点L1,L2,L3,并且希望能够求出L4,L5两个点。由于L4,L5与“地球-太阳”连线已经不共线了,所以前边的方法貌似不能够用了。为了得到一个通用的定义,我们可以采用以下方法来描述拉格朗日点:位于拉格朗日点的天体,它与太阳的连线以及地球与太阳的连线所组成的角的大小是恒定的。(这里为了方便,采用了地日系的拉格朗日点来描述,对于一般的三体问题是一样的)
对于L4,L5来说,我们或许可以设置一个新的向量来描述这两点的向径(如$\vec{R}$)。当我们这样做后,很快就会发现这样会令我们的计算走向死胡同。因为我们发现:已知两个向量的夹角和其中一个向量,我们很难把另一个向量用已知向量的式子表达出来。不能做到这一点,就不能找出$\vec{R}$与$\vec{r}$的关系,就无法联立方程求解。难道,我们这一条路走到尽头了吗?一开始BoJone也冥思苦想不得头绪,但是...
与向量的渊源极深的四元数
By 苏剑林 | 2010-08-27 | 32265位读者 | 引用当我们在使用向量进行几何、物理研究的时候,是否曾经想到:向量竟然起源于“数”?
当向量还没有发展起来的时候(虽然“有方向有大小的量”很早就被人们认识),复数已经得到了认可并且有了初步应用。当我们把复数跟向量联系起来时,我们也许会认为,因为复平面表示的复数运算与向量有着相似之处,才把复数跟几何联系起来。然而事实却相反,向量是从对复数乃至一种称为“四元数”的东西的研究中逐渐分离出来的。换句话说,历史中出现过“四元数”与向量分别研究几何的阶段,麦克斯韦(Maxwell) 将四元 数的数量部分和矢量部分分开,作为 实 体处理,作了大量的矢量分析。三维矢量分析的建立,及同四元数的正式分裂是18世纪80年代由Gibbs和Heaviside独立完成的。矢量代数被推广到矢量函数和矢量微积分,由此开始了四元数和矢量分析的争论,最终矢量分析占了上风。因而“四元数”渐渐离开了教科书。不过,“四元数”的一些特殊而巧妙的应用,仍然使我们不至于忘记它。











最近评论