Transformer升级之路:7、长度外推性与局部注意力
By 苏剑林 | 2023-01-12 | 85658位读者 | 引用对于Transformer模型来说,其长度的外推性是我们一直在追求的良好性质,它是指我们在短序列上训练的模型,能否不用微调地用到长序列上并依然保持不错的效果。之所以追求长度外推性,一方面是理论的完备性,觉得这是一个理想模型应当具备的性质,另一方面也是训练的实用性,允许我们以较低成本(在较短序列上)训练出一个长序列可用的模型。
下面我们来分析一下加强Transformer长度外推性的关键思路,并由此给出一个“超强基线”方案,然后我们带着这个“超强基线”来分析一些相关的研究工作。
思维误区
第一篇明确研究Transformer长度外推性的工作应该是ALIBI,出自2021年中期,距今也不算太久。为什么这么晚(相比Transformer首次发表的2017年)才有人专门做这个课题呢?估计是因为我们长期以来,都想当然地认为Transformer的长度外推性是位置编码的问题,找到更好的位置编码就行了。
Transformer升级之路:12、无限外推的ReRoPE?
By 苏剑林 | 2023-08-07 | 60885位读者 | 引用自从在《Transformer升级之路:11、将β进制位置进行到底》中引入混合进制的思路进一步推广了NTK-aware Scaled RoPE后,笔者感觉类似思路的效果已经达到了上限,想要更大幅度的提升就必须另辟蹊径了。这时候笔者想起了此前构思过的一个思路,该思路由于复杂度较高所以被搁置下了,既然现在已经遇到了瓶颈,那么“唯一的办法就是最好的办法”,于是便将它重拾起来。
万万没想到的是,尽管该方法增加了一些推理复杂度,但它的实验效果却惊人地好——甚至隐约有无限的长度外推能力!因此,笔者迫不及待地撰写了本文来分享该方法。由于形式上跟ReLU激活函数的相似性,所以笔者将该方法命名为“ReRoPE (Rectified Rotary Position Embeddings)”。
重温
我们知道,RoPE形式上是一种绝对位置编码,但实际上给Attention带来的是相对位置信息,即如下的Toeplitz矩阵:
Google新作试图“复活”RNN:RNN能否再次辉煌?
By 苏剑林 | 2023-03-28 | 56546位读者 | 引用当前,像ChatGPT之类的LLM可谓是“风靡全球”。有读者留意到,几乎所有LLM都还是用最初的Multi-Head Scaled-Dot Attention,近年来大量的Efficient工作如线性Attention、FLASH等均未被采用。是它们版本效果太差,还是根本没有必要考虑效率?其实答案笔者在《线性Transformer应该不是你要等的那个模型》已经分析过了,只有序列长度明显超过hidden size时,标准Attention才呈现出二次复杂度,在此之前它还是接近线性的,它的速度比很多Efficient改进都快,而像GPT3用到了上万的hidden size,这意味着只要你的LLM不是面向数万长度的文本生成,那么用Efficient改进是没有必要的,很多时候速度没提上去,效果还降低了。
那么,真有数万甚至数十万长度的序列处理需求时,我们又该用什么模型呢?近日,Google的一篇论文《Resurrecting Recurrent Neural Networks for Long Sequences》重新优化了RNN模型,特别指出了RNN在处理超长序列场景下的优势。那么,RNN能否再次辉煌?
【个人翻译】变暖的地球对冷血动物来说过热?
By 苏剑林 | 2009-07-08 | 32480位读者 | 引用行动起来!共同应对全球气候变暖
By 苏剑林 | 2009-08-29 | 16161位读者 | 引用8月28日是距离哥本哈根气候大会召开倒数100天的日子。
在这个特殊的日子,绿色和平将以特别的行动,邀请了广大的中国公众一起关注全球变暖,参与拯救气候的伟大使命。
11点至16点这五个小时内,“我在乎”和观众们一起来观看见证了这些“冰孩子”们的命运:
中国 — 8月28日,无数双眼睛见证了这样的一幕:绿色和平取自长江、黄河和恒河三条大江源头的冰川融水在北京制作而成冰雕孩子,同印度新德里雕刻成数字“100”的冰雕遥相呼应。冰小孩的在北京和印度新德里的迅速“消失”,告诉我们喜马拉雅—青藏高原地区冰川的加速消融,影响最大的当然是亚洲国家人民的生活。
证明光速不变的一个理想实验??
By 苏剑林 | 2012-10-18 | 62680位读者 | 引用在狭义相对论发表之前和之后,都有不少实验从不同角度论证了它的正确性。这些实验大多数是实际测量得出结果的,当然也存在着一些“理想实验”,这些实验只需要一定的逻辑推理,而实际上是无法完成的。下面就是我很久之前在某本书(很抱歉,我真的忘记书名了)看到的一个用来推翻光速可叠加的伽利略变换的理想实验。它只用寥寥几句,就好像已经证明了“c+c=c”(c是真空中的光速)的事实。可是“c+c=c”在狭义相对论上是作为原理出现的,是不可能通过逻辑推理来证明的。事实究竟如何?我们先来看这个实验。
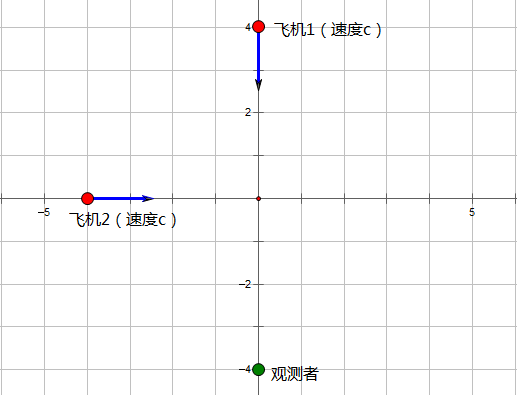
任意选定一个坐标原点。设想原点的正北方$c\cdot t_0$处有一架以光速$c$朝南运行的飞机1;原点的正西方$c\cdot t_0$处有一架以光速$c$朝东运行的飞机2。假设就这样匀速运动着,显然,$t_0$时间后,将会发生惨剧(飞机相撞)。
熵不变性Softmax的一个快速推导
By 苏剑林 | 2022-04-11 | 18149位读者 | 引用在文章《从熵不变性看Attention的Scale操作》中,我们推导了一版具有熵不变性质的注意力机制:
\begin{equation}Attention(Q,K,V) = softmax\left(\frac{\kappa \log n}{d}QK^{\top}\right)V\label{eq:a}\end{equation}
可以观察到,它主要是往Softmax里边引入了长度相关的缩放因子$\log n$来实现的。原来的推导比较繁琐,并且做了较多的假设,不利于直观理解,本文为其补充一个相对简明快速的推导。
推导过程
我们可以抛开注意力机制的背景,直接设有$s_1,s_2,\cdots,s_n\in\mathbb{R}$,定义
$$p_i = \frac{e^{\lambda s_i}}{\sum\limits_{i=1}^n e^{\lambda s_i}}$$
分享:孟岩的《理解矩阵》一文
By 苏剑林 | 2012-10-22 | 57724位读者 | 引用之前已经提到我要自学相对论和量子力学。作为现代物理的两大支柱,所用的数学也是很“现代”的,不能总是用高中那套简单的模式来计算,所以线性代数是我要熟悉的一门课程之一。现在大一还没开设线性代数课程,但是我所持的观点是:“任何东西只要你需要它,你就应该去学,而且能够学会。”其实我初三暑假的时候就开始接触了线性代数,我看的那本教材,跟国内其他线性代数教材一样,采用了一种只要求记忆和计算的方式来教授,先讲从线性方程组引出行列式,再到矩阵。我那时也在背诵,知道了了行列式怎么算的,行列式可以用来解方程组,矩阵是怎么相乘的等等。但我完全不知道为什么,我甚至不懂为什么这门课程叫“线性代数”。(当然,也有可能是那时的数学水平不够)国外很多教程都讲的很好,很规范地教,但是对于国内像我这样平庸的学生又显得过于专业。我一直期待有这样的一个平衡点,可惜一直没有找到,所以只能从各种渠道摸索。










最近评论