设想两个带有等量异号电荷的点电荷,它们之间的距离足够小,这样的一个模型被称为电偶极子(electric dipole)。我们研究电偶极子,主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述,比如一个小磁体周围的磁场,还有地球本身也可以近似看做一个偶极子来描述它的磁力情况,以及一些双原子分子的模型也被可以看做一个电偶极子模型,等等。在电偶极子模型中,两电荷的距离足够小,以至于我们忽略了一些关于距离的高次方项,只保留了线性部分,但对于物理探索来说,它已经足够精确,更重要的是,它足够简单,以至于我们可以容易把它清晰地描述出来。
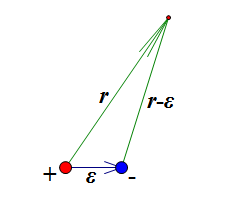
我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q,两者距离为ε,根据库仑定律,一个点电荷产生的电势,正比于该电荷的电荷量,同时反比于到该点电荷的距离。那么,一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)
军训结束了,基本在华师安家了
By 苏剑林 | 2012-09-21 | 17241位读者 | 引用上网的那些事儿
从申请帐号到接通校园网络,昨天晚上我总共花了将近3个小时才实现了在校内上网......
其实这本来不是一件很复杂的事情,但对于我的笔记本就是挺麻烦的。首先是申请,向隔壁师兄咨询了网管所在后,几分钟就申请到了账号,然后回到宿舍配置电脑。按照说明,是需要安装一个锐捷客户端的,通过手机把笔记本连上网络后,花了差不多20M流量下载了这个客户端,然后发现它竟然不能在Windows 8 64bit上运行。这就头疼了,我的笔记本只有Windows8和ubuntu呀,总不能为了上网换回Windows 7吧?就这样在两个系统中来来回回弄了两个小时,期间尝试过用mentohust来替换它,但发现在Windows 8上还是很头疼地不行。最后只能通过兼容模式来解决:
右击“锐捷客户端”的安装程序——属性——兼容性——选择以Windows 7兼容模式
右击“锐捷客户端”的安装程序——以管理员身份运行——安装程序——重新启动
然后就可以启动锐捷客户端了。我们用的是4.31版本。
又折腾网络了......
By 苏剑林 | 2012-09-25 | 24794位读者 | 引用今晚主要干了两件事情:
1、实现了在windows 8的情况下,把自己的笔记本当做wifi的信号发射点,共享校园网(即“笔记本 wifi 热点”那技术,不知道这样会不会折损电脑寿命呀)。主要方法如下:
1.1、安装.net 3.5,安装方法:
挂载windows 8的安装光盘,
然后右击开始菜单(Win + X)的左下角,选择-命令提示符(管理员),接着然后输入如下命令:
dism.exe /online /enable-feature /featurename:NetFX3 /Source:F:\sources\sxs
其中F是安装光盘的驱动器符号。接下来是漫长等待,估计会有十多分钟,就会提示安装进度100%了。
1.2、安装Connectify软件,直接到官网下载最新的精简版就行,有兴趣可以购买专业版。安装后需要重新启动,然后简单地配置一下就行了,不再细说。
附:
顺便提一下,我也试过国内的wifi共享精灵,但是发现它会卡在“查找当前配置信息”那里,这折腾了我几个小时,最终还是没有解决...所以还是用回外国软件了。
均值不等式的两个巧妙证明
By 苏剑林 | 2012-09-26 | 52693位读者 | 引用记得几年前,BoJone提供过一个证明均值不等式(代数—几何平均不等式)的方法,但是其中的证明有点长,有点让人眼花缭乱的感觉(虽然里边的思想还是挺简单的)。昨天在上《数学分析》课程的时候,老师讲到了这个不等式,也讲了他的证明,用的是数学归纳法,感觉还是没有那种简洁美和巧妙美。但这让我回想起了之前我研究过的两种巧妙证明方法,可是在昨天划了一整天,都没有把这两种方法回忆起来。直到今天才回想起来,所以就放在这里与大家分享,同时也作备忘之用。
对于若干个非负数$x_i$,我们有
$$\frac{x_1+x_2+...+x_n}{n} \geq \sqrt[n]{x_1 x_2 ... x_n}$$
记为$A_n \geq G_n$
证明1:数学归纳法
这个方法不算简单,但是非常巧妙,它从n递推到n+1的过程让人拍案叫绝。用数学归纳法证明詹森不等式也是同样的递推思路,而均值不等式不过是詹森不等式的一个特例而已。
假设$A_n \geq G_n$成立,要证$A_{n+1} \geq G_{n+1}$。我们有
$$\begin{aligned}&2n A_{n+1}=(n+1)A_{n+1}+(n-1)A_{n+1} \\
=&[x_1 + x_2 +...+x_n]+[x_{n+1}+(n-1)A_{n+1}] \\
\geq &nG_n+n(x_{n+1}\cdot A_{n+1}^{n-1})^{\frac{1}{n}} \\
\geq &2n(G_{n+1}^{n+1}\cdot A_{n+1}^{n-1})^{\frac{1}{2n}}\end{aligned}$$
《新理解矩阵1》:矩阵是什么?
By 苏剑林 | 2012-10-29 | 74646位读者 | 引用前边我承诺过会写一些关于自己对矩阵的理解。其实孟岩在《理解矩阵》这三篇文章中,已经用一种很直观的方法告诉了我们有关矩阵以及线性代数的一些性质和思想。而我对矩阵的理解,大多数也是来源于他的文章。当然,为了更好地理解线性代数,我还阅读了很多相关书籍,以求得到一种符合直觉的理解方式。孟岩的blog已经很久没有更新了,在此谨引用他的标题,来叙述我对矩阵的理解。
当然,我不打算追求那些空间、算子那些高抽象性的问题,我只是想发表一下自己对线性代数中一些常用工具的看法,比如说矩阵、行列式等。同时,文章命名为“理解矩阵”,也就是说这不是矩阵入门教程,而是与已经有一定的线性代数基础的读者一起探讨关于矩阵的其他理解方式,仅此而已。我估计基本上学过线性代数的读者都能够读懂这篇文章。
首先,我们不禁要追溯一个本源问题:矩阵是什么?
王骁威:勇敢的追梦者
By 苏剑林 | 2012-11-06 | 40496位读者 | 引用破解数学猜想
今天在看《广州日报》时,偶然发现了一个不曾听闻的名字——王骁威。
他,跟我一样是一个90后,是韶关学院的大四学生,而现在,他多了一点名头:“仅用1表示数问题中的素数猜想”这一难题的破解者。
“仅用1表示数问题中的素数猜想”出现在加拿大数学家Richard K·Guy的著作《数论中未解决的问题》中,是上世纪50年代,加拿大数学家Richard K·Guy提出一个数论猜想:对于给定的素数p,$f(p)=f(p-1)+1$是否能成立。其中,“仅用1表示数”指的是只用1通过加法和乘法以及括号来表示自然数,对于给定的自然数n,用1来表示时,1的最少个数记为$f(n)$。据说在之前就有诸多数学家论证过,在3亿之前的素数里,上述猜想是成立的。
但是王骁威通过举出反例证否了这个命题,他指出p=353942783时这个公式并不成立。他是经过四个月的钻研,王骁威运用集合论的运算、分析、优化,才成功发现这个猜想的反例的。发现反例之后,王骁威陷入兴奋,把整理成的报告寄给国内几家杂志社,结果却令他失望,几家杂志社对他的论文均不感兴趣。“我也怀疑过自己的努力是否值得,但对数学的强烈兴趣让我坚持下来。”王骁威说自己将论文译成英文,英文名为《A counterexample to the prime conjecture of expressing numbers using just ones》(中文名为《仅用1表示数中素数猜想的一个反例》),投往全球最权威的数论杂志———美国艾斯维尔出版社的《Journal of Number Theory》(数论杂志),国外专家的青睐终于让他收获成功的喜悦,论文发表在杂志第133期(明年二月)上。数学大师丘成桐也通过邮件与王骁威交流,并对他表示肯定。
Astronomy Calendar of Celestial Events
2012年全年天象
翻译自NASA:http://eclipse.gsfc.nasa.gov/SKYCAL/SKYCAL.html
(北京时间)
一月
01 日 14:15 上弦月
01 日 金星位于: 34° E
03 二 04:19 月球过远地点: 404600 km
04 三 15:23 象限仪座流星雨:ZHR = 120
05 四 11:59 地球过近日点:0.9833 AU
05 四 17:17 月合昴宿星团 3.1° N
06 五 22:30 月亮过升交点
07 六 05:46 月亮过最北点: 22.5° N
09 一 15:30 满月
16 一 15:21 月合角宿一 2° N
16 一 17:08 下弦月
18 三 05:28 月球过近地点: 369900 km
20 五 02:26 月亮过降交点
20 五 10:12 月亮过最南点: 22.5° S
23 一 15:39 新月
31 二 01:42 月球过远地点:404300 km
31 二 12:10 上弦月









最近评论