【理解黎曼几何】5. 黎曼曲率

现在我们来关注黎曼曲率。总的来说，黎曼曲率提供了一种方案，让身处空间内部的人也能计算自身所处空间的弯曲程度。俗话说，“不识庐山真面目，只缘身在此山中”，还有“当局者迷，旁观者清”，等等，因此，能够身处空间之中而发现空间中的弯曲与否，是一件很了不起的事情，就好像我们已经超越了我们现有的空间，到了更高维的空间去“居高临下”那样。真可谓“心有多远，路就有多远，世界就有多远”。

如果站在更高维空间的角度看，就容易发现空间的弯曲。比如弯曲空间中有一条测地线，从更高维的空间看，它就是一条曲线，可以计算曲率等，但是在原来的空间看，它就是直的，测地线就是直线概念的一般化，因此不可能通过这种途径发现空间的弯曲性，必须有一些迂回的途径。可能一下子不容易想到，但是各种途径都殊途同归后，就感觉它是显然的了。

怎么更好地导出黎曼曲率来，使得它能够明显地反映出弯曲空间跟平直空间的本质区别呢？为此笔者思考了很长时间，看了不少参考书（《引力与时空》、《场论》、《引力论》等），比较了几种导出黎曼曲率的方式，简要叙述如下。

求导顺序不能乱了 #

一般的张量分析或者黎曼几何教材中，导出黎曼曲率的方式是考虑二阶协变导数顺序的差别：
$$A^{\mu}_{;\alpha;\beta}-A^{\mu}_{;\beta;\alpha}=-R^{\mu}_{\nu\alpha\beta}A^{\nu} \tag{40} $$
由此可以分离出黎曼曲率张量$R^{\mu}_{\nu\alpha\beta}$来，这确实是一种爽快的途径，但它的几何意义并不明显，很难看出它是怎么反映空间是曲还是直的。而且我们现在还没有定义二阶协变导数（一次协变导数后有两个指标，即相当于一个矩阵而不是向量了，定义高阶协变导数需要细节上的跟进），而这个定义基本上是纯粹代数演算，目前对我们来说意义不大，因此我们这里不作定义，读者直接参考教材即可，所以我们也不对这种方案多作讨论。

在弯曲空间邂逅 #

此外，还有通过测地线偏离（在广义相对论中对应于潮汐力）来导出黎曼曲率的，那也算是一种几何意义和物理意义都很明确的方案，但是涉及到的计算比较繁琐。主要思路是：考虑测地线方程
$$\frac{d^2 x^{\mu} }{ds^2}+\Gamma_{\alpha\beta}^{\mu}(x) \frac{d x^{\alpha} }{ds}\frac{d x^{\beta} }{ds}=0 \tag{41} $$
假设有另一条测地线$x(s)+\delta x(s)$，那么它满足方程
$$\frac{d^2 (x^{\mu} + \delta x^{\mu}) }{ds^2}+\Gamma_{\alpha\beta}^{\mu}(x+\delta x) \frac{d (x^{\alpha}+\delta x^{\alpha}) }{ds}\frac{d (x^{\beta}+\delta x^{\beta}) }{ds}=0 \tag{42} $$
假设$\delta x$和$d\delta x/ds$都是无穷小量，两式作差，得到
$$\frac{d^2 \delta x^{\mu}}{ds^2}+\frac{\partial \Gamma_{\alpha\beta}^{\mu}}{\partial x^{\nu}}\delta x^{\nu} \frac{d x^{\alpha} }{ds}\frac{d x^{\beta}}{ds}+2\Gamma_{\alpha\beta}^{\mu}\frac{d \delta x^{\alpha} }{ds}\frac{d x^{\beta}}{ds}=0 \tag{43} $$
其中$\delta x$就被称为测地线偏离，在黎曼几何中，称之为“雅可比向量场”。上述形式已经足够简单，然而，我们倾向于写成协变导数的形式，因为协变导数才是在弯曲空间中合理的导数，前面我们已经定义了沿测地线的导数$\frac{DA^{\mu}}{Ds}$，重复一次，我们就能够得到沿测地线的二阶导数$\frac{D^2 A^{\mu}}{Ds^2}=\frac{D}{Ds}\left(\frac{DA^{\mu}}{Ds}\right)$，这是容易办到的，但因为我们这里不是特别关心这种方案，因此就不写出$\frac{D^2 A^{\mu}}{Ds^2}$的具体形式了，读者可以自己推导。经过计算后，就会发现
$$\frac{D^2 \delta x^{\mu}}{Ds^2}=-R^{\mu}_{\nu\alpha\beta}\delta x^{\alpha}\frac{dx^{\nu}}{ds}\frac{dx^{\beta}}{ds} \tag{44} $$
这就出现了曲率张量$R^{\mu}_{\nu\alpha\beta}$。从数学来看，非零的$R^{\mu}_{\nu\alpha\beta}$实际上表明了测地线分布的不均匀，这就是弯曲空间的体现之一。

这种方案让笔者想起了几米的漫画作品《向左走·向右走》，说的是男女主角一个习惯向左走，一个习惯向右走，于是他们两个看起来永远不会相遇。但有一天他们在圆形喷水池相遇了——在圆的一端背向行走，最终在圆的另一端相遇了。而在弯曲空间中，比如在球面上，即便两条平行线也有相交的机会。这其实表明，“弯曲”其实更为深刻和有趣，它给予了我们世界更多的可能性。

“溜达”回来的变化 #

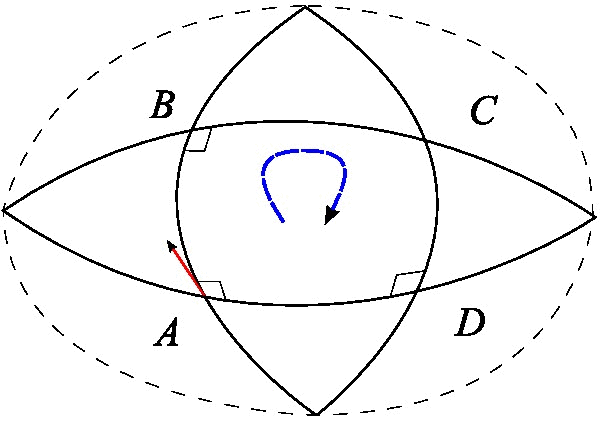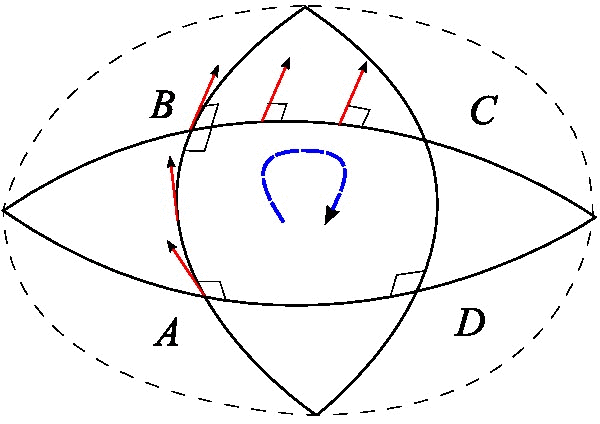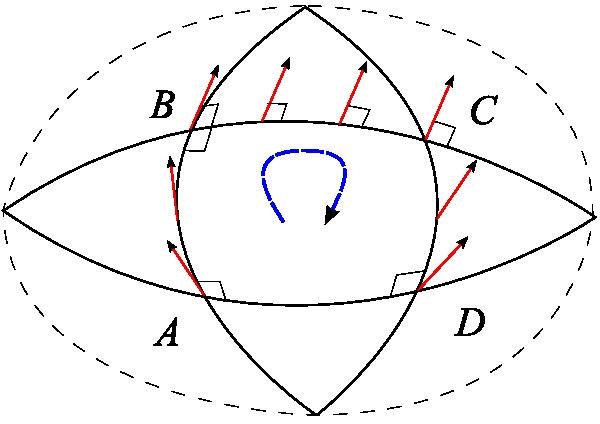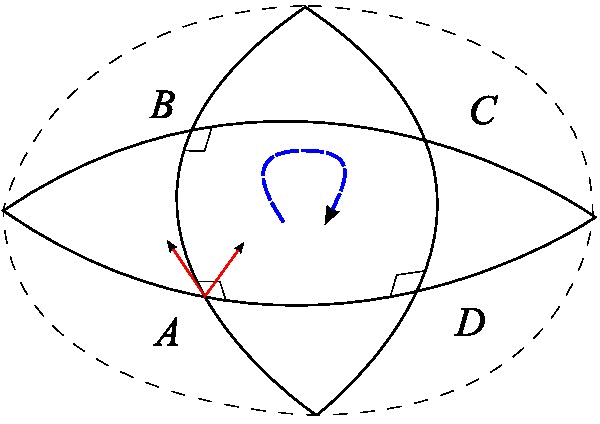
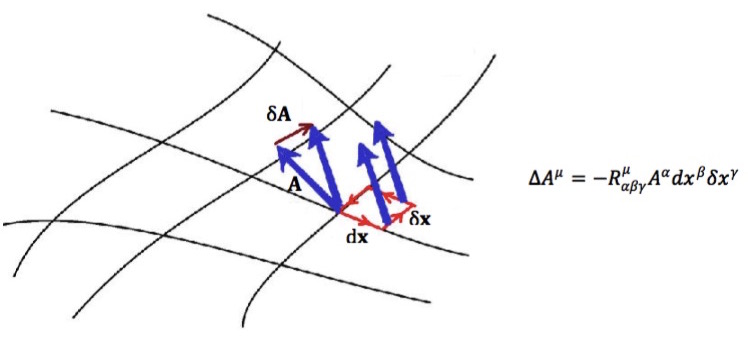
最后还有一种分析向量沿着闭合曲线平移后的变化的方案，我们在这里详细分析它。事实上它跟测地线偏离是等价的，只是它的几何意义更加明显，有助于导出更为深刻的结果。它表明，如果一个向量“溜达”一圈回来之后，它就不一定是原来的向量了。下图的例子就清晰表明了这一点。

假设$x^{\mu}$处有任意一个向量$A^{\mu}$，从$x^{\mu}$出发，先平移无穷小量$dx^{\mu}$，再平移无穷小量$\delta x^{\mu}$，然后再平移无穷小量$-dx^{\mu}$，最后平移无穷小量$-\delta x^{\mu}$，也就是沿着一个无穷小的平行四边形走了一圈，回到原点：
$$x^{\mu}\to x^{\mu}+dx^{\mu}\to x^{\mu}+dx^{\mu}+\delta x^{\mu}\to x^{\mu}+\delta x^{\mu}\to x^{\mu}$$

我们逐步计算平移过程中$A^{\mu}$的变化，从$x^{\mu}$到$x^{\mu}+dx^{\mu}$，$A^{\mu}$变为
$$A^{\mu}-\Gamma^{\mu}_{\alpha\beta}(x) A^{\alpha}dx^{\beta} \tag{45} $$
接着从$x^{\mu}+dx^{\mu}$到$x^{\mu}+dx^{\mu}+\delta x^{\mu}$，$A^{\mu}$变为
$$\begin{aligned}&A^{\mu}-\Gamma^{\mu}_{\alpha\beta}(x) A^{\alpha}dx^{\beta}-\Gamma^{\mu}_{\nu\gamma}(x+dx) \left[A^{\nu}-\Gamma^{\nu}_{\alpha\beta}(x) A^{\alpha}dx^{\beta}\right]\delta x^{\gamma}\\
=&A^{\mu}-\Gamma^{\mu}_{\alpha\beta}(x) A^{\alpha}dx^{\beta}-\Gamma^{\mu}_{\nu\gamma}(x) A^{\nu} \delta x^{\gamma} \\
&\quad- \frac{\partial \Gamma^{\mu}_{\nu\gamma}(x)}{\partial x^{\beta}} A^{\nu} dx^{\beta} \delta x^{\gamma} + \Gamma^{\mu}_{\nu\gamma}(x) \Gamma^{\nu}_{\alpha\beta}(x) A^{\alpha} dx^{\beta}\delta x^{\gamma}
\end{aligned} \tag{46} $$
这里我们只精确到二阶项。

类似地，如果考虑路径$x^{\mu}\to x^{\mu}+\delta x^{\mu}\to x^{\mu}+dx^{\mu}+\delta x^{\mu}$所带来的变化，则只需要将$dx$和$\delta x$交换
$$\begin{aligned}&A^{\mu}-\Gamma^{\mu}_{\alpha\beta}(x) A^{\alpha}\delta x^{\beta}-\Gamma^{\mu}_{\nu\gamma}(x) A^{\nu} d x^{\gamma} \\
&\quad- \frac{\partial \Gamma^{\mu}_{\nu\gamma}(x)}{\partial x^{\beta}} A^{\nu} \delta x^{\beta} d x^{\gamma} + \Gamma^{\mu}_{\nu\gamma}(x) \Gamma^{\nu}_{\alpha\beta}(x) A^{\alpha} \delta x^{\beta} d x^{\gamma}\end{aligned} \tag{47} $$
那么很自然地，路径$x^{\mu}+dx^{\mu}+\delta x^{\mu}\to x^{\mu}+\delta x^{\mu}\to x^{\mu}$所造成的变化就是上式的相反数。于是，整条闭合路径$x^{\mu}\to x^{\mu}+dx^{\mu}\to x^{\mu}+dx^{\mu}+\delta x^{\mu}\to x^{\mu}+\delta x^{\mu}\to x^{\mu}$所带来的变化就是两式之差。调整一下求和指标，然后作差，不难得到
$$\label{bihelujingbianhua}\begin{aligned}\Delta A^{\mu} =&-\left(\frac{\partial \Gamma^{\mu}_{\alpha\gamma}}{\partial x^{\beta}}-\frac{\partial \Gamma^{\mu}_{\alpha\beta}}{\partial x^{\gamma}}+\Gamma^{\mu}_{\nu\beta}\Gamma^{\nu}_{\alpha\gamma}-\Gamma^{\mu}_{\nu\gamma}\Gamma^{\nu}_{\alpha\beta}\right)A^{\alpha} dx^{\beta}\delta x^{\gamma}\\
=&-R^{\mu}_{\alpha\beta\gamma} A^{\alpha} dx^{\beta}\delta x^{\gamma}\end{aligned} \tag{48} $$
这里
$$R^{\mu}_{\alpha\beta\gamma}=\frac{\partial \Gamma^{\mu}_{\alpha\gamma}}{\partial x^{\beta}}-\frac{\partial \Gamma^{\mu}_{\alpha\beta}}{\partial x^{\gamma}}+\Gamma^{\mu}_{\nu\beta}\Gamma^{\nu}_{\alpha\gamma}-\Gamma^{\mu}_{\nu\gamma}\Gamma^{\nu}_{\alpha\beta} \tag{49} $$
就是黎曼曲率张量的定义式了，它有4个指标，是一个非常“宏伟”的量。

一句话来说 #

三种不同的黎曼曲率张量的导出方式，分别从三个角度表明了弯曲空间与平直空间的区别：平直空间中，协变导数的次序是可以交换的，弯曲空间则不是；平直空间中，测地线分布的均匀的、线性的，弯曲空间则不是；平直空间中，一个向量去“溜达”一圈回来之后，并没有变化，而弯曲空间中，向量去“溜达”完之后，可能就不是原来的向量了。

转载到请包括本文地址：https://spaces.ac.cn/archives/4014

更详细的转载事宜请参考：《科学空间FAQ》