科学空间|Scientific Spaces

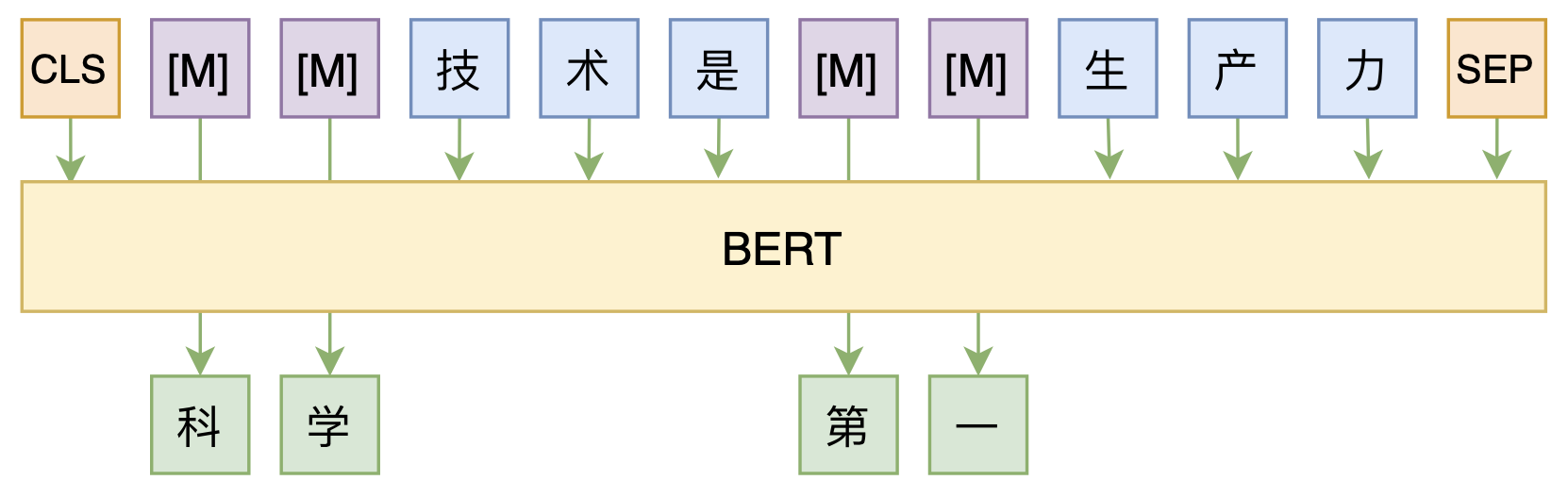
大家都知道，MLM（Masked Language Model）是BERT、RoBERTa的预训练方式，顾名思义，就是mask掉原始序列的一些token，然后让模型去预测这些被mask掉的token。随着研究的深入，大家发现MLM不单单可以作为预训练方式，还能有很丰富的应用价值，比如笔者之前就发现直接加载BERT的MLM权重就可以当作UniLM来做Seq2Seq任务（参考这里），又比如发表在ACL 2020的《Spelling Error Correction with Soft-Masked BERT》将MLM模型用于文本纠错。

MLM任务示意图

然而，仔细读过BERT的论文或者亲自尝试过的读者应该都知道，原始的MLM的训练效率是比较低的，因为每次只能mask掉一小部分的token来训练。ACL 2020的论文《Fast and Accurate Deep Bidirectional Language Representations for Unsupervised Learning》也思考了这个问题，并且提出了一种新的MLM模型设计，能够有更高的训练效率和更好的效果。

点击阅读全文...

随着NLP的发展，像Word2Vec、Glove这样的词向量模型，正逐渐地被基于Transformer的BERT等模型代替，不过经典始终是经典，词向量模型依然在不少场景发光发热，并且仍有不少值得我们去研究的地方。本文我们来关心一个词向量模型可能有的疑惑：词向量的维度大概多少才够？

先说结论，笔者给出的估算结果是
\begin{equation}n > 8.33\log N\label{eq:final}\end{equation}
更简约的话可以直接记$n > 8\log N$，其中$N$是词表大小，$n$就是词向量维度，$\log$是自然对数。当$n$超过这个阈值时，就说明模型有足够的容量容纳这$N$个词语（当然$n$越大过拟合风险也越大）。这样一来，当$N=100000$时，得到的$n$大约是96，所以对于10万个词的词向量模型来说，维度选择96就足够了；如果要容纳500万个词，那么$n$大概就是128。

点击阅读全文...

类别不平衡问题，也称为长尾分布问题，在本博客里已经有好几次相关讨论了，比如《从loss的硬截断、软化到focal loss》、《将“Softmax+交叉熵”推广到多标签分类问题》、《通过互信息思想来缓解类别不平衡问题》。对于缓解类别不平衡，比较基本的方法就是调节样本权重，看起来“高端”一点的方法则是各种魔改loss了（比如Focal Loss、Dice Loss、Logits Adjustment等），本文希望比较系统地理解一下它们之间的联系。

长尾分布：少数类别的样本数目非常多，多数类别的样本数目非常少。

从光滑准确率到交叉熵

这里的分析主要以sigmoid的2分类为主，但多数结论可以平行推广到softmax的多分类。设$x$为输入，$y\in\{0,1\}$为目标，$p_{\theta}(x) \in [0, 1]$为模型。理想情况下，当然是要评测什么指标，我们就去优化那个指标。对于分类问题来说，最朴素的指标当然就是准确率，但准确率并没有办法提供有效的梯度，所以不能直接来训练。

点击阅读全文...

深度学习如此成功的一个巨大原因就是基于梯度的优化算法（SGD、Adam等）能有效地求解大多数神经网络模型。然而，既然是基于梯度，那么就要求模型是可导的，但随着研究的深入，我们时常会有求解不可导模型的需求，典型的例子就是直接优化准确率、F1、BLEU等评测指标，或者在神经网络里边加入了不可导模块（比如“跳读”操作）。

Gradient

本文将简单介绍两种求解不可导的模型的有效方法：强化学习的重要方法之一策略梯度（Policy Gradient），以及干脆不需要梯度的零阶优化（Zeroth Order Optimization）。表面上来看，这是两种思路完全不一样的优化方法，但本文将进一步证明，在一大类优化问题中，其实两者基本上是等价的。

点击阅读全文...

在预训练语言模型中，ALBERT和ELECTRA算是继BERT之后的两个“后起之秀”。它们从不同的角度入手对BERT进行了改进，最终提升了效果（至少在不少公开评测数据集上是这样），因此也赢得了一定的口碑。但在平时的交流学习中，笔者发现不少朋友对这两个模型存在一些误解，以至于在使用过程中浪费了不必要的时间。在此，笔者试图对这两个模型的一些关键之处做下总结，供大家参考，希望大家能在使用这两个模型的时候少走一些弯路。

ALBERT与ELECTRA

（注：本文中的“BERT”一词既指开始发布的BERT模型，也指后来的改进版RoBERTa，我们可以将BERT理解为没充分训练的RoBERTa，将RoBERTa理解为更充分训练的BERT。本文主要指的是它跟ALBERT和ELECTRA的对比，因此不区分BERT和RoBERTa。）

点击阅读全文...

Teacher Forcing是Seq2Seq模型的经典训练方式，而Exposure Bias则是Teacher Forcing的经典缺陷，这对于搞文本生成的同学来说应该是耳熟能详的事实了。笔者之前也曾写过博文《Seq2Seq中Exposure Bias现象的浅析与对策》，初步地分析过Exposure Bias问题。

Teacher Forcing示意图

本文则介绍Google新提出的一种名为“TeaForN”的缓解Exposure Bias现象的方案，来自论文《TeaForN: Teacher-Forcing with N-grams》，它通过嵌套迭代的方式，让模型能提前预估到后$N$个token（而不仅仅是当前要预测的token），其处理思路上颇有可圈可点之处，值得我们学习。

（注：为了尽量跟本博客旧文章保持一致，本文的记号与原论文的记号有所不同，请大家以理解符号含义为主，不要强记符号形式。）

点击阅读全文...

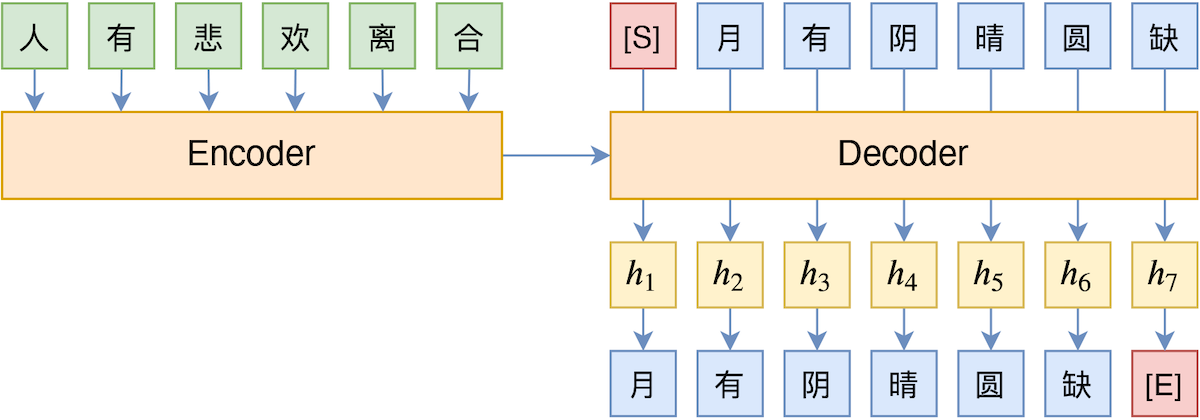
不知道大家对Google去年的屠榜之作T5还有没有印象？就是那个打着“万事皆可Seq2Seq”的旗号、最大搞了110亿参数、一举刷新了GLUE、SuperGLUE等多个NLP榜单的模型，而且过去一年了，T5仍然是SuperGLUE榜单上的第一，目前还稳妥地拉开着第二名2%的差距。然而，对于中文界的朋友来说，T5可能没有什么存在感，原因很简单：没有中文版T5可用。不过这个现状要改变了，因为Google最近放出了多国语言版的T5（mT5），里边当然是包含了中文语言。虽然不是纯正的中文版，但也能凑合着用一下。

“万事皆可Seq2Seq”的T5

本文将会对T5模型做一个简单的回顾与介绍，然后再介绍一下如何在bert4keras中调用mT5模型来做中文任务。作为一个原生的Seq2Seq预训练模型，mT5在文本生成任务上的表现还是相当不错的，非常值得一试。

点击阅读全文...

刚看到一个有意思的结论：

对于任意实数$x$及偶数$n$，总有$\sum\limits_{k=0}^n \frac{x^k}{k!} > 0$，即$e^x$在$x=0$处的偶次泰勒展开式总是正的。

下面我们来看一下这个结论的证明，以及它在寻找softmax替代品中的应用。

证明过程

看上去这是一个很强的结果，证明会不会很复杂？其实证明非常简单，记
\begin{equation}f_n(x) = \sum\limits_{k=0}^n \frac{x^k}{k!}\end{equation}
当$n$是偶数时，我们有$\lim\limits_{x\to\pm\infty} f_n(x)=+\infty$，即整体是开口向上的，所以我们只需要证明它的最小值大于0就行了，又因为它是一个光滑连续的多项式函数，所以最小值点必然是某个极小值点。那么换个角度想，我们只需要证明它所有的极值点（不管是极大还是极小）所对应的函数值都大于0。

点击阅读全文...