科学空间|Scientific Spaces

自由落体公式-示意图

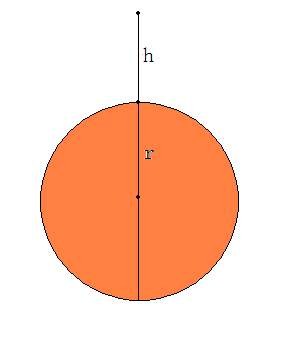
自由落体的一般定义是：只考虑吸引天体和被吸引天体的引力因素，忽略其他的运动和大气摩擦等因素，物体从静止（相对于吸引天体）开始接近吸引天体的运动。根据这个定义，假设地球为一个均匀球体，半径为r，质量为M，物体从距离地表h高度处自由落下。求落到地面的时间t，或者根据时间t求h。

令s为t时刻物体左右下落的物体与地表的距离，忽略物体的小质量，那么可以列出微分方程：
$$\frac{d^2 s}{dt^2}=-\frac{GM}{(r+s)^2}\tag{1}$$并且初始条件是$t=0,s=h,\dot{s}=v=0$

在实际应用中，我们不必求出这道微分方程的精确解，因为这个解极其麻烦，在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。

点击阅读全文...

gam2010-logo

“同是地球人，共享一片天”（One People, One Sky）

超越2009国际天文年，“2010全球天文月”应运而生。“全球天文月”希望号召全世界各地的人们参与到仰望星空的活动中来，创造更大的共享意识。正如口号说的那样——“同是地球人，共享一片天”（One People, One Sky）。北京天文馆在4月将组织一系列活动，欢迎您的参与。

点击阅读全文...

昨天在浏览网页的时候，发现了一道有趣的方程：
$$x^{x^{x^{\dots}}}=2$$
各位读者先别急着往下看，不妨自己求解一下？

点击阅读全文...

月掩金星-20100516

春夏之交的五月，天气逐渐热了起来。随着太阳直射点逐渐北移，对于我们来说，夜晚也将变得短暂。然而，这个月的精彩天象并未减少，金星的观测条件越来越好，而继上月水星东大距之后，5月下旬它还将运行到西大距的位置，月初宝瓶座η流星雨也将上演，天文爱好者又要忙活起来了。

点击阅读全文...

图片说明：火星上的沙尘暴，版权：Jean-Luc Dauvergne, Francois Colas, IMCCE/S2P, Obs. Midi-Pyrénées

点击阅读全文...

阅读小提示：亲爱的读者，你可以选择不读这篇文章，但如果你选择了阅读，请一定要阅读完。BoJone对“半途而废”所造成的后果一概不负责任^_^。

函数图像旋转

我们来考虑下一个旋转问题：将某一函数图像y=f(x)，绕点(p,q)逆时针旋转了θ角之后，得到的图象的解析式。

点击阅读全文...

图片说明：奋进号航天飞机夜晚发射，版权：NASA

点击阅读全文...

我要上学了

越来越佩服前人，说出了“光阴似箭，日月如梭”的真理。是呀，期末考试仿佛只是在昨天，今天已经又要上学了；俯仰之间，一个月的时间就过去了。

毫无疑问，又因为我的懒惰和不坚持，浪费了我很多的时间。回想一下寒假，我究竟收获了什么呢？主要是两个方面吧：学术和情感。

学术上，主要是数学和天文学里面的内容。数学我主要是深入了微积分方面的内容，把微积分的思想深刻了一点点，把微分方程（组）熟悉了一点点。我有一种很熟悉的感觉：现在自学高等数学，就好比我之前在小学时间学习中学数学。那时候超傻，书本上说了$\lim_{\Delta x->0} f'(x)=\frac{f(x+\Delta x)-f(x)}{\Delta x}$，我看不懂这个式子，整天郁闷$f(x)$是不是指$f\cdot (x)$。不过尽管那时候不懂这些，还是懂应用，我用导数最基本的定义去求极值，得出了一些有趣的发现，使我的兴趣倍增。现在学习微积分也是这样的感觉，我觉得我仅仅是很显浅地接触到，还有很多等待仔细琢磨....

点击阅读全文...