Ladder Side-Tuning:预训练模型的“过墙梯”
By 苏剑林 | 2022-06-20 | 103532位读者 |如果说大型的预训练模型是自然语言处理的“张良计”,那么对应的“过墙梯”是什么呢?笔者认为是高效地微调这些大模型到特定任务上的各种技巧。除了直接微调全部参数外,还有像Adapter、P-Tuning等很多参数高效的微调技巧,它们能够通过只微调很少的参数来达到接近全量参数微调的效果。然而,这些技巧通常只是“参数高效”而并非“训练高效”,因为它们依旧需要在整个模型中反向传播来获得少部分可训练参数的梯度,说白了,就是可训练的参数确实是少了很多,但是训练速度并没有明显提升。
最近的一篇论文《LST: Ladder Side-Tuning for Parameter and Memory Efficient Transfer Learning》则提出了一个新的名为“Ladder Side-Tuning(LST)”的训练技巧,它号称同时达到了参数高效和训练高效。是否真有这么理想的“过墙梯”?本来就让我们一起来学习一下。
方法大意 #
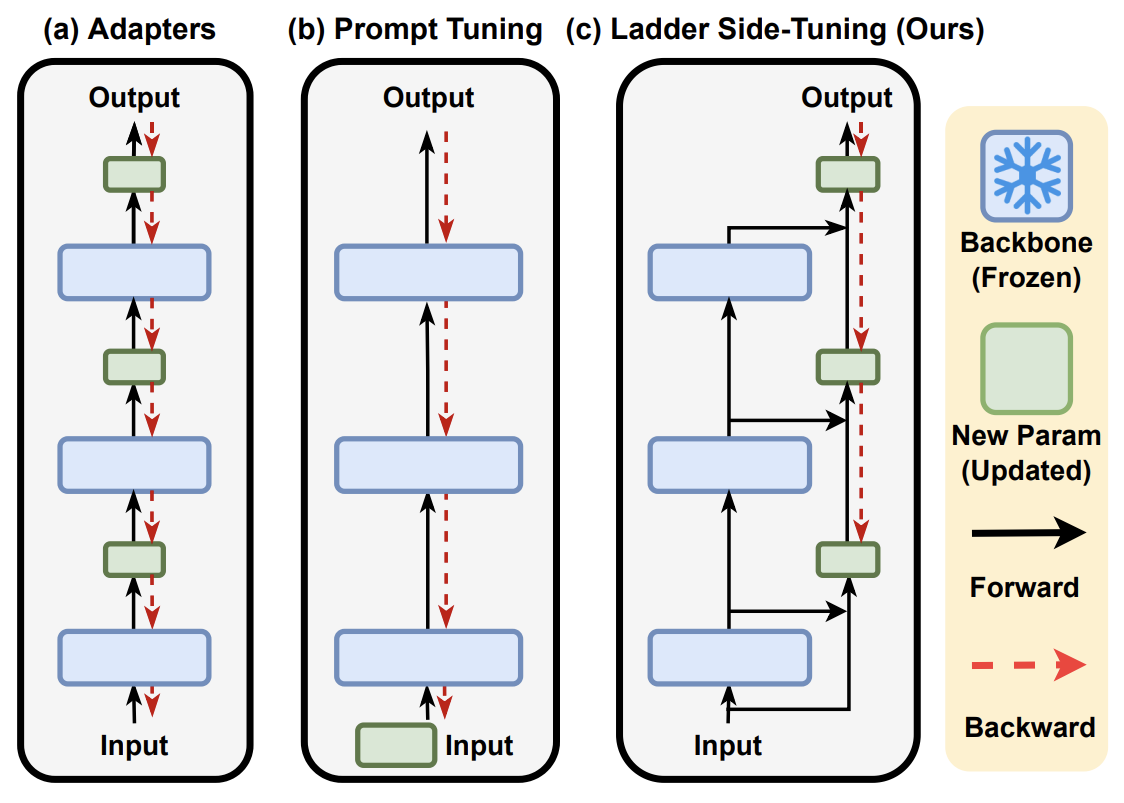
其实LST这把“过墙梯”的结构,用原论文的Figure 2就可以清晰地说清楚了:
反向传播,也就是求模型梯度,是从输出层向输入层逐步计算的,因此反向传播的深度/计算量,取决于最靠近输入层的参数深度,跟可训练的参数量没有太必然的联系。对于Adapter来说,它在每一层后面都插入了一个小规模的层,虽然其余参数都固定了,只有新插入的层可训练,但每一层都新层,所以反向传播要传到输入层;对于P-tuning来说,本质上它是只有在Embedding层中有少量可训练参数,但Embedding层是输入层,因此它的反向传播也要贯穿整个模型。因此,这两种方案能提升的训练效率并不多。
至于LST,它是在原有大模型的基础上搭建了一个“旁支”(梯子),将大模型的部分层输出作为旁枝模型的输入,所有的训练参数尽在旁枝模型中,由于大模型仅提供输入,因此反向传播的复杂度取决于旁枝模型的规模,并不需要直接在原始大模型上执行反向传播,因此是可以明显提升训练效率的。
实验效果 #
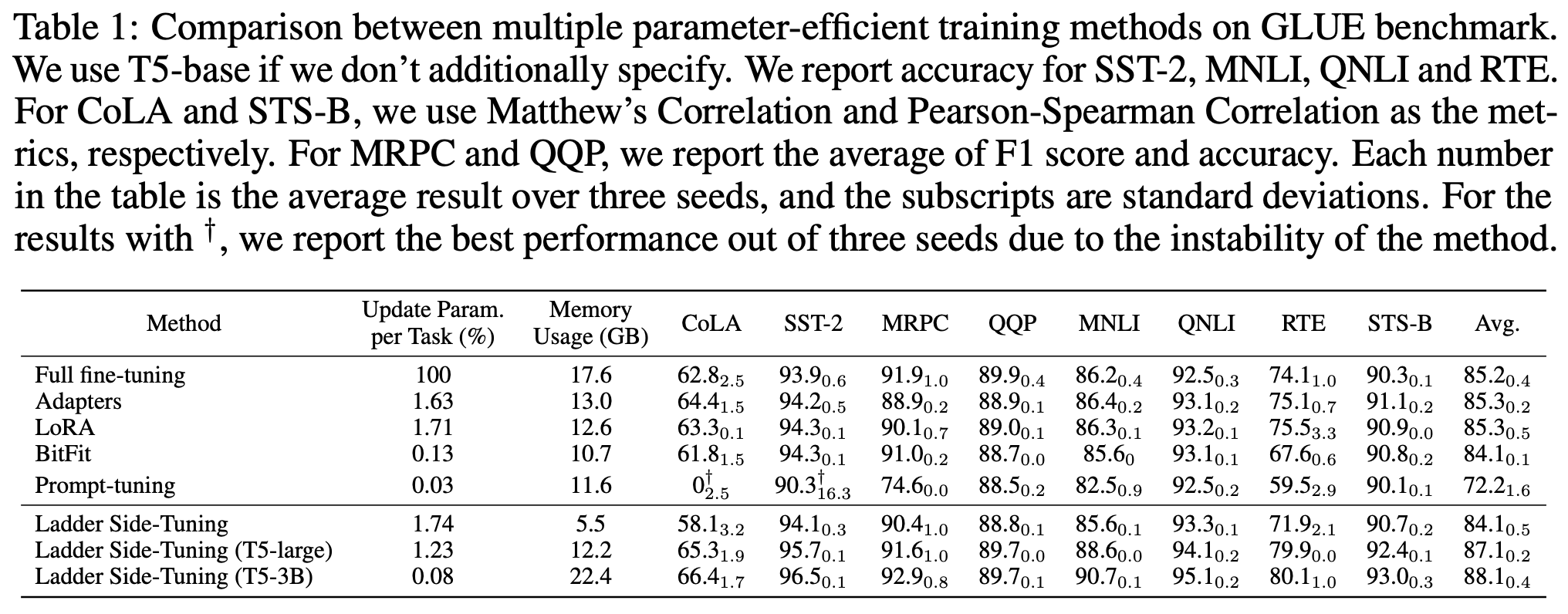
原论文做了不少LST的实验,包括NLP、CV的,下面是LST在GLUE数据集上的效果:
可以看到,LST确实具备了参数高效和训练高效的特点,能够在较小的训练参数和训练成本的情况下,达到一个不错的微调效果。特别是最后两行的实验结果,体现出了LST在有限训练资源下微调大模型的可能性。
笔者在中文的CLUE任务上也做了简单尝试,参考代码为:
注意,原论文的“梯子”是用跟Adapter中的MLP层来搭建的,而笔者上述实现直接用了Transformer一样的“Attention + FFN”组合,可训练的参数量控制在100万左右,约为base版的1.2%,或者large版的0.4%,梯子的初始化直接用随机初始化,最终在验证集的效果如下:
$$\small{\begin{array}{c|ccccccccccc}
\hline
& \text{iflytek} & \text{tnews} & \text{afqmc} & \text{cmnli} & \text{ocnli} & \text{wsc} & \text{csl} & \text{cmrc2018} & \text{c3} & \text{chid} & \text{cluener}\\
\hline
\text{BERT base} & 60.06 & 56.80 & 72.41 & 79.56 & 73.93 & 78.62 & 83.93 & 56.17 & 60.54 & 85.69 & 79.45 \\
\text{RoBERTa base} & 60.64 & 58.06 & 74.05 & 81.24 & 76.00 & 87.50 & 84.50 & 56.54 & 67.66 & 86.71 & 79.47\\
\hline
\text{RoBERTa base + LST} & 59.29 & 56.82 & 70.37 & 76.27 & 71.02 & 68.09 & 82.63 & 42.50 & 56.97 & 69.35 & 78.30\\
\text{RoBERTa large + LST} & 60.41 & 57.12 & 72.36 & 75.80 & 72.07 & 75.00 & 84.23 & 39.98 & 60.19 & 72.55 & 77.80\\
\hline
\end{array}}$$
可以看到,实验结果没有原论文的英文实验那么乐观(当然不排除是笔者自己的实现不够好),但训练效率确实有明显提升(平均来说提升一倍左右)。整个实验下来,笔者的感觉是对于比较常规、一般难度的分类任务,LST能取得相近的效果,但对于比较困难的任务,比如阅读理解等,LST会有非常明显的下降。
当然,其实应该不只是LST有这个问题,大部分号称参数高效的微调方法估计都有这个问题,因为这些方法的实验任务多数都只是GLUE,GLUE其实全都是相对简单的分类任务...
延伸思考 #
从“事后诸葛亮”来看,其实LST也算不上多高明的做法,本质上就是把预训练模型固定住,然后把其输出层和部分中间层的结果作为补充输入来训练一个新的小模型,理解到这一点之后,想必很多读者已经在脑海中酝酿着自己的相似方案了。不过,LST真正的意义在于告诉我们可以这样做,并且给出了一个可行的参考方案,以及实验证明了它确实是大模型的一个有效利用方案。
有类似研究经验的读者会发现,LST新增的“梯子”分支的初始化是个问题,如果完全随机初始化的话,可能会有训练上的困难,效果效果会不理想。这一点原论文也提到了,它提供了一个截取大模型矩阵权重来作为小模型矩阵初始化的方案,从而提升了LST的最终效果,其细节可以在论文中找到,至于笔记自己的实现,就纯粹是简单验证LST的有效性,所以就偷懒没实现这一步。
进一步想,既然LST新增的“梯子”分支存在初始化难题,而LST确实是微调大模型的有效方案,那么未来我们在训练新的大模型时,是不是就可以事先把这个“梯子”也预留好呢?也就是说,我们直接把这个“梯子”作为预训练模型的一部分做大规模的预训练,后面微调的时候,就只微调“梯子”,这样就可以实现高效地微调大模型,又不用担心初始化问题?
从形式上来看,笔者觉得LST跟《BERT-of-Theseus:基于模块替换的模型压缩方法》中介绍的BERT-of-Theseus挺相似的,只不过一个目的是蒸馏小模型,还是需要用到大模型来反向传播;而LST目的则是提升训练效率,不需要大模型来反向传播,但推理时需要用到大模型来前向传播。可以说两者有点互补了。
文章小结 #
本文主要介绍了同时具备参数高效和训练高效特点的一种大模型微调方法——Ladder Side-Tuning。
转载到请包括本文地址:https://spaces.ac.cn/archives/9138
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jun. 20, 2022). 《Ladder Side-Tuning:预训练模型的“过墙梯” 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/9138
@online{kexuefm-9138,
title={Ladder Side-Tuning:预训练模型的“过墙梯”},
author={苏剑林},
year={2022},
month={Jun},
url={\url{https://spaces.ac.cn/archives/9138}},
}










April 30th, 2023
[...]苏剑林. (Jun. 20, 2022). 《Ladder Side-Tuning:预训练模型的“过墙梯” 》[Blog post]. Retrieved from https://kexue.fm/archives/9138[...]
April 30th, 2023
[...]苏剑林. (Jun. 20, 2022). 《Ladder Side-Tuning:预训练模型的“过墙梯” 》[Blog post]. Retrieved from https://kexue.fm/archives/9138[...]
May 1st, 2023
[...]苏剑林. (Jun. 20, 2022). 《Ladder Side-Tuning:预训练模型的“过墙梯” 》[Blog post]. Retrieved from https://kexue.fm/archives/9138[...]
May 25th, 2023
好像被吞评论了
"""
def apply_main_layers(self, inputs, index):
x = super(LST_BERT, self).apply_main_layers(inputs, index)
n = (index + 1) * self.skip - 1
n = 'Expert-Transformer-%d-FeedForward-Norm' % n
y = self.expert_model.get_layer(n).output
y = keras.layers.Dense(self.hidden_size, use_bias=False)(y)
return keras.layers.Add()([x, y])
"""
苏老师,请问一下您这里的实现好像和原文不一样,您是最后相加的,而原文是先相加再进入adapter里的,是我理解有误吗,请赐教!
如果先相加,维度不同的话怎么加?
June 28th, 2023
苏神,请问下代码到底是如何实现反向传播不经过大模型的呀。 看了好久没弄明白。
直接按原理实现前向模型,优化器求梯度时就不会经过大模型。
July 6th, 2023
感谢苏神!!!我懂啦,模型就是正常流程实现,只是把要反向传播的参数传给优化器求梯度就行了
September 14th, 2023
为什么prompt tuning的显存占用要高于fully finetuning?
貌似没有?
October 4th, 2023
同问,根据他实验table1好像 prompt tuning 在戌年的时候显存占用很高,苏神您能分析下这是为什么吗
full fine-tuning不是17.6GB吗?prompt tuning不是11.6GB吗?哪里更高?
December 9th, 2023
他那个代码也太乱了,都不知道哪个项目是哪个项目,一堆sh文件