BERT-of-Theseus：基于模块替换的模型压缩方法

最近了解到一种称为“BERT-of-Theseus”的BERT模型压缩方法，来自论文《BERT-of-Theseus: Compressing BERT by Progressive Module Replacing》。这是一种以“可替换性”为出发点所构建的模型压缩方案，相比常规的剪枝、蒸馏等手段，它整个流程显得更为优雅、简洁。本文将对该方法做一个简要的介绍，给出一个基于bert4keras的实现，并验证它的有效性。

BERT-of-Theseus，原作配图

模型压缩 #

首先，我们简要介绍一下模型压缩。不过由于笔者并非专门做模型压缩的，也没有经过特别系统的调研，所以该介绍可能显得不专业，请读者理解。

基本概念 #

简单来说，模型压缩就是“简化大模型，得到推理速度更快的小模型”。当然，一般来说模型压缩是有一定牺牲的，比如最明显的是最后的评测指标会有一定的下降，毕竟“更好又更快”的免费午餐是很少的，所以选择模型压缩的前提是能允许一定的精度损失。其次，模型压缩的提速通常只体现在预测阶段，换句话说，它通常需要花费更长的训练时间，所以如果你的瓶颈是训练时间，那么模型压缩也不适合你。

模型压缩要花费更长时间的原因是它需要“先训练大模型，再压缩为小模型”。读者可能会疑惑：为什么不直接训练一个小模型？答案是目前很多实验已经表明，先训练大模型再压缩，相比直接训练一个小模型，最后的精度通常会更高一些。也就是说，在推理速度一样的情况，压缩得到的模型更优一些，相关探讨可以参考论文《Train Large, Then Compress: Rethinking Model Size for Efficient Training and Inference of Transformers》，另外知乎上也有讨论《为什么要压缩模型，而不是直接训练一个小的CNN？》。

常见手段 #

常见的模型压缩技术可以分为两大类：1、直接简化大模型得到小模型；2、借助大模型重新训练小模型。这两种手段的共同点是都先要训练出一个效果比较好的大模型，然后再做后续操作。

第一类的代表方法是剪枝（Pruning）和量化（Quantization）。剪枝，顾名思义，就是试图删减掉原来大模型的一些组件，使其变为一个小模型，同时使得模型效果在可接受的范围内；至于量化，指的是不改变原模型结构，但将模型换一种数值格式，同时也不严重降低效果，通常我们建立和训练模型用的是float32类型，而换成float16就能提速且省显存，如果能进一步转换成8位整数甚至2位整数（二值化），那么提速省显存的效果将会更加明显。

第二类的代表方法是蒸馏（Distillation）。蒸馏的基本想法是将大模型的输出当作小模型训练时的标签来用，以分类问题为例，实际的标签是one hot形式的，大模型的输出（比如logits）则包含更丰富的信号，所以小模型能从中学习到更好的特征。除了学习大模型的输出之外，很多时候为了更进一步提升效果，还需要小模型学习大模型的中间层结果、Attention矩阵、相关矩阵等，所以一个好的蒸馏过程通常涉及到多项loss，如何合理地设计这些loss以及调整这些loss的权重，是蒸馏领域的研究主题之一。

Theseus #

本文将要介绍的压缩方法称为“BERT-of-Theseus”，属于上面说的两大类压缩方法的第二类，也就是说它也是借助大模型来训练小模型，只不过它是基于模块的可替换性来设计的。

BERT-of-Theseus的命名源于思想实验“忒修斯之船”：如果忒修斯的船上的木头被逐渐替换，直到所有的木头都不是原来的木头，那这艘船还是原来的那艘船吗？

核心思想 #

前面说到，用蒸馏做模型压缩时，往往不仅希望小模型的输出跟大模型的输出对齐，还希望中间层结果也对齐。“对齐”意味着什么呢？意味着可替换！所以BERT-of-Theseus的思想就是：干嘛要煞费苦心地通过添加各种loss去实现可替换性呢？直接用小模型的模块去替换掉大模型的模块然后去训练不就好了吗？

举个实际的类比：

假设现在有A、B两支球队，每支各五人。A球队属于明星球队，实力超群；B球队则是新手球队，待训练。为了训练B球队，我们从B球队中选1人，替换掉A球队中的1人，然后让这个“4+1”的A球队不断的练习、比赛。经过一段时间，新加入的成员实体会提升，这个“4+1”的球队就拥有接近原始A球队的实力。重复这个过程，直到B球队的人都被充分训练，那么最终B球队的人也能自己组成一支实力突出的球队。 相比之下， 如果一开始就只有B球队，只是B球队的人自己训练、比赛，那么就算他们的实力逐渐提升，但由于没有实力超群的A球队帮助，其最终实力也不一定能突出。

流程细节 #

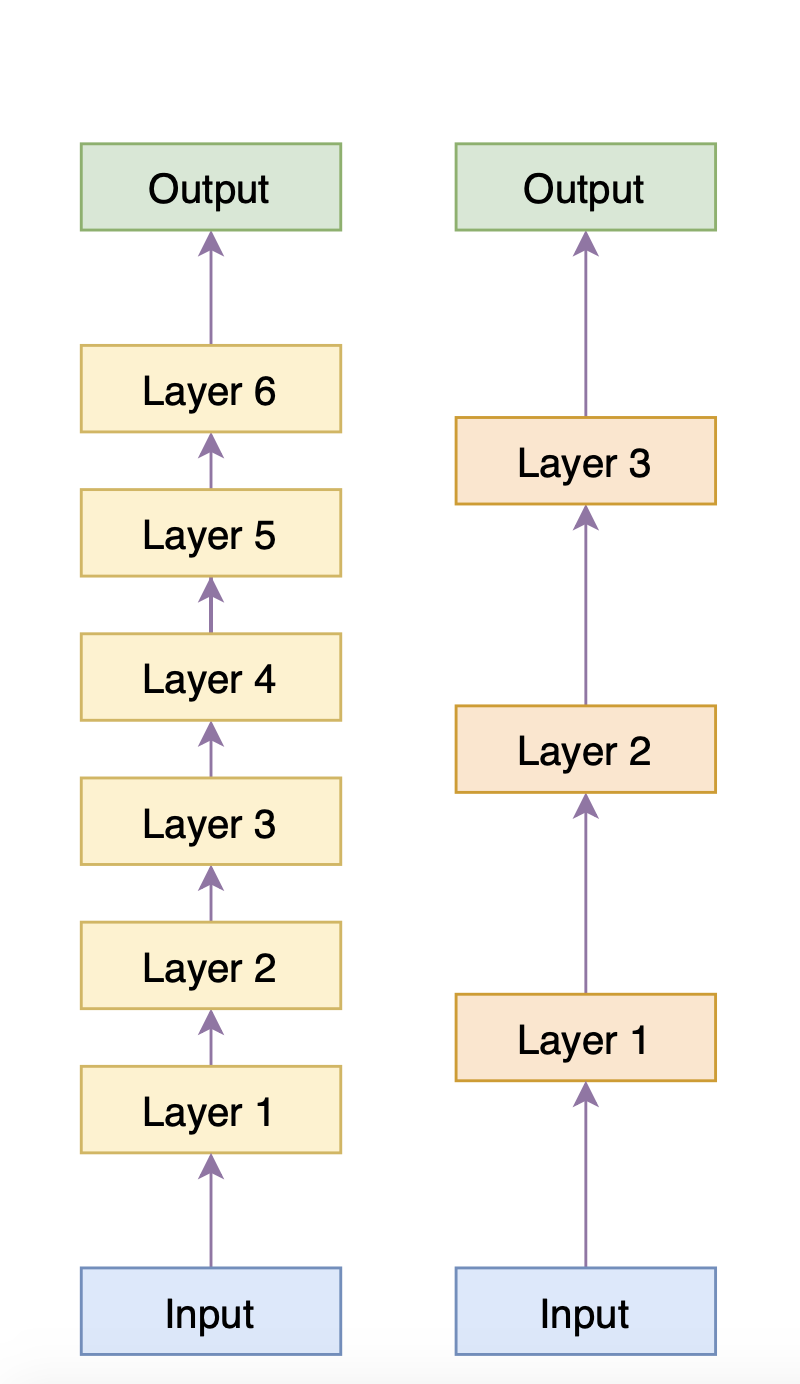
回到BERT的压缩，现在假设我们有一个6层的BERT，我们直接用它在下游任务上微调，得到一个效果还不错的模型，我们称之为Predecessor（前辈）；我们的目的是得到一个3层的BERT，它在下游任务中效果接近Predecessor，至少比直接拿BERT的前3层去微调要好（否则就白费力气了），这个小模型我们称为Successor（传承者）。那么BERT-of-Theseus是怎么实现这一点的呢？如下图（右）

Predecessor和Successor模型示意图

BERT-of-Theseus训练过程示意图

在BERT-of-Theseus的整个流程中，Predecessor的权重都被固定住。6层的Predecessor被分为3个模块，跟Successor的3层模型一一对应，训练的时候，随机用Successor层替换掉Predecessor的对应模块，然后直接用下游任务的优化目标进行微调（只训练Successor的层）。训练充分后，再把整个Successor单独分离出来，继续在下游任务中微调一会，直到验证集指标不再上升。

上述模型的等效模型

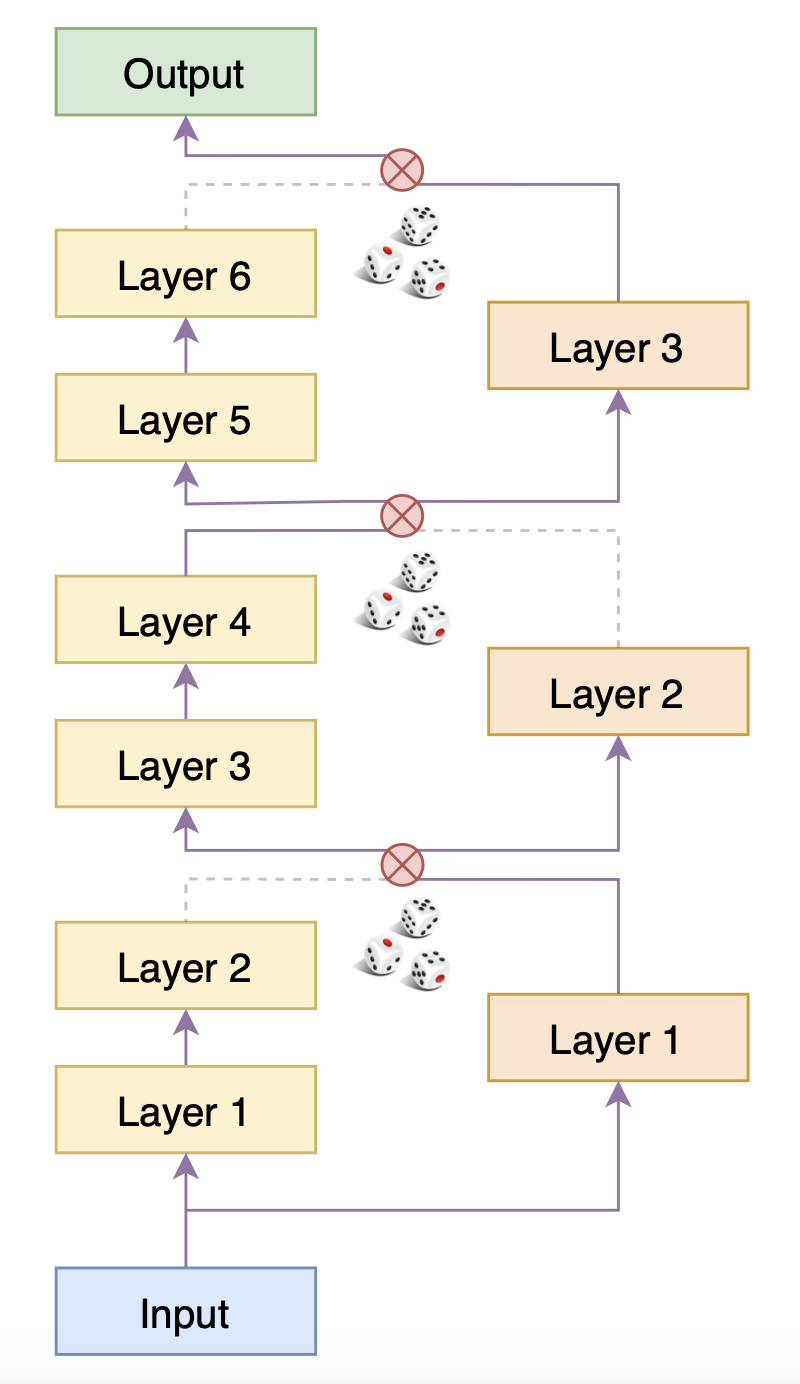
在实现的时候，事实上是类似Dropout的过程，同时执行Predecessor和Successor模型，并将两者对应模块的输出之一置零，然后求和、送入下一层中，即
\begin{equation}\begin{aligned}
&\varepsilon^{(l)}\sim U(\{0, 1\})\\
&x^{(l)} = x_p^{(l)} \times \varepsilon^{(l)} + x_s^{(l)} \times \left(1 - \varepsilon^{(l)}\right)\\
&x_p^{(l+1)} = F_p^{(l+1)}\left(x^{(l)}\right)\\
&x_s^{(l+1)} = F_s^{(l+1)}\left(x^{(l)}\right)
\end{aligned}\end{equation}
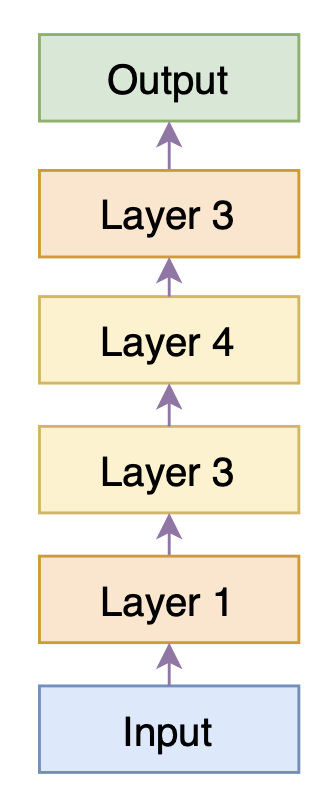
由于$\varepsilon$非0即1（不作调整，各自0.5概率随机选效果就挺好了），所以每个分支其实就相当于只有一个模块被选择到，因此上面右图就相当于右图的模型结构。由于每次的置零都是随机的，因此训练足够多的步数后，Successor的每个层都能被训练好。

方法分析 #

跟蒸馏相比，BERT-of-Theseus有什么优势呢？首先，这既然能被发表出来，所以至少效果应该是不相上下的，所以我们就不去比较效果了，而是比较方法本身。很明显，BERT-of-Theseus的主要特点是：简洁。

前面说到，蒸馏多数时候也需要匹配中间层输出，这时候要涉及到的训练目标就有很多了：下游任务loss、中间层输出loss、相关矩阵loss、Attention矩阵loss、等等，想想要平衡这些loss就是一件头疼的事情。相比之下，BERT-of-Theseus直接通过替换这个操作，逼着Successor能有跟Predecessor类似的输出，而最终的训练目标就只有下游任务loss，不可谓不简洁。此外，BERT-of-Theseus还有一个特别的优势：很多的蒸馏方法都得同时作用于预训练和微调阶段，效果才比较突出，而BERT-of-Theseus直接作用于下游任务的微调，就可以得到相媲美的效果。这个优势在算法上体现不出来，属于实验结论。

从形式上来看，BERT-of-Theseus的随机替换思路有点像图像中的数据扩增方案SamplePairing和mixup（参考《从SamplePairing到mixup：神奇的正则项》），都是随机采样两个对象加权求和来增强原模型；也有点像PGGAN的渐进式训练方案，都是通过对两个模型进行某种程度的混合，实现两个模型的过渡。如果了解它们的读者，继而就能够对BERT-of-Theseus提出一些拓展或者说疑问：$\varepsilon$一定要非0即1吗，任意$0\sim 1$的随机数行不？或者说不随机，直接让$\varepsilon$慢慢地从1变到0行不？这些想法都还没有经过充分实验，有兴趣的读者可以修改下述代码自行实验。

实验效果 #

原作者们开源了自己的PyTroch实现 JetRunner/BERT-of-Theseus，邱震宇老兄也分享了自己的讲解以及基于原版BERT的Tensorflow实现 qiufengyuyi/bert-of-theseus-tf。当然，既然笔者决定写这篇介绍，那就肯定少不了基于bert4keras的Keras实现了：

https://github.com/bojone/bert-of-theseus

这大概是目前最简洁、最具可读性的BERT-of-Theseus实现了，没有之一。

原论文的效果大家就自己去看原论文了。笔者在几个文本分类任务上实验了一下，结果大同小异，跟邱兄的实验结论也比较一致。其中在CLUE的iflytek数据集中实验结果如下：
$$\begin{array}{c|c|c}
\hline
& \text{直接微调} & \text{BERT-of-Theseus}\\
\hline
\begin{array}{c}\text{层数} \\ \text{效果}\end{array} & \begin{array}{ccc}\text{完整12层} & \text{前6层} & \text{前3层} \\ 60.11\% & 58.99\% & 57.96\%\end{array} & \begin{array}{cc}\text{6层} & \text{3层} \\ 59.61\% & 59.36\% \end{array}\\
\hline
\end{array}$$
可以看到，相比直接拿前几层微调，BERT-of-Theseus确实能带来一定的性能提升。对于随机置零方案，除了均等概率选择0/1外，原论文还尝试了其他策略，有轻微提升，但会引入额外超参，所以笔者就没有实验了，有兴趣的读者可以自己修改尝试。

另外，对于蒸馏来说，如果Successor跟Predecessor有同样的结构（同模型蒸馏），那么通常来说Successor的最终性能比Predecessor还要好些，BERT-of-Theseus有没有这一特点呢？笔者也实验了一下该想法，发现结论是否定的，也就是同模型情况下BERT-of-Theseus训练出来的Successor并没有比Predecessor好，所以看来BERT-of-Theseus虽好，但也不能完全取代蒸馏。

文末小结 #

本文介绍并实验了一种称为“BERT-of-Theseus”的BERT模型压缩方法，该方法的特点是简洁明了，纯粹通过替换操作来让小模型去学习大模型的行为，使得能在只有一个loss的情况下就能达到当前最优的模型压缩效果。

转载到请包括本文地址：https://spaces.ac.cn/archives/7575

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。