WGAN-div：一个默默无闻的WGAN填坑者

今天我们来谈一下Wasserstein散度，简称“W散度”。注意，这跟Wasserstein距离（Wasserstein distance，简称“W距离”，又叫Wasserstein度量、Wasserstein metric）是不同的两个东西。

本文源于论文《Wasserstein Divergence for GANs》，论文中提出了称为WGAN-div的GAN训练方案。这是一篇我很是欣赏却默默无闻的paper，我只是找文献时偶然碰到了它。不管英文还是中文界，它似乎都没有流行起来，但是我感觉它是一个相当漂亮的结果。

如果读者需要入门一下WGAN的相关知识，不妨请阅读拙作《互怼的艺术：从零直达WGAN-GP》。

WGAN #

我们知道原始的GAN（SGAN）会有可能存在梯度消失的问题，因此WGAN横空出世了。

W距离 #

WGAN引入了最优传输里边的W距离来度量两个分布的距离：
\begin{equation}W_c[\tilde{p}(x), q(x)] = \inf_{\gamma\in \Pi(\tilde{p}(x), q(x))} \mathbb{E}_{(x,y)\sim \gamma}[c(x,y)] \end{equation}
这里的$\tilde{p}(x)$是真实样本的分布，$q(x)$是伪造分布，$c(x,y)$是传输成本，论文中用的是$c(x,y)=\Vert x-y\Vert$；而$\gamma\in \Pi(\tilde{p}(x), q(x))$的意思是说：$\gamma$是任意关于$x, y$的二元分布，其边缘分布则为$\tilde{p}(x)$和$q(y)$。直观来看，$\gamma$描述了一个运输方案，而$c(x,y)$则是运输成本，$W_c[\tilde{p}(x), q(x)]$就是说要找到成本最低的那个运输方案所对应的成本作为分布度量。

对偶问题 #

W距离确实是一个很好的度量，但显然不好算。当$c(x,y)=\Vert x-y\Vert$时，我们可以将其转化为对偶问题：
\begin{equation}W(\tilde{p}(x), q(x)) = \sup_{\Vert T\Vert_L\leq 1} \mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] - \mathbb{E}_{x\sim q(x)}[T(x)]\label{eq:wgan-d}\end{equation}
其中$T(x)$是一个标量函数，$\Vert T\Vert_L$则是Lipschitz范数：
\begin{equation}\Vert T\Vert_L = \max_{x\neq y} \frac{|T(x)-T(y)|}{\Vert x - y\Vert}\end{equation}
说白了，$T(x)$要满足：
\begin{equation}|T(x)-T(y)| \leq \Vert x - y\Vert\end{equation}

生成模型 #

这样一来，生成模型的训练，可以作为W距离下的一个最小-最大问题：
\begin{equation}\mathop{\text{argmin}}_{G}\mathop{\text{argmax}}_{T,\Vert T\Vert_L\leq 1} \mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] - \mathbb{E}_{x\sim q(z)}[T(G(z))]\end{equation}
第一个$\text{argmax}$试图获得W距离的近似表达式，而第二个$\text{argmin}$则试图最小化W距离。

然而，$T$不是任意的，需要满足$\Vert T\Vert_L\leq 1$，这称为Lipschitz约束（L约束），该怎么施加这个约束呢？因此，一方面，WGAN开创了GAN的一个新流派，使得GAN的理论上了一个新高度，另一方面，WGAN也挖了一个关于L约束的大坑，这个坑也引得不少研究者前仆后继地...（跳坑？）

L约束 #

目前，往模型中加入L约束，有三种主要的方案。

权重裁剪 #

这是WGAN最原始的论文所提出的一种方案：在每一步的判别器的梯度下降后，将判别器的参数的绝对值裁剪到不超过某个固定常数。

这是一种非常朴素的做法，现在基本上已经不用了。其思想就是：L约束本质上就是要网络的波动程度不能超过一个线性函数，而激活函数通常都满足这个条件，所以只需要考虑网络权重，最简单的一种方案就是直接限制权重范围，这样就不会抖动太剧烈了。

梯度惩罚 #

这种思路非常直接，即$\Vert T\Vert_L\leq 1$可以由$\Vert \nabla T\Vert \leq 1$来保证，所以干脆把判别器的梯度作为一个惩罚项加入到判别器的loss中：
\begin{equation}T=\mathop{\text{argmin}}_{T} -\mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] + \mathbb{E}_{x\sim q(x)}[T(x)] + \lambda \mathbb{E}_{x\sim r(x)}\Big[\big(\Vert \nabla T\Vert - 1\big)^2\Big]\end{equation}
但问题是我们要求$\Vert T\Vert_L\leq 1$是在每一处都成立，所以$r(x)$应该是全空间的均匀分布才行，显然这很难做到。所以作者采用了一个非常机智（也有点流氓）的做法：在真假样本之间随机插值来惩罚，这样保证真假样本之间的过渡区域满足L约束。

这种方案就是WGAN-GP。显然，它比权重裁剪要高明一些，而且通常都work得很好。但是这种方案是一种经验方案，没有更完备的理论支撑。

谱归一化 #

另一种实现L约束的方案就是谱归一化（SN），可以参考我之前写考《深度学习中的Lipschitz约束：泛化与生成模型》。

本质上来说，谱归一化和权重裁剪都是同一类方案，只是谱归一化的理论更完备，结果更加松弛。而且还有一点不同的是：权重裁剪是一种“事后”的处理方案，也就是每次梯度下降后才直接裁剪参数，这种处理方案本身就可能导致优化上的不稳定；谱归一化是一种“事前”的处理方案，它直接将每一层的权重都谱归一化后才进行运算，谱归一化作为了模型的一部分，更加合理一些。

尽管谱归一化更加高明，但是它跟权重裁剪一样存在一个问题：把判别器限制在了一小簇函数之间。也就是说，加了谱归一化的$T$，只是所有满足L约束的函数的一小部分。因为谱归一化事实上要求网络的每一层都满足L约束，但这个条件太死了，也许这一层可以不满足L约束，下一层则满足更强的L约束，两者抵消，整体就满足L约束，但谱归一化不能适应这种情况。

WGAN-div #

在这种情况下，《Wasserstein Divergence for GANs》引入了W散度，它声称：现在我们可以去掉L约束了，并且还保留了W距离的好性质。

论文回顾 #

有这样的好事？我们来看看W散度是什么。一上来，作者先回顾了一些经典的GAN的训练方案，然后随手扔出一篇文献，叫做《Partial differential equations and monge-kantorovich mass transfer》，里边提供了一个方案（下面的出场顺序跟论文有所不同），能直接将$T$训练出来，目标是（跟原文的写法有些不一样）
\begin{equation}T^* = \mathop{\text{argmax}}_{T} \mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] - \mathbb{E}_{x\sim q(x)}[T(x)] - \frac{1}{2}\mathbb{E}_{x\sim r(x)}[\Vert \nabla T\Vert^2]\label{eq:wgan-div-d1}\end{equation}
这里的$r(x)$是一个非常宽松的分布，我们后面再细谈。整个loss的意思是：你只要按照这个公式将$T$训练出来，它就是$\eqref{eq:wgan-d}$式中的$T$的最优解，也就是说，接下来只要把它代进$\eqref{eq:wgan-d}$式，就得到了W距离，最小化它就可以得到生成器了。
\begin{equation}\mathop{\text{argmin}}_{G}\mathbb{E}_{x\sim \tilde{p}(x)}[T^*(x)] - \mathbb{E}_{x\sim q(z)}[T^*(G(z))]\label{eq:wgan-div-g1}\end{equation}

一些注解 #

首先，我为什么说作者“随手”跑出一篇论文呢？因为作者确实是随手啊...

作者直接说“According to [19]”，然后就给出了后面的结果，[19]就是这篇论文，是一篇最优传输和偏微分方程的论文，59页...我翻来翻去，才发现作者引用的应该是36页和40页的结果（不过翻到了也没能进一步看懂，放弃了），也不提供多一点参考资料，尴尬～～还有后面的一些引理，作者也说“直接去看[19]的discussion吧”.....

然后，读者更多的疑问是：这玩意跟梯度惩罚方案有什么差别，加个负号变成最小化不都是差不多吗？做实验时也许没有多大差别，但是理论上的差别是很大的，因为WGAN-GP的梯度惩罚只能算是一种经验方案，而$\eqref{eq:wgan-div-d1}$式是有理论保证的。后面我们会继续讲完它。

W散度 #

式$\eqref{eq:wgan-div-d1}$是一个理论结果，而不管怎样深度学习还是一门理论和工程结合的学科，所以作者一般化地考虑了下面的目标
\begin{equation}W_{k,p}[\tilde{p}(x), q(x)] = \max_{T} \mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] - \mathbb{E}_{x\sim q(x)}[T(x)] - k\mathbb{E}_{x\sim r(x)}[\Vert \nabla T\Vert^p]\label{eq:wdiv}\end{equation}
其中$k > 0, p > 1$。基于此，作者证明了$W_{k,p}$有非常好的性质：

1、$W_{k,p}$是个对称的散度。散度的意思是：$\mathcal{D}[P,Q]\geq 0$且$\mathcal{D}[P,Q]=0\Leftrightarrow P=Q$，它跟“距离”的差别是它不一定满足三角不等式，也有叫做“半度量”、“半距离”的。$W_{k,p}$是一个散度，这已经非常棒了，因为我们大多数GAN都只是在优化某个散度而已。散度意味着当我们最小化它时，我们真正是在缩小两个分布的距离。

2、$W_{k,p}$的最优解跟W距离有一定的联系。$\eqref{eq:wgan-div-d1}$式就是一个特殊的$W_{1/2,2}$。这说明当我们最大化$W_{k,p}$得到$T$之后，可以去掉梯度项，通过最小化$\eqref{eq:wgan-div-g1}$来训练生成器。这也表明以$W_{k,p}$为目标，性质跟W距离类似，不会有梯度消失的问题。

3、这是我觉得最逗的一点，作者证明了
\begin{equation}\max_{T} \mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] - \mathbb{E}_{x\sim q(x)}[T(x)] - k\mathbb{E}_{x\sim r(x)}[(\Vert \nabla T\Vert - n)^p]\end{equation}
不总是一个散度。当$n=1,p=2$时这就是WGAN-GP的梯度惩罚，作者说它不是一个散度，明摆着要跟WGAN-GP对着干，哈哈哈～～不是散度意味着WGAN-GP在训练判别器的时候，并非总是会在拉大两个分布的距离（鉴别者在偷懒，没有好好提升自己的鉴别技能），从而使得训练生成器时回传的梯度不准。

WGAN-div #

好了，说了这么久，终于可以引入WGAN-div了，其实就是基于$\eqref{eq:wdiv}$的WGAN的训练模式了：
\begin{equation}\begin{aligned}T =& \mathop{\text{argmax}}_{T} \mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] - \mathbb{E}_{x\sim q(x)}[T(x)] - k\mathbb{E}_{x\sim r(x)}[\Vert \nabla T\Vert^p]\\
G =& \mathop{\text{argmin}}_{G} \mathbb{E}_{x\sim \tilde{p}(x)}[T(x)] - \mathbb{E}_{x\sim q(z)}[T(G(z))]\end{aligned}\end{equation}
前者是为了通过W散度$W_{k,p}$找出W距离中最优的$T$，后者就是为了最小化W距离。所以，W散度的角色，就是一个为W距离的默默无闻的填坑者呀，再结合这篇论文本身的鲜有反响，我觉得这种感觉更加强烈了。

实验 #

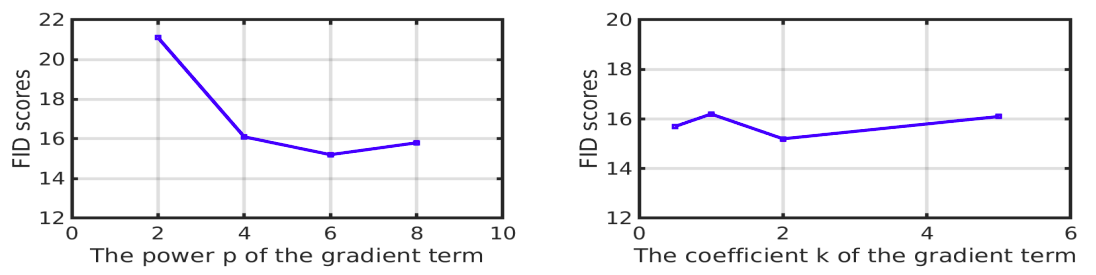
k,p的选择 #

作者通过做了一批搜索实验，发现$k=2,p=6$时效果最好（用FID为指标）。这进一步与WGAN-GP的做法有出入：范数的二次幂并非是最好的选择。

不同的k,p对FID的影响（FID越小越好）

r(x)的选择 #

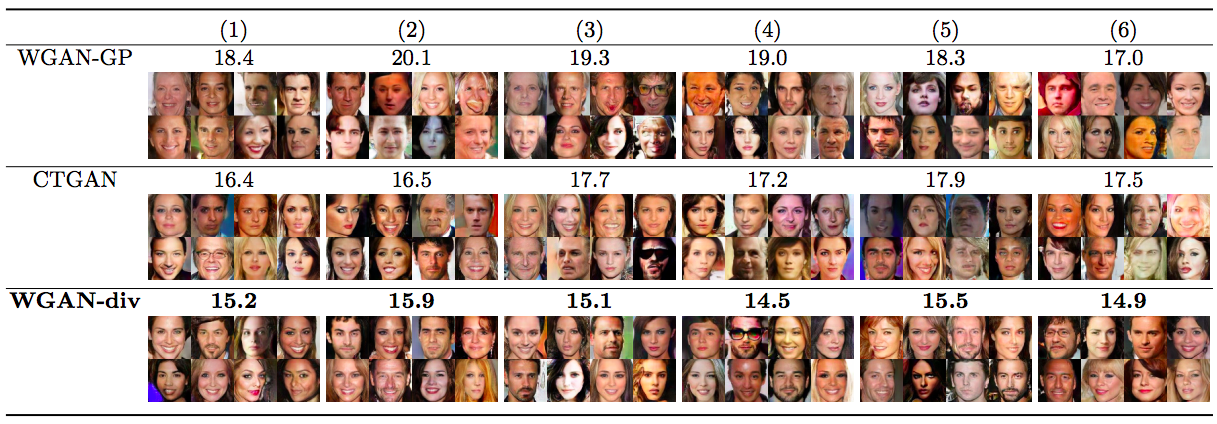
前面我们就说过，W散度中对$r(x)$的要求非常宽松，论文也做了一组对比实验，对比了常见的做法：

1、真假样本随机插值；

2、真样本之间随机插值、假样本之间随机插值；

3、真假样本混合后，随机选两个样本插值；

4、直接选原始的真假样本混合；

5、直接只选原始的假样本；

6、直接只选原始的真样本。

结果发现，在WGAN-div之下这几种做法表现都差不多（用FID为指标），但是对于WGAN-GP，这几种做法差别比较大，而且WGAN-GP中最好的结果比WGAN-div中最差的结果还要差。这时候WGAN-GP就被彻底虐倒了...

不同的采样方式所导致的不同模型的FID不同差异（FID越小越好）

这里边的差别不难解释，WGAN-GP是凭经验加上梯度惩罚，并且“真假样本随机插值”只是它无法做到全空间采样的一个折衷做法，但是W散度和WGAN-div，从理论的开始，就没对$r(x)$有什么严格的限制。其实，原始W散度的构造（这个需要看参考论文）基本上只要求$r(x)$是一个样本空间跟$\tilde{p}(x)、q(x)$一样的分布，非常弱的要求，而我们一般选择为$\tilde{p}(x)、q(x)$两者共同衍生出来的分布，相对来说收敛快一点。

参考代码 #

自然是用Keras写的～人生苦短，我用Keras
https://github.com/bojone/gan/blob/master/keras/wgan_div_celeba.py

随机样本（自己的实验结果）：

WGAN-div的部分样本（2w iter）

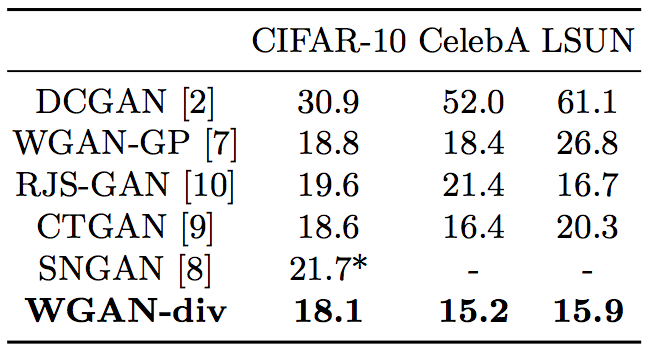
当然，原论文的实验结果也表明WGAN-div是很优秀的：

WGAN-div与不同的模型在不同的数据集效果比较（指标为FID，越小越好）

结语 #

不知道业界是怎么看这篇WGAN-div的，也许是觉得跟WGAN-GP没什么不同，就觉得没有什么意思了。不过我是很佩服这些从理论上推导并且改进原始结果的大牛及其成果。虽然看起来像是随手甩了一篇论文然后说“你看着办吧”的感觉，但这种将理论和实践结合起来的结果仍然是很有美感的。

本来我对WGAN-GP是多少有些芥蒂的，总觉得它太丑，不想用。但是WGAN-div出现了，在我心中已经替代了WGAN-GP，并且它不再丑了～

转载到请包括本文地址：https://spaces.ac.cn/archives/6139

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。