高考成绩出来了，不是很理想，不能进入很理想的高校。不过不管到了哪里，我都会一直延续我的科学梦，醉心于数学物理研究。昨天志愿填报也完成了，所以高考的事情暂时也告一段落了，接着就等通知了。

接下来的几篇文章可能会探讨一些有趣的轨迹问题，是和圆锥曲线有关的，它们基本都是在高考前两周的时间内完成的。先看最简单的一个，抛物线$y=x^2$内有一条定长为a的弦，求弦的中点轨迹，并探讨轨迹的最低点位置。

抛物线里边的定长弦

抛物线里边的定长弦

可以设想一个对应的物理模型，一个旋转抛物线形状的大碗，一个筷子在里边滑下来，求中点的轨迹。那么中点的最低点意味着什么呢？根据重力势能的定义，中点最低意味着势能最小，而之前的“势能最小原理”告诉我们势能最小意味着平衡，原来中点最低其实对应着这根筷子的稳定位置。

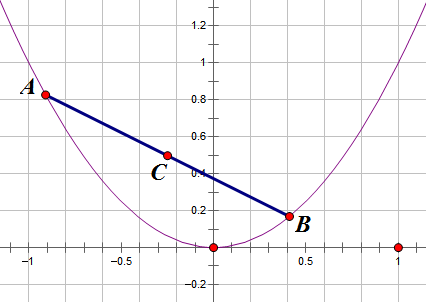
先来求轨迹。如图，设$A=(x_1,y_1),B=(x_2,y_2)$，结合$y=x^2$，可以列出关系式

$$(x_1-x_2)^2+(x_1^2-x_2^2)^2=a^2$$

中点的表达式为

$$x=\frac{x_1+x_2}{2},y=\frac{x_1^2+x_2^2}{2}$$

这个表达形式要求我们要尽量把距离关系式往$x_1+x_2$和$x_1^2+x_2^2$靠拢，其过程为

$$\begin{aligned}(x_1-x_2)^2[1+(x_1+x_2)^2]=a^2 \\ [2(x_1^2+x_2^2)-(x_1+x_2)^2][1+(x_1+x_2)^2]=a^2\end{aligned}$$

所以轨迹方程就是

$$4(y-x^2)(1+4x^2)=a^2$$

或者写成$4y=\frac{a^2}{1+4x^2}+4x^2$

现在来探讨轨迹的最低点位置。即求y的最小值，由基本不等式可以得到：

$$4y=\frac{a^2}{1+4x^2}+(1+4x^2)-1 \geq 2\sqrt{\frac{a^2}{1+4x^2}\cdot (1+4x^2)}-1=2a-1$$

即$y_min=\frac{2a-1}{4}$，但是有个限制条件，取等号的条件为：$\frac{a^2}{1+4x^2}=1+4x^2$，这要求$a \geq 1$。

当$a \leq 1$时，容易发现x=0的时候取到最小值$y_{min}=\frac{a^2}{4}$。

不同的a值对应的图像如下：

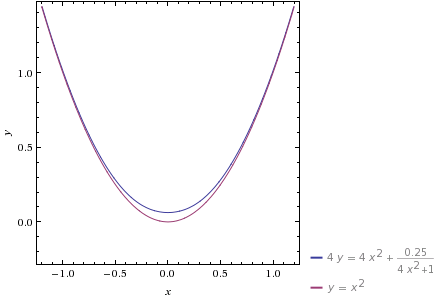
a=0.5时的图像

a=0.5时的图像

a=0.5时的图像

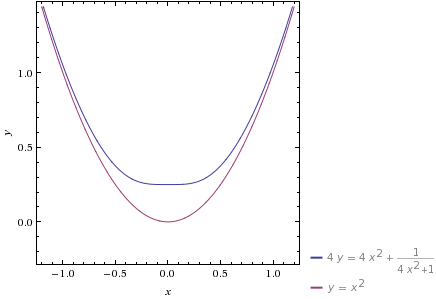
a=1时的图像

a=1时的图像

a=1时的图像

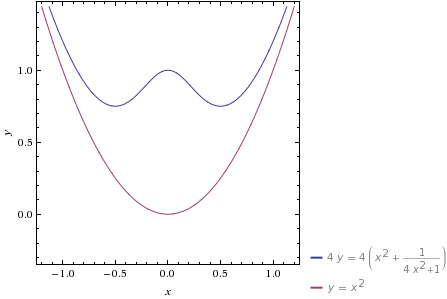
a=2时的图像

a=2时的图像

a=2时的图像

之前已经说过，最低点就是那根“筷子”的平衡位置。可是受力分析告诉我们，当AB平行于x轴时（水平位置），筷子也是受力平衡的，应该也属于平衡点呀，为什么所求的不是这个点呢？其实一个系统往往有多个平衡位置，但并非每一个平衡位置都是稳定的。稳定的平衡位置在受到轻微干扰后，只会围绕着平衡点轻微地摆动，而不稳定的平衡点在受到轻微干扰，会远远偏离原来状态。比如，我们轻轻地晃动这个碗，那么这个筷子会怎么摆动呢？在原来的位置稍微摆动，意味着它是稳定的；远离原来的位置，到了另外一个位置，意味着它是不稳定的——尽管它们都是受力平衡点。

对于抛物线是$y=kx^2$的形式的轨迹，可以通过换元变成本文的形式，所以不再赘述。一个很容易想到的问题是：将本文的曲线改成是一个椭圆，那么定长弦的中点轨迹又是怎样的？这将在下一篇文章讲到。

转载到请包括本文地址：https://spaces.ac.cn/archives/1639

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jun. 30, 2012). 《抛物线内一根定长的弦 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1639

@online{kexuefm-1639,
        title={抛物线内一根定长的弦},
        author={苏剑林},
        year={2012},
        month={Jun},
        url={\url{https://spaces.ac.cn/archives/1639}},
}