无固定点的单摆运动

我们经常听说牛顿力学、相对论力学、量子力学等物理名词，也不时会听到“理论力学”。其实，“理论力学”这个名词是不大妥当的，因为这很容易会让人误认为这是一种新的力学体系。而事实上，理论力学并不是像牛顿力学那样是一种力学体系，而是一种研究力学的方法，而研究的对象在多数情况下依然是经典力学（翻开任意一本《理论力学》教程都不难发现这一点）。简单来讲，它把牛顿时代用微积分来研究力学的方法转变为了“变分”，变“常微分”为“偏微分”。看上去这有点“化简为繁”，但事实上这样的一个转变却带来了力学研究的一个巨大的飞跃。

说到这里，也许有的读者会感到害怕了：这里边肯定又涉及了各种高深莫测的高等数学方法，我们只能望而却步。的确，理论力学中的方法很是深奥，纵使是一个优秀的大学数理本科生，也可能要花上一年多时间才能学完一本《理论力学》。可是，通过最小作用量原理的方法去研究物理又显得如此地诱人。难道像我们这些初级人士就无法亲身体验理论力学方法给我们带来的巨大便利和不一样的体验了吗？

其实也不尽然，只有读者拥有基本的微积分知识（常微分、偏微分、积分等）和足够的耐心，我们还是有能力去了解一下理论力学（或者说最小作用量原理）是怎么发挥作用的。当然，读者还需要有一些理论力学基础，至少，你得知道最小作用量和最小作用量原理（在经典力学框架下的）是什么。下面我们就来探究“无固定点的单摆运动”。

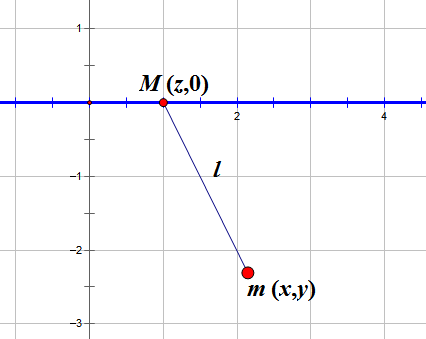
如图，一质量为M的圆环套在水平光滑轴上，环系一条长度为l的细绳，绳的另一端系一个质量为m的重物。分析该摆的运动。我们已经选取了适当的坐标系，使得t=0时为释放瞬间（即各速度为0）。

我们需要完成以下步骤：

1、用若干坐标为所研究的系统进行“定位”；
2、写出该系统各对象的动能T和势能U，继而写出拉格朗日函数L=T-U；
3、写出该系统各对象的坐标之间相互的约束条件；
4、利用约束条件对L进行化简（即去除掉不独立的坐标）；
5、将L代入拉格朗日方程，得到系统的运动方程。

首先我们用直角坐标(x,y)来定位m，用(z,0)来定位M。容易写出两者的总动能为$T=1/2 m(\dot{x}^2+\dot{y}^2)+1/2 M \dot{z}^2$，而势能是$U=mg(l-y)+Mgl$（选取在光滑轴下方l处的水平平面为零势面）。

我们注意到，x,y,z不是独立的，它们之间有约束条件：$(x-z)^2+y^2=l^2$，换句话说，它们之间只有两个独立坐标。为了研究的方便，我们采取换元法将其化简，即令$y=l \cos\theta$，则$x=z+l \sin\theta$。即我们用θ和z作为我们研究的独立坐标。于是动能变为$T=1/2 [(M+m)\dot{z}^2+ml^2 \dot{\theta}^2+2ml \cos\theta \dot{\theta} \dot{z}]$，而势能$U=mgl(1-\cos\theta)+Mgl$。

拉格朗日函数
$$L=1/2 [(M+m)\dot{z}^2+ml^2 \dot{\theta}^2+2ml \cos\theta \dot{\theta} \dot{z}]-mgl(1-\cos\theta)-Mgl\tag{1}$$
代入拉格朗日方程，有
$$\frac{d}{dt}\frac{\partial L}{\partial \dot{z}}=\frac{d}{dt}[(M+m)\dot{z}+mlcos\theta \dot{\theta}]=\frac{\partial L}{\partial z}=0\tag{1}$$立马得到
$$(M+m)\dot{z}+mlcos\theta \dot{\theta}=C_1\tag{2}$$可以再积分一次
$$(M+m)z+mlsin\theta=C_1 t+C_2\tag{3}$$
根据初始条件，应该有$C_1=0,C_2=mlsin\theta_0$。(3)变为
$$(M+m)z+mlsin\theta=mlsin\theta_0\tag{4}$$
由此，我们知道M点的运动被约束在$(\frac{ml(sin\theta_0-1)}{M+m},\frac{ml(sin\theta_0+1)}{M+m})$区域内。

另外，我们有能量守恒：T+U=常数，即
$$E=1/2 [(M+m)\dot{z}^2+ml^2 \dot{\theta}^2+2ml \cos\theta \dot{\theta} \dot{z}]+mgl(1-\cos\theta)+Mgl=C_3\tag{5}$$
(4)、(5)联合起来，就可以对整个运动过程进行描述。要知道，对此，我们并没有进行任何受力分析，就得到了运动方程及其一些初级积分；而且对于能量函数的操作，我们也感到很是“顺手”，并没有什么被“卡住”的感觉，这都能让我们感受到理论力学研究方法的便利。假如用牛顿第二定律，则必须仔细地辨明所有的相关作用力。这是一项既困难又容易出错的工作。接下来，由(3)可以得到
$$\dot{z}=-\frac{mlcos\theta \dot{\theta}}{M+m}$$

代入(5)得到
$$E=\frac{ml^2 \dot{\theta}^2}{2(M+m)}(M+m \sin^2 \theta)+mgl(1-\cos\theta)+Mgl=C_3\tag{6}$$
由(6)以及初始条件得到$C_3=mgl(1-cos\theta_0)+Mgl$。所以有
$$\dot{\theta}^2=\frac{2g(\cos\theta-\cos\theta_0)(M+m)}{Ml+ml \sin^2\theta}\tag{7}$$
要是能够解出(7)，就可能完整地对整个运动进行描述了。很可惜的是，(7)很难求解。我们现在只考虑几种极限情况：

一、θ很小时（小振幅）

我们以$1-\frac{\theta^2}{2}$代替$cos\theta$，以0代替$sin^2 \theta$（处于分母的项的“地位”更低，更容易被我们忽略），则(7)可以简化为

$$\dot{\theta}^2=\frac{g(M+m)}{Ml}(\theta_0^2-\theta^2)\tag{8}$$
解得$$\theta=\theta_0 \cos(\sqrt{\frac{g(M+m)}{Ml}} t)\tag{9}$$
由此可看出小振幅的周期为$T=2\pi \sqrt{\frac{Ml}{g(M+m)}}$。同时由(7)式表明此种情况下M不能过小，否则会导致分母发散，使得近似处理变得没有意义。

二、M趋于无穷大时

此时，(7)变为
$$\dot{\theta}^2=2g(\cos\theta-\cos\theta_0)\tag{10}$$
这和固定点的单摆运动方程一致，可以参考这里。不再赘述。

三、M=0时

这个特殊情况足以让我们一睹无固定点单摆运动的诡异。

在此种情况下，(7)变为
$$\dot{\theta}^2=\frac{2g(\cos\theta-\cos\theta_0)}{l \sin^2\theta}\tag{11}$$
即$t=-\sqrt{\frac{l}{2g}}\int sin\theta\sqrt{\frac{1}{cos\theta-cos\theta_0}} d\theta$
（想想这里为什么要取负号？）

这可以很简单地精确积分，即
$$t=\sqrt{\frac{l}{2g}}\int \sqrt{\frac{1}{\cos\theta-\cos\theta_0}} d(\cos\theta)=\sqrt{\frac{2l}{g}(\cos\theta-\cos\theta_0)}+C_4$$

容易得出$C_4=0$，那么得到
$$\cos\theta=\cos\theta_0+\frac{g t^2}{2l}\tag{12}$$
(12)意味着什么？意味着运动时间仅为$t=\sqrt{\frac{2l}{g}(1-cos\theta_0)}$。

这显然与我们的直觉相违。而且根据能量守恒，它也决不可能就此停止下来。那么，此时会发生什么呢？

接下来的情况就变得很混沌了....（待续）

转载到请包括本文地址：https://spaces.ac.cn/archives/1344

更详细的转载事宜请参考：《科学空间FAQ》