9 Jun

捉弄计划的失败——单摆周期

By 苏剑林 | 2010-06-09 | 48142位读者 |

老式机械摆钟

“滴答滴答，滴答滴答——”当我们看到家里的摆钟来回摆动，并且能够准确地报时的时候，有没有想过其中的奥妙呢？

有一天，你想捉弄一下妈妈，把钟摆系上一个重物，心想着钟一定会走得更快，妈妈就会乱套了。可是很快你会失望地发现，摆钟依然准时地走着，没有任何异常，时间仿佛在宣告他的不可控制。你感到非常纳闷：为什么我的计划会失败呢？

据说，世界上第一个研究单摆的人是伽利略，他通过多次实验得出结论：单摆的周期只取决于摆绳的长度，和摆的重量无关。这是你明白了，原来要捉弄妈妈，应该要增加钟摆长度才对...^_^

现在我们来分析一下这个单摆....

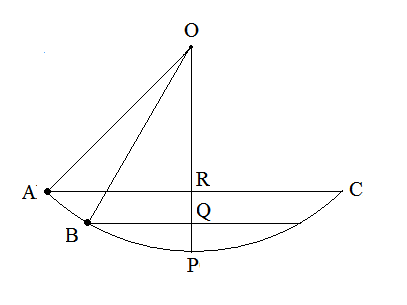
单摆示意图

设单摆的长度为l，在下落过程中只考虑重力因素，那么机械能是守恒的。点A是始点，此时速度为0；当摆下落到B点后，速度为v，动能为 $1/2 mv^2$ ，动能是由重力势能转化而来的，设 $RQ=h=l(\cos\theta-\cos\theta_0)$ ，重力势能的减少量为 $mgh=mgl(\cos\theta-\cos\theta_0)$ 。于是我们可以列出

$\begin{aligned}v^2=2gl(\cos\theta-\cos\theta_0)=(\frac{ds}{dt})^2=(l\frac{d\theta}{dt})^2 \\ \frac{d\theta}{dt}=\sqrt{\frac{2g}{l}}\sqrt{\cos\theta-\cos\theta_0}\end{aligned}$

利用 $cos\theta=1-2sin^2 \frac{\theta}{2}$ ，可以变换成

$\frac{dt}{d\theta}=1/2 \sqrt{\frac{l}{g}}\frac{1}{\sqrt{\sin^2 \frac{\theta_0}{2}-\sin^2 \frac{\theta}{2}}}$

对于摆来说，一个周期T定义为从A点到达C点再回到A点所用的时间，由于从A—P与从P—C所用时间是相同的，所以 $T=4T_{AP}$ ，即

$T=4\int_0^{\theta_0} 1/2 \sqrt{\frac{l}{g}}\frac{d\theta}{\sqrt{\sin^2 \frac{\theta_0}{2}-\sin^2 \frac{\theta}{2}}}$

单摆动画

实际上，对于不同的 $\theta_0$ ，这个积分的结果是不一样的，但是为什么高中书本上都说周期和角度无关呢？当 $\theta$ 比较小的时候，我们用关系式 $sin^2 \frac{\theta}{2}\approx (\frac{\theta}{2})^2$ ，替换后变成

$T=4\sqrt{\frac{l}{g}}\int_0^{\theta_0} \frac{d\theta}{\sqrt{\theta_0^2-\theta^2}}$

由定积分的知识可以知道，结果为 $T=2\pi \sqrt{\frac{l}{g}}$ ，这正是伽利略的结果，与质量、初始角度无关。

如果需要精确的算法，可以从以下方向思考：

令 $sin\frac{\theta_0}{2}=k,sin\frac{\theta}{2}=k sin\varphi$ ， $\varphi \in(0,\frac{\pi}{2})$ ,则 $1/2 cos\frac{\theta}{2}d\theta=kcos\varphi$ ，即

$d\theta=\frac{2k \cos\varphi d\varphi }{\sqrt{1-k^2 \sin^2 \varphi}}$

代入后得到

$T=4\sqrt{\frac{l}{g}}\int_0^{\frac{\pi}{2}} \frac{1}{\sqrt{1-k^2 \sin^2 \varphi}}$

这类积分成为“第一类椭圆积分”。其结果为：

$T=2\pi\sqrt{\frac{l}{g}}(1+\frac{1}{2^2}\sin^2 \frac{\theta}{2}+\frac{1\cdot 3^2}{2^2\cdot 4^2}\sin^4 \frac{\theta}{2}+...)$

如果只取到第一项，那么就是刚开始的近似公式。推导过程可以查阅大学的《数学分析》教程，或者参考下边的图片。

第一类椭圆积分

数学传播-单摆的详细分析.pdf

转载到请包括本文地址：https://spaces.ac.cn/archives/674

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jun. 09, 2010). 《捉弄计划的失败——单摆周期》[Blog post]. Retrieved from https://spaces.ac.cn/archives/674

@online{kexuefm-674,
        title={捉弄计划的失败——单摆周期},
        author={苏剑林},
        year={2010},
        month={Jun},
        url={\url{https://spaces.ac.cn/archives/674}},
}

分类：物理化学标签：周期, 积分, 椭圆, 简谐, 振动 3 评论

< 作文《人与路》 | 祝大家端午节快乐！ >

你也许还对下面的内容感兴趣

发表你的看法

zzm

June 14th, 2010

课本上说那个公式叫惠更斯公式
这种方法太复杂了吧

回复评论

苏剑林发表于 June 15th, 2010

这是从相对严格的数学和物理理论角度进行推导。
我比较反感书本上的粗略公式。
我比较喜欢对一些定理进行比较严密的推导——哪怕最后的结果也只能是近似的。

回复评论

银色立方体

July 20th, 2010

　　据说，若不考虑各种摩擦阻滞情况，只有在摆线曲面上滚动的球滚动周期才是严格等时的，不像单摆要考虑摆动幅度的大小。

回复评论

SEARCH

MENU

CATEGORIES

NEWPOSTS

COMMENTS

USERLOGIN

捉弄计划的失败——单摆周期

你也许还对下面的内容感兴趣

关于站长

智能搜索

热门标签

随机文章

最近评论

友情链接