本文我们来探讨下列积分的极值曲线:
$$S=\int f(x,y)\sqrt{dx^2+dy^2}=\int f(x,y)ds$$
这本质上也是一个短程线问题。但是它形式比较简答,物理含义也更加明显。比如,如果$f(x,y)$是势函数的话,那么这就是一个求势能最小的二维问题;如果$f(x,y)$是摩擦力函数,那么这就是寻找摩擦力最小的路径问题。不管是哪一种,该问题都有相当的实用价值。下面将其变分:
$$\begin{aligned} \delta S =&\int \delta[f(x,y)\sqrt{dx^2+dy^2}] \\ =&\int [ds\delta f(x,y)+f(x,y)\frac{\delta (dx^2+dy^2)}{2ds}]\\ =&\int ds(\frac{\partial f}{\partial x}\delta x+\frac{\partial}{\partial y}\delta y)+f \frac{dx d(\delta x)+dy d(\delta y)}{ds} \\=&\int ds(\frac{\partial f}{\partial x}\delta x+\frac{\partial}{\partial y}\delta y)+f \frac{dx}{ds} d(\delta x)+\frac{dy}{ds} d(\delta y) \end{aligned}$$
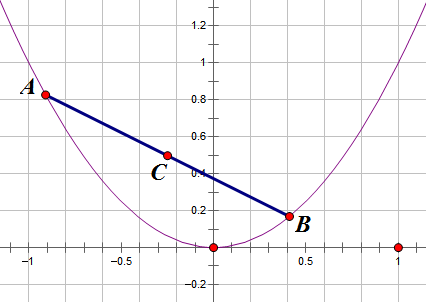
抛物线内一根定长的弦
By 苏剑林 | 2012-06-30 | 40543位读者 | 引用地球引力场的悬链线方程
By 苏剑林 | 2011-05-15 | 78645位读者 | 引用之前曾在《自然极值》系列文章中提到过均匀重力场下的悬链线形状问题,并且在那文章中向读者提出:在一个质点(地球)引力场中的悬链线形状会是怎么样的。说实话,提出这个问题的时候,我还不懂怎么解答这个问题,不过现在会了,回头一看,已经几个月了,时间过得真快...
与之前的思路一样,我们依旧采用的是“平衡态公理”,即总势能最小。从天体力学中我们知道,任意两个质点间的势能为$-\frac{Gm_1 m_2}{r}$。对于本题的悬链线问题,我们可以把地球放到坐标原点位置,而悬链的两个固定点分别为$(x_1,y_1)$和$(x_2,y_2)$,链的总长度为l。即
$$\int_{x_1}^{x_2} \sqrt{dx^2+dy^2}=l$$
《自然极值》系列——7.悬链线问题
By 苏剑林 | 2010-12-26 | 88933位读者 | 引用约翰与他同时代的110位学者有通信联系,进行学术讨论的信件约有2500封,其中许多已成为珍贵的科学史文献,例如同他的哥哥雅各布以及莱布尼茨、惠更斯等人关于悬链线、最速降线(即旋轮线)和等周问题的通信讨论,虽然相互争论不断,特别是约翰和雅各布互相指责过于尖刻,使兄弟之间时常造成不快,但争论无疑会促进科学的发展,最速降线问题就导致了变分法的诞生。
有意思的是,1690年约翰·伯努利的哥哥雅可比·伯努利曾提出过悬链线问题向数学界征求答案。即:
固定项链的两端,在重力场中让它自然垂下,求项链的曲线方程.
吊桥上方的悬垂钢索,挂着水珠的蜘蛛网,电杆间的电线都是悬链线。伽利略最早注意到悬链线,猜测悬链线是抛物线。1691年莱布尼兹、惠更斯以及约翰·伯努利各自得到正确答案,所用方法是诞生不久的微积分。
《自然极值》系列——3.平衡态公理
By 苏剑林 | 2010-11-28 | 22308位读者 | 引用光学定律无疑是一个美妙的原理,而自然界中还存在另外一个我们随处可见的“公理”。平时的生活中,我们总能看见“水往低处流”的现象,这是因为水处于地球重力场的结果(也正因为如此,某些轻生者的自杀活动才得以顺利进行;当然,我们并不需要为了验证这一点而亲自试验。)。由此我们可以联想到一个名词:重力势能。“水往低处流”意味着什么呢?高度变低了。高度更低意味着什么呢?重力势能降低了!换句话说,自然界中物体有趋于势能最低的倾向。我们可以从这个角度来解释:体系总有趋于稳定的倾向,而拥有的能量(势能)越高,则越不稳定。











最近评论