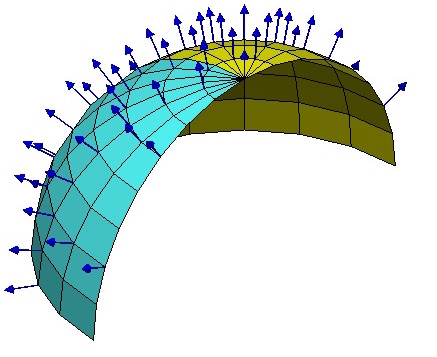
【理解黎曼几何】5. 黎曼曲率
By 苏剑林 | 2016-10-18 | 51019位读者 | 引用现在我们来关注黎曼曲率。总的来说,黎曼曲率提供了一种方案,让身处空间内部的人也能计算自身所处空间的弯曲程度。俗话说,“不识庐山真面目,只缘身在此山中”,还有“当局者迷,旁观者清”,等等,因此,能够身处空间之中而发现空间中的弯曲与否,是一件很了不起的事情,就好像我们已经超越了我们现有的空间,到了更高维的空间去“居高临下”那样。真可谓“心有多远,路就有多远,世界就有多远”。
如果站在更高维空间的角度看,就容易发现空间的弯曲。比如弯曲空间中有一条测地线,从更高维的空间看,它就是一条曲线,可以计算曲率等,但是在原来的空间看,它就是直的,测地线就是直线概念的一般化,因此不可能通过这种途径发现空间的弯曲性,必须有一些迂回的途径。可能一下子不容易想到,但是各种途径都殊途同归后,就感觉它是显然的了。
怎么更好地导出黎曼曲率来,使得它能够明显地反映出弯曲空间跟平直空间的本质区别呢?为此笔者思考了很长时间,看了不少参考书(《引力与时空》、《场论》、《引力论》等),比较了几种导出黎曼曲率的方式,简要叙述如下。
【理解黎曼几何】4. 联络和协变导数
By 苏剑林 | 2016-10-16 | 67917位读者 | 引用向量与联络
当我们在我们的位置建立起自己的坐标系后,我们就可以做很多测量,测量的结果可能是一个标量,比如温度、质量,这些量不管你用什么坐标系,它都是一样的。当然,有时候我们会测量向量,比如速度、加速度、力等,这些量都是客观实体,但因为测量结果是用坐标的分量表示的,所以如果换一个坐标,它的分量就完全不一样了。
假如所有的位置都使用同样的坐标,那自然就没有什么争议了,然而我们前面已经反复强调,不同位置的人可能出于各种原因,使用了不同的坐标系,因此,当我们写出一个向量$A^{\mu}$时,严格来讲应该还要注明是在$\boldsymbol{x}$位置测量的:$A^{\mu}(\boldsymbol{x})$,只有不引起歧义的情况下,我们才能省略它。
到这里,我们已经能够进行一些计算,比如$A^{\mu}$是在$\boldsymbol{x}$处测量的,而$\boldsymbol{x}$处的模长计算公式为$ds^2 = g_{\mu\nu} dx^{\mu} dx^{\nu}$,因此,$A^{\mu}$的模长为$\sqrt{g_{\mu\nu} A^{\mu}A^{\nu}}$,它是一个客观实体。
【理解黎曼几何】3. 测地线
By 苏剑林 | 2016-10-15 | 50399位读者 | 引用测地线
黎曼度量应该是不难理解的,在微分几何的教材中,我们就已经学习过曲面的“第一基本形式”了,事实上两者是同样的东西,只不过看待问题的角度不同,微分几何是把曲面看成是三维空间中的二维子集,而黎曼几何则是从二维曲面本身内蕴地研究几何问题。
几何关心什么问题呢?事实上,几何关心的是与变换无关的“客观实体”(或者说是在变换之下不变的东西),这也是几何的定义。根据Klein提出的《埃尔朗根纲领》,几何就是研究在某种变换(群)下的不变性质的学科。如果把变换局限为刚性变换(平移、旋转、反射),那么就是欧式几何;如果变换为一般的线性变换,那就是仿射几何。而黎曼几何关心的是与一切坐标都无关的客观实体。比如说,我有一个向量,方向和大小都确定了,在直角坐标系是$(1, 1)$,在极坐标系是$(\sqrt{2}, \pi/4)$,虽然两个坐标系下的分量不同,但它们都是指代同一个向量。也就是说向量本身是客观存在的实体,跟所使用的坐标无关。从代数层面看,就是只要能够通过某种坐标变换相互得到的,我们就认为它们是同一个东西。
因此,在学习黎曼几何时,往“客观实体”方向思考,总是有益的。
有了度规,可以很自然地引入“测地线”这一实体。狭义来看,它就是两点间的最短线——是平直空间的直线段概念的推广(实际的测地线不一定是最短的,但我们先不纠结细节,而且这不妨碍我们理解它,因为测地线至少是局部最短的)。不难想到,只要两点确定了,那么不管使用什么坐标,两点间的最短线就已经确定了,因此这显然是一个客观实体。有一个简单的类比,就是不管怎么坐标变换,一个函数$f(x)$的图像极值点总是确定的——不管你变还是不变,它就在那儿,不偏不倚。
【理解黎曼几何】2. 从勾股定理到黎曼度量
By 苏剑林 | 2016-10-14 | 66066位读者 | 引用黎曼度量
几何,英文名是Geometry,原意是大地测量。既然是测量,就必须有参考物,还有得知道如何计算距离。
有了参照物,我们就可以建立坐标系,把每个点的坐标都写下来,至于计算距离,我们有伟大的勾股定理:
$$ds^2 = dx^2 + dy^2 \tag{1} $$
但这里我们忽略了两个问题。
第一个问题是,我们不一定使用直角坐标系,如果使用极坐标,那么应该是
$$ds^2 = dr^2 + r^2 d\theta^2 \tag{2} $$
因此可以联想,最一般的形式应该是
$$ds^2 = E(x^1, x^2)(dx^1)^2 + 2F(x^1, x^2)dx^1 dx^2 + G(x^1, x^2)(dx^2)^2 \tag{3} $$
这里的$x^1,x^2$是广义坐标,使用上标而不是下标来标记序号,是为了跟传统的教材记号一致。那这公式是什么意思呢?其实很简单,正如我们没理由要求全世界都使用人民币一样,我们没必要要求世界各地都使用同一个坐标系,而更合理的做法是,每一处地方都使用自己的坐标系(局部坐标系),然后给出当地计算距离的方法。因此,上述公式正是说,在位置$(x^1, x^2)$处计算向量$(dx^1, dx^2)$的长度的公式(当地的勾股定理)是$ds^2 = E(x^1, x^2)(dx^1)^2 + 2F(x_1, x_2)dx^1 dx^2 + G(x^1, x^2)(dx^2)^2$。
【理解黎曼几何】1. 一条几何之路
By 苏剑林 | 2016-10-14 | 75706位读者 | 引用一个月没更新了,这个月花了不少时间在黎曼几何的理解方面,有一些体会,与大家分享。记得当初孟岩写的《理解矩阵》,和笔者所写的《新理解矩阵》,读者反响都挺不错的,这次沿用了这个名称,称之为《理解黎曼几何》。
黎曼几何是研究内蕴几何的几何分支。通俗来讲,就是我们可能生活在弯曲的空间中,比如一只生活在二维球面的蚂蚁,作为生活在弯曲空间中的个体,我们并没有足够多的智慧去把我们的弯曲嵌入到更高维的空间中去研究,就好比蚂蚁只懂得在球面上爬,不能从“三维空间的曲面”这一观点来认识球面,因为球面就是它们的世界。因此,我们就有了内蕴几何,它告诉我们,即便是身处弯曲空间中,我们依旧能够测量长度、面积、体积等,我们依旧能够算微分、积分,甚至我们能够发现我们的空间是弯曲的!也就是说,身处球面的蚂蚁,只要有足够的智慧,它们就能发现曲面是弯曲的——跟哥伦布环球航行那样——它们朝着一个方向走,最终却回到了起点,这就可以断定它们自身所处的空间必然是弯曲的——这个发现不需要用到三维空间的知识。
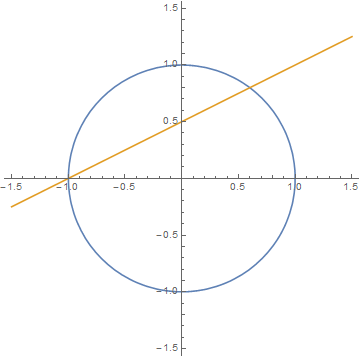
你所没有思考过的平行线问题
By 苏剑林 | 2015-03-17 | 30690位读者 | 引用本文的主题是平行线,了解数学的朋友可能会想我会写有关非欧几何的内容。但这次不是,本文的内容纯粹是我们从小就开始学习的欧氏几何,基于“欧几里得第五公设”(又称平行公设)。但即便是从小就学习的欧氏几何中的平行线,也许里边的很多问题我们都没有思考清楚。因为平行是几何中非常基本的情形,因此,在讨论这种基本命题的时候,相当容易会出现循环论证、甚至本末倒置的情况。
我们从初中开始就被灌输“同位角相等,两直线平行”、“内错角相等,两直线平行”之类的平行线判断法则,当然,还少不了的是“过直线外一点只能作一条直线与已知直线平行”。但是,这些内容之中,有多少是基本的公理,有多少是可以证明的,该如何证明,我想很多人都理解不清楚,我自己也没有一个很好的答案。那些在初中教授平行线的老师们,估计也没多少个能够把它说清楚的。后来我发现,我居然不会证明“同位角相等,两直线平行”,“欧几里得第五公设”好像并没有告诉我们这个判定法则呀。于是,我翻看了一下初中的数学教科书,发现原来当初“同位角相等,两直线平行”这一判定法则是不加证明地让我们接受的,无怪乎我怎么也想不到关于这一法则的简单的证明...
于是,我想写这篇文章,为大家理解平行线的整个逻辑提供一点参考。
从费马大定理谈起(十二):再谈谈切线法
By 苏剑林 | 2014-10-25 | 22046位读者 | 引用首先谈点题外话,关于本系列以及本博客的写作。其实本博客的写作内容,代表了笔者在这段时间附近的研究成果。也就是说,我此时在写这篇文章,其实表明我这段时间正在研究这个问题。而接下来的研究是否有结果,有怎样的结果,则是完全不知道的。所以,我在写这篇文章的时候,并不确定下一篇文章会写些什么。有些类似的话题,我会放在同一个系列去写。但不管怎样,这些文章可能并不遵循常规的教学或者学习思路,有些内容还可能与主流的思想方法有相当出入,请读者见谅,望大家继续支持!
上一篇我们谈到了切线法来求二次和三次曲线的有理点。切线法在寻找不高于三次的曲线上的有理点是很成功的,可是对于更高次的曲线有没有类似的方法呢?换句话说,有没有推广的可能性。我们从纯代数的角度来回复一下切线法生效的原因。切线法,更一般的是割线法,能够起作用,主要是因为如果有理系数的三次方程有两个有理数的根,那么第三个根肯定是有理数。如果只有一个已知的有理根,那么就可以让两个根重合为已知的那个根,从而割线变成了切线。
从费马大定理谈起(十一):有理点与切割线法
By 苏剑林 | 2014-10-24 | 22779位读者 | 引用我们在这个系列的文章之中,探索了一些有关环和域的基本知识,并用整环以及唯一分解性定理证明了费马大定理在n=3和n=4时的情形。使用高斯整数环或者艾森斯坦整数环的相关知识,相对而言是属于近代的比较“高端”的代数内容(高斯生于1777年,艾森斯坦生于1823年,然而艾森斯坦英年早逝,只活到了1852年,高斯还活到了1855年。)。如果“顺利”的话,我们可以用这些“高端”的工具证明解的不存在性,或者求出通解(如果有解的话)。
然而,对于初等数论来讲,复数环和域的知识的门槛还是有点高了。其次,环和域是一个比较“强”的工具。这里的“强”有点“强势”的意味,是指这样的意思:如果它成功的话,它能够“一举破城”,把通解都求出来(或者证明解的不存在);如果它不成功的话,那么往往就连一点非平凡的解都求不出来。可是,有些问题是求出一部分解都已经很困难了,更不用说求出通解了(我们以后在研究$x^4+y^4 = z^4 + w^4 $的整数解的时候,就能深刻体会这点。)。因此,对于这些问题,单纯用环域的思想,很难给予我们(至少一部分)解。(当然,问题是如何才算是“单纯”,这也很难界定。这里的评论是比较粗糙的。)










最近评论